创建Chrome的快捷方式,可以放在桌面,想用时双击就可以打开网页,比书签(brookmark)结构化管理更方便。
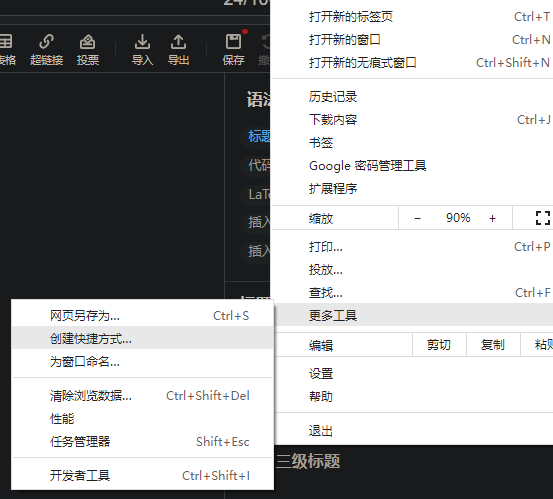
但是,安装一时爽,卸载有问题。
如果用 windows 控制面板\所有控制面板项\程序和功能 卸载,那么桌面的快捷链接会删除,但是 控制面板\所有控制面板项\程序和功能 中仍然有安装记录。(重启/重新删除均没用)

那是因为注册表(regedit)中的安装记录没删除
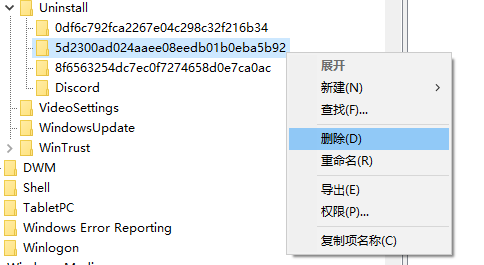
计算机\HKEY_CURRENT_USER\SOFTWARE\Microsoft\Windows\CurrentVersion\Uninstall\
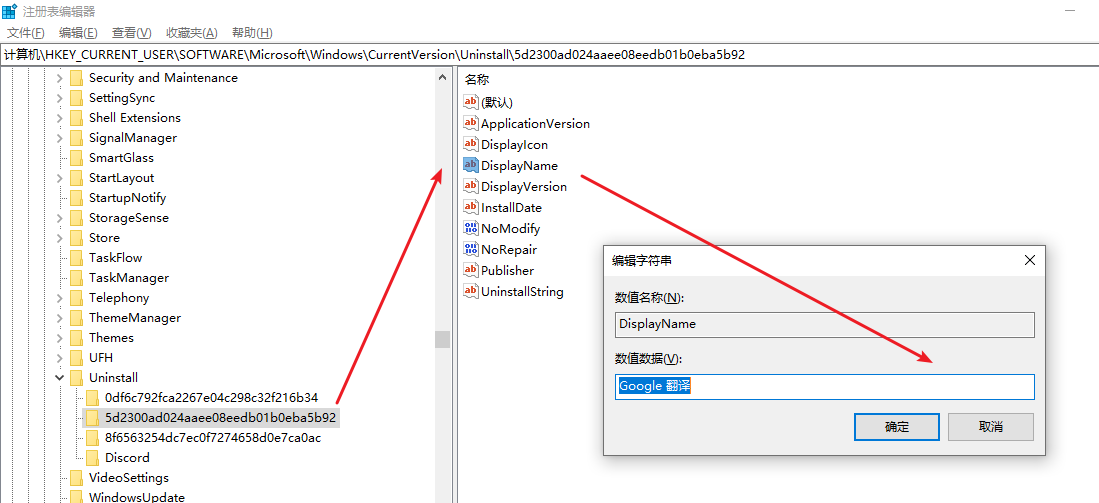
找到你想删除的项目,直接右键》删除即可