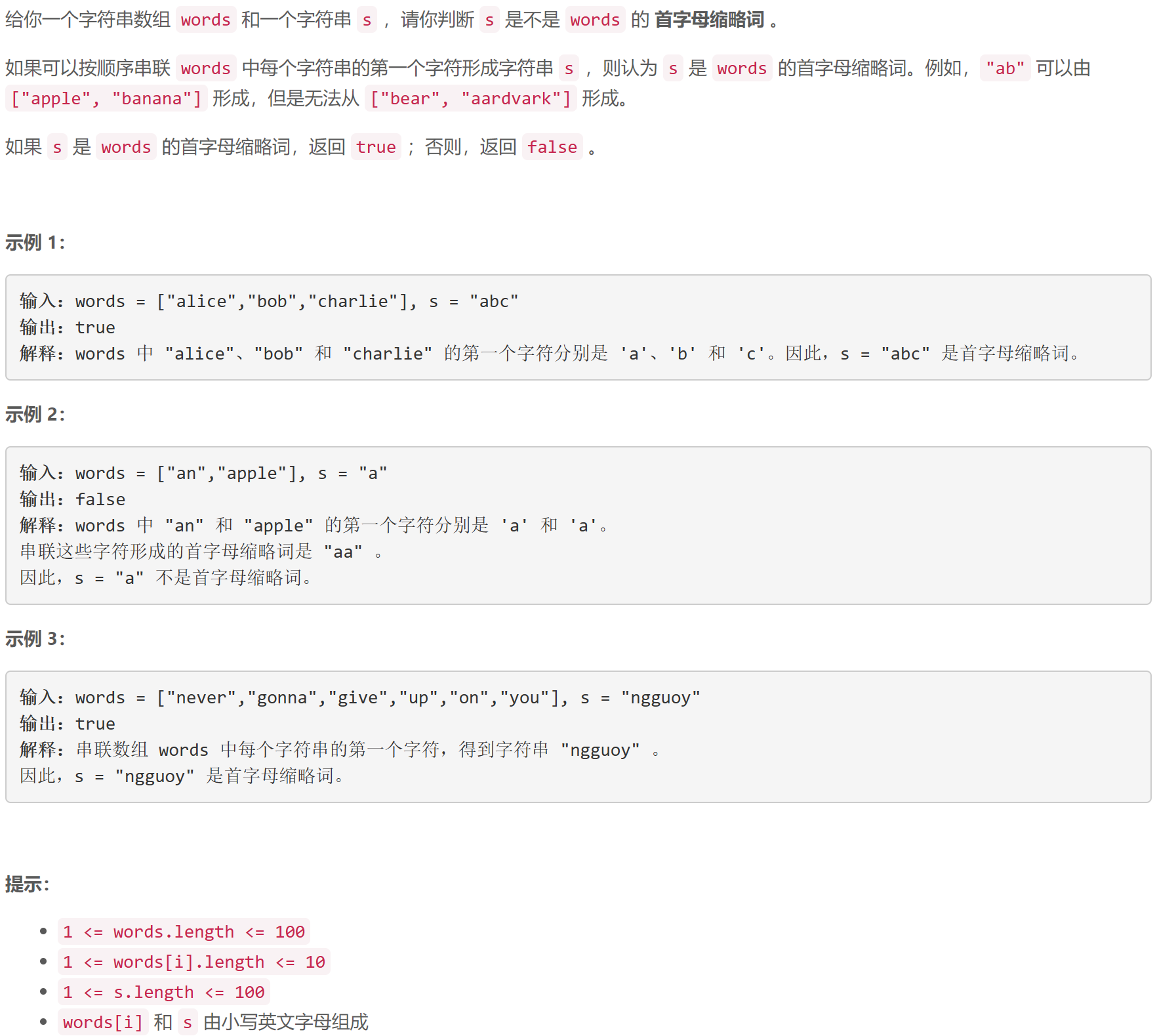
签到题…

class Solution {
public:bool isAcronym(vector<string> &words, string s) {string pf;for (auto &s: words)pf.push_back(s[0]);return pf == s;}
};

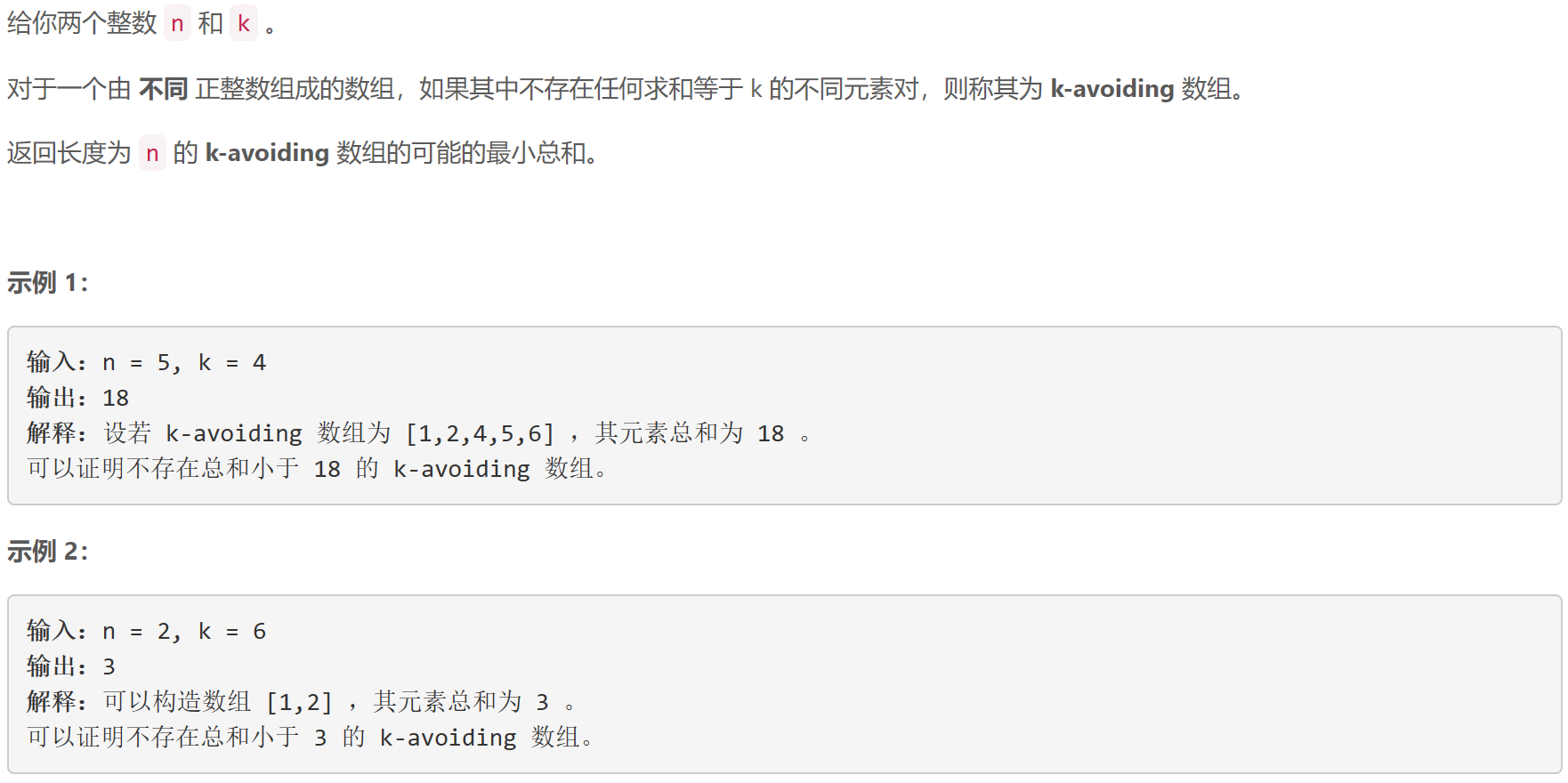
贪心：从$1$开始升序枚举，判断当前数是否可以放入数组，同时维护当前数组中的数，直到找到$n$个数。

class Solution {
public:int minimumSum(int n, int k) {set<int> vis;int s = 0;for (int i = 1; vis.size() < n; i++) {if (vis.count(k - i))continue;vis.insert(i);s += i;}return s;}
};

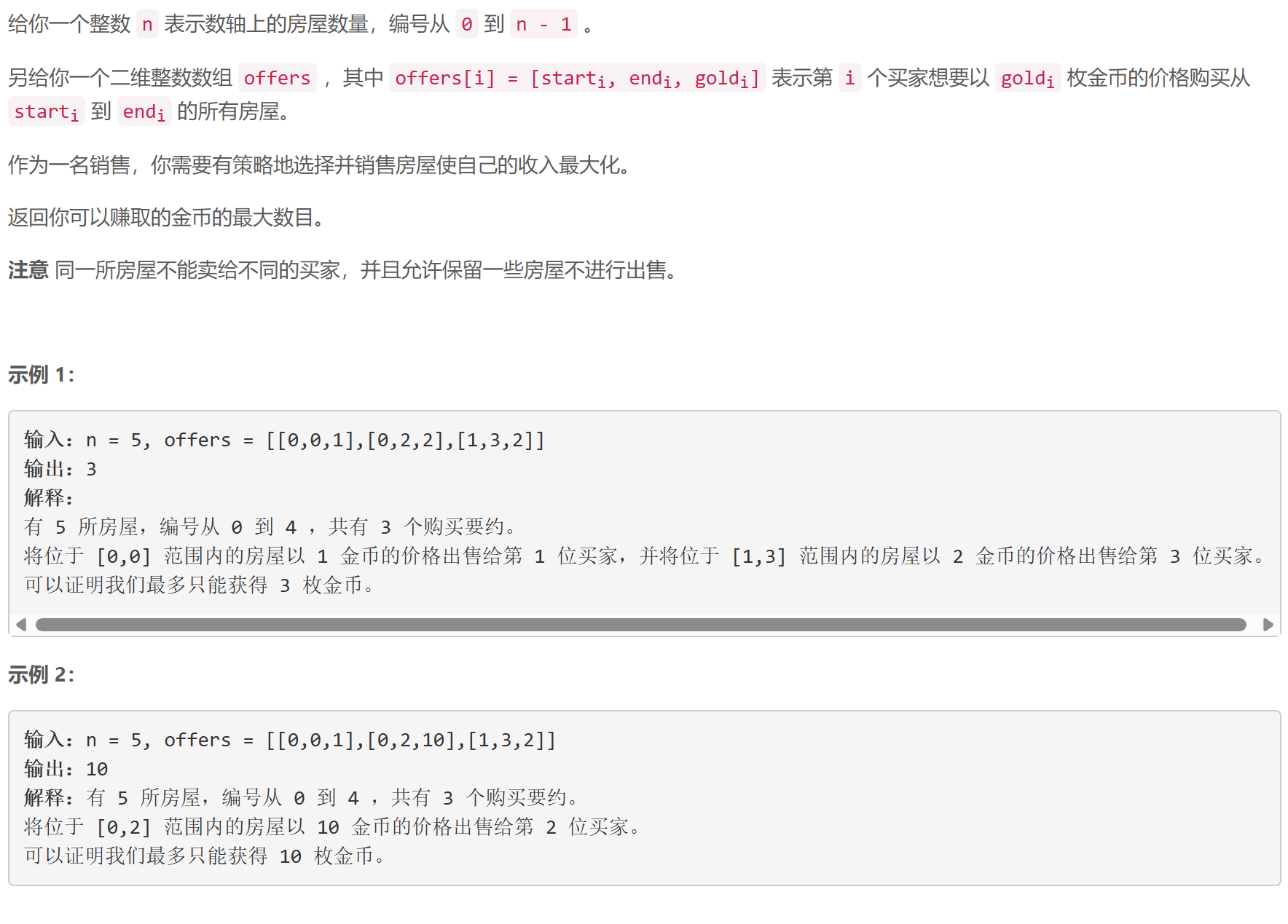
动态规划+树状数组：首先将$offers$按$star{t}_i$升序排序，枚举$offers$中的元素，设$p[i]$为销售的最右区间的右端点为$i$的情况下能够得到的最大利润，设当前元素为$[l,r,g]$，则可以更新状态： p [ r ] = m a x { p [ r ] m a x { p [ k ] ∣ 0 ≤ k ≤ l − 1 } + g p[r]=max\left\{\begin{matrix} p[r] \\ max\{p[k] \;|\; 0\le k \le l-1 \} + g \end{matrix}\right. p[r]=max{p[r]max{p[k]∣0≤k≤l−1}+g​
利用树状数组来维护前缀上的极大值。

class Solution {
public:int maximizeTheProfit(int n, vector<vector<int>> &offers) {N = n + 5;a = vector<int>(N, 0);sort(offers.begin(), offers.end());int res = 0;for (auto &it: offers) {int l = it[0] + 1, r = it[1] + 1, g = it[2];//树状数组中下标从1开始int cur = query(l - 1) + g;//查询前缀极大值res = max(res, cur);update(r, cur); //树状数组更新}return res;}int N;vector<int> a;//树状数组inline int lowbit(int x) {return x & -x;}void update(int loc, int val) {// li[loc]=max(li[loc], val);for (; loc < N; loc += lowbit(loc))a[loc] = max(a[loc], val);}int query(int loc) {// max{li[k] | 1<=k<=loc}int res = 0;for (; loc > 0; loc -= lowbit(loc))res = max(res, a[loc]);return res;}
};

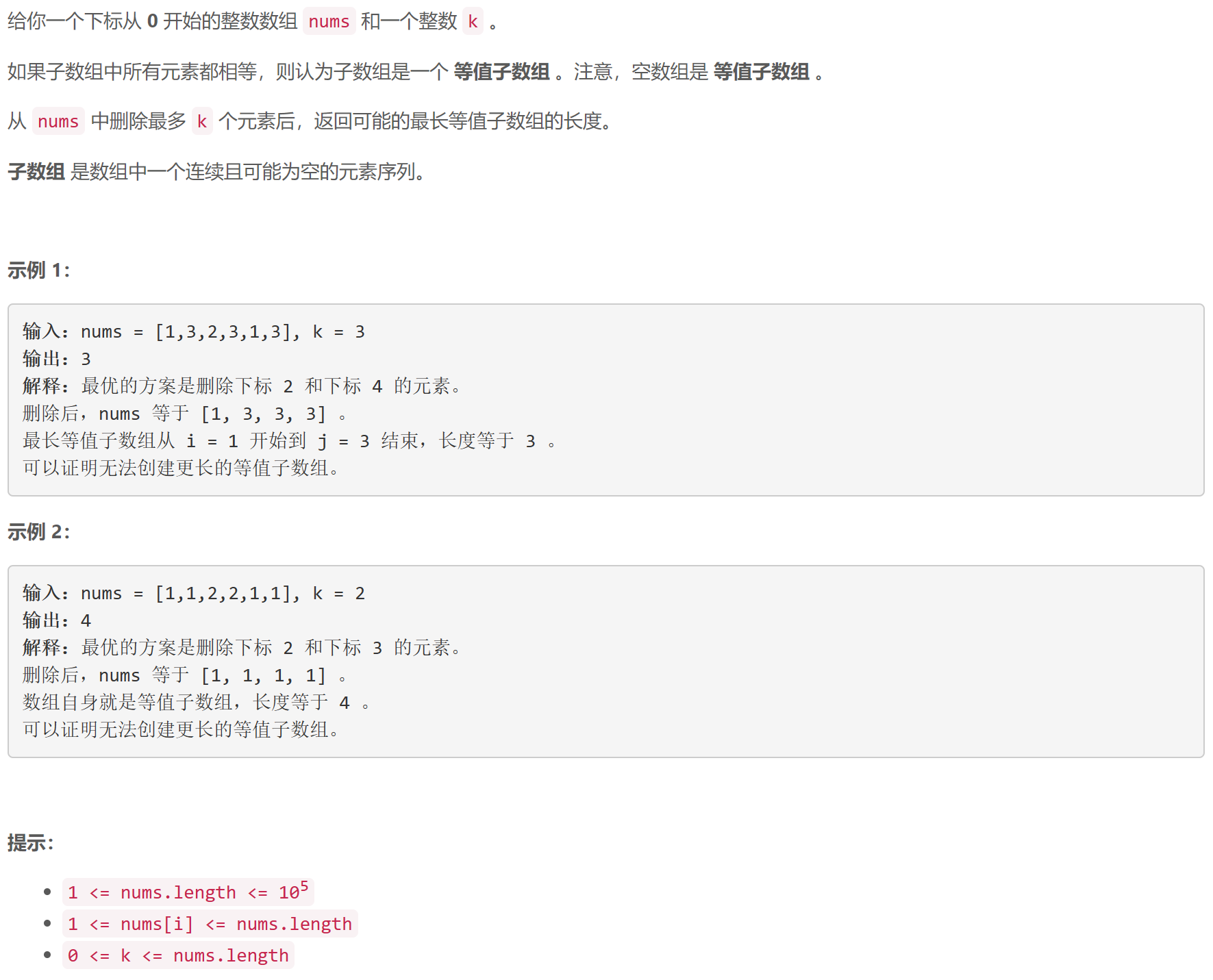
二分+哈希：用二分查找答案 $len$，这样问题就变成了：判断从 $nums$ 中删除最多 $k$ 个元素后，是否存在长为 $len$ 的等值子数组。设$loc[v]$为$nums$中所有$v$所在下标组成的升序数组，若存在 $0\le i\le i+len-1<loc[v].size()$ 使得 $loc[v][i+len-1]-loc[v][i]+1-len\le k$，则说明可以得到长为 $len$ 的值为$v$的等值子数组，枚举$nums$中不同的数，即可判断是否可以得到长为 $len$ 的等值子数组。

class Solution {
public:int longestEqualSubarray(vector<int> &nums, int k) {int n = nums.size(), l = 1, r = n;unordered_map<int, vector<int>> loc;for (int i = 0; i < n; i++)loc[nums[i]].push_back(i);auto can = [&](int len) {//判断是否可以得到长为len的等值子数组int find = 0;for (auto &[_, vec]: loc) {//枚举不同的数for (int i = 0; i + len - 1 < vec.size(); i++)if (vec[i + len - 1] - vec[i] + 1 - len <= k)return true;}return false;};while (l < r) {//二分查找答案int mid = (l + r + 1) / 2;if (can(mid))l = mid;elser = mid - 1;}return l;}
};