分类预测 | MATLAB实现NGO-DBN北方苍鹰优化深度置信网络多特征输入分类预测

效果一览

基本介绍

MATLAB实现NGO-DBN北方苍鹰优化深度置信网络多特征输入分类预测
多特征输入单输出的二分类及多分类模型。程序内注释详细，直接替换数据就可以用。程序语言为matlab，程序可出分类效果图，迭代优化图，混淆矩阵图。
北方苍鹰优化学习率、迭代次数和隐藏层单元数目。

深度信念网络，DBN，Deep Belief Nets，神经网络的一种。既可以用于非监督学习，类似于一个自编码机；也可以用于监督学习，作为分类器来使用。DBN由若干层神经元构成，组成元件是受限玻尔兹曼机（RBM）。
RBM是一种神经感知器，由一个显层和一个隐层构成，显层与隐层的神经元之间为双向全连接。限制玻尔兹曼机和玻尔兹曼机相比，主要是加入了“限制”。限制玻尔兹曼机可以用于降维（隐层少一点），学习特征（隐层输出就是特征），深度信念网络（多个RBM堆叠而成）等。

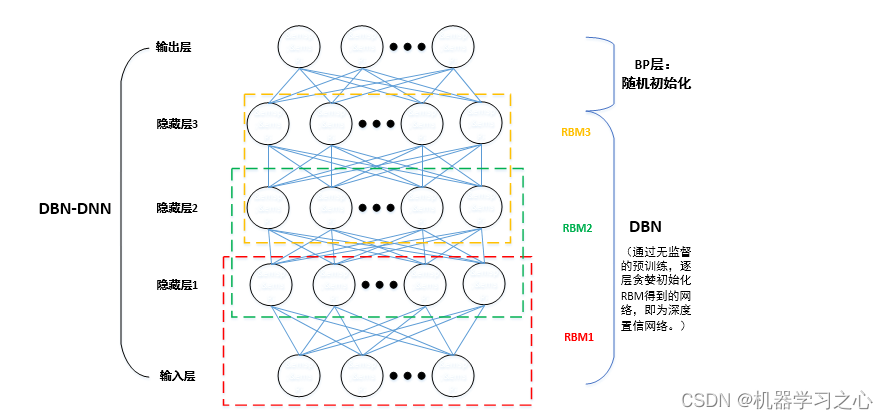
模型描述

受限玻尔兹曼机（RBM）是一种具有随机性的生成神经网络结构，它本质上是一种由具有随机性的一层可见神经元和一层隐藏神经元所构成的无向图模型。它只有在隐藏层和可见层神经元之间有连接，可见层神经元之间以及隐藏层神经元之间都没有连接。并且，隐藏层神经元通常取二进制并服从伯努利分布，可见层神经元可以根据输入的类型取二进制或者实数值。

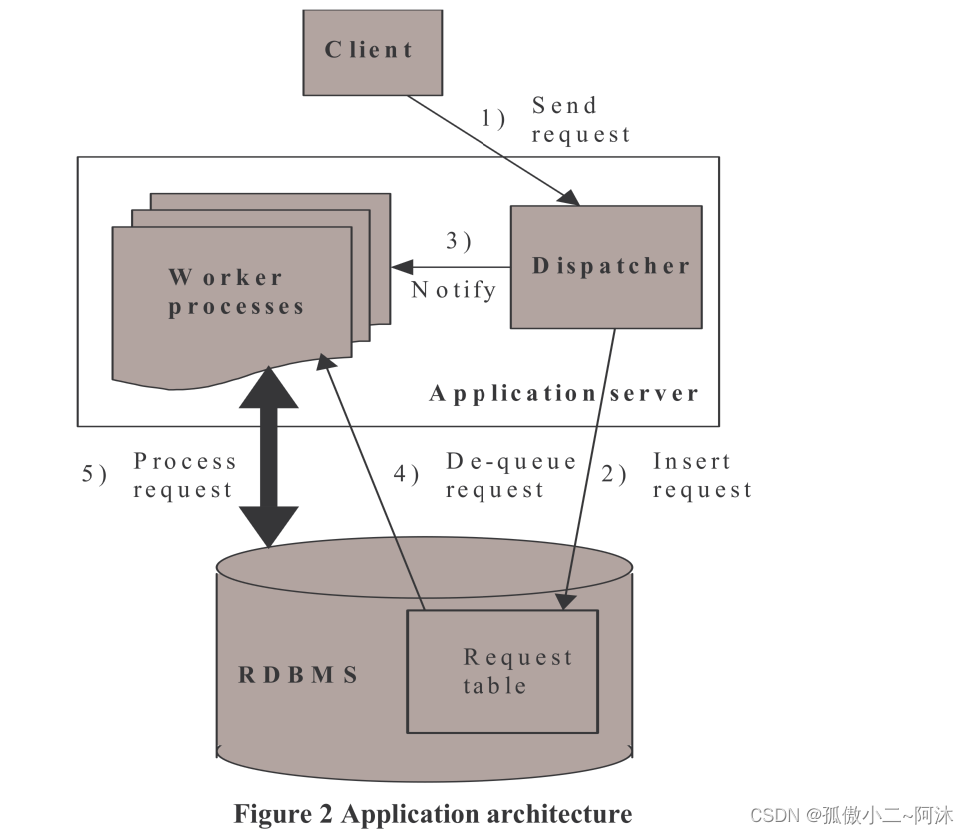
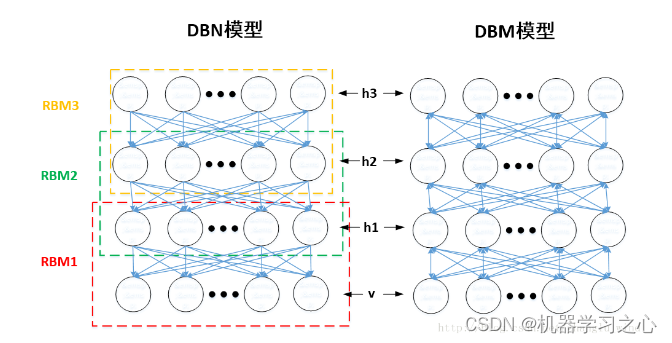
• 既然提到了受限玻尔兹曼机（RBM），就不得不说一下，基于RBM构建的两种模型：DBN和DBM。如图二所示，DBN模型通过叠加RBM进行逐层预训练时，某层的分布只由上一层决定。例如，DBN的v层依赖于h1的分布，h1只依赖于h2的分布，也就是说，h1的分布不受v的影响，确定了v的分布，h1的分布只由h2来确定。而DBM模型为无向图结构。
• 也就是说，DBM的h1层是由h2层和v层共同决定的，它是双向的。如果从效果来看，DBM结构会比DBN结构具有更好的鲁棒性，但是其求解的复杂度太大，需要将所有的层一起训练，不太利于应用。而DBN结构，如果借用RBM逐层预训练的方法，就方便快捷了很多，便于应用，因此应用的比较广泛。

程序设计

• 完整源码和数据下载方式（资源处直接下载）：Matlab实现NGO-DBN北方苍鹰优化深度置信网络多特征输入分类预测（完整源码和数据）

%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%%  清空环境变量
clc;
clear;
warning off
close all
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%%  添加路径
addpath("Toolbox\")
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%%  读取数据
res = xlsread('数据集.xlsx');%%  分析数据
num_class = length(unique(res(:, end)));  % 类别数（Excel最后一列放类别）
num_res = size(res, 1);                   % 样本数（每一行，是一个样本）
num_size = 0.7;                           % 训练集占数据集的比例%%  损失函数曲线
figure
plot(1: length(accu), accu, 'r-', 'LineWidth', 1)
xlabel('迭代次数')
ylabel('准确率')
legend('训练集正确率')
title ('训练集正确率曲线')
xlim([1, length(accu)])
gridfigure
plot(1 : length(loss), loss, 'b-', 'LineWidth', 1)
xlabel('迭代次数')
ylabel('损失函数')
legend('训练集损失值')
title ('训练集损失函数曲线')
xlim([1, length(loss)])
grid%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%%  混淆矩阵
if flag_conusion == 1figurecm = confusionchart(T_train, T_sim1);cm.Title = 'Confusion Matrix for Train Data';cm.ColumnSummary = 'column-normalized';cm.RowSummary = 'row-normalized';figurecm = confusionchart(T_test, T_sim2);cm.Title = 'Confusion Matrix for Test Data';cm.ColumnSummary = 'column-normalized';cm.RowSummary = 'row-normalized';
end

参考资料

[1] https://download.csdn.net/download/kjm13182345320/87899283?spm=1001.2014.3001.5503
[2] https://download.csdn.net/download/kjm13182345320/87899230?spm=1001.2014.3001.5503