二叉树的种类

最优二叉树

最优二叉树画法
- 排序
- 取最小两个值和,得到新值加入排序
- 重复1,2
前序、中序和后序遍历是树形数据结构(如二叉树)中常用的遍历方式,用于按照特定顺序遍历树的节点。这些遍历方式在不同应用中有不同的用途。

以下是这些遍历方式的解释:
1. 前序遍历(Preorder Traversal):
- 从根节点开始,按照「根节点 - 左子树 - 右子树」的顺序遍历树的节点。
- 对于每个节点,先访问该节点,然后递归遍历左子树,最后递归遍历右子树。
- 前序遍历可以用于复制整棵树。
函数方法:
void PREORDER(bitree *r)
{if(r==NULL) return;//空树返回printf("%c",r->data); //先访问当前节点PREORDER(r->lchild); //再访问该节点的左子树PREORDER(r->rchild); //最后访问该节点右子树
}图像法: 看穿过环的顺序,确定前序遍历的顺序。

2. 中序遍历(Inorder Traversal):
- 从根节点开始,按照「左子树 - 根节点 - 右子树」的顺序遍历树的节点。
- 对于每个节点,先递归遍历左子树,然后访问该节点,最后递归遍历右子树。
- 中序遍历在二叉搜索树中得到的结果是有序的。
void INORDER(bitree *r)
{if(r==NULL) return;//空树返回INORDER(r->lchild); //先访问该节点的左子树printf("%c",r->data); //再访问当前节点INORDER(r->rchild); //最后访问该节点右子树
}图像法: 看穿过环的顺序,确定中序遍历的顺序。

3. 后序遍历(Postorder Traversal):
- 从根节点开始,按照「左子树 - 右子树 - 根节点」的顺序遍历树的节点。
- 对于每个节点,先递归遍历左子树,然后递归遍历右子树,最后访问该节点。
- 后序遍历常用于内存回收或资源释放等操作。
void POSTORDER(bitree *r)
{if(r==NULL) return;//空树返回POSTORDER(r->lchild); //先访问该节点的左子树POSTORDER(r->rchild); //最后访问该节点右子树printf("%c",r->data); //再访问当前节点} 图像法: 看穿过环的顺序,确定后序遍历的顺序。 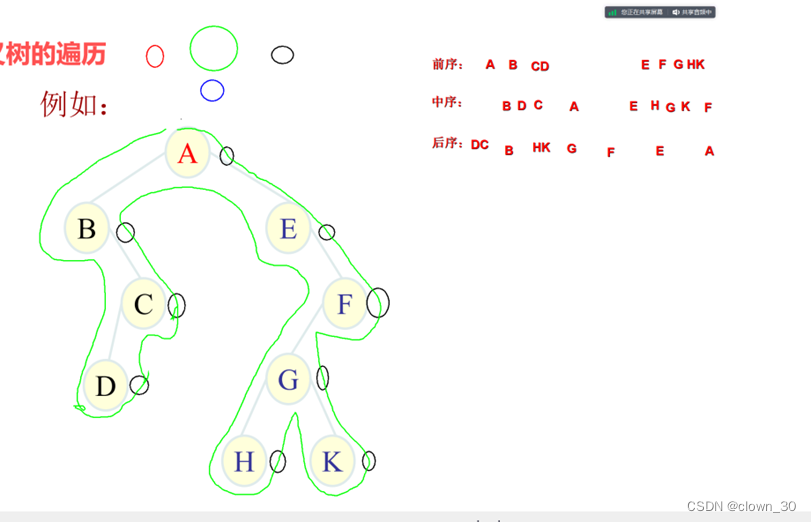
这些遍历方式都是深度优先遍历(Depth-First Traversal)的一种。深度优先遍历从根节点开始,尽可能深地访问树的分支,然后再回溯到其他分支。与之相对的是广度优先遍历(Breadth-First Traversal),它从根节点开始,按层级遍历树的节点。