博客中所有内容均来源于自己学习过程中积累的经验以及对yalmip官方文档的翻译：https://yalmip.github.io/tutorials/

        这篇博客将详细介绍yalmip工具箱中约束条件操作相关函数的用法。

1.约束条件操作的相关函数

1.1 boundingbox函数

        boundingbox函数用于求出一组约束条件中所包含变量的上下限，即提取约束条件中变量的显式边界，使用语法如下：

[B,L,U] = boundingbox(Constraint,options,x)

        其中，Constraint表示约束条件(必要输入)，options表示Yalmip设置(可选输入)，x表示需要提取边界的变量（可选输入），B为变量x的上下限约束，为lmi变量形式，L和U分别表示变量的上下限，均为矩阵形式(可选输出)，下面是一个简单的示例：

        例1：使用boundingbox求出约束x²+y²<=4中变量的上下界，并画图展示

sdpvar x y
Ball = x^2+y^2 <= 4;
[Box,L,U] = boundingbox(Ball);
plot(Box,[x y]);
hold on
plot(Ball,[x y],'y')

        运行结果：

 图1 boundingbox函数效果展示

L =

   -2.0000

   -2.0000

U =

    2.0000

    2.0000

        光看上面的例子，可能很难体会到这个函数的作用，但其实这个函数在求解优化问题时是非常有用的。我们知道在求解优化问题的过程中，经常会有非线性项，需要用到大M法将其转为线性项，这时候如果可以确定变量的边界，将会非常有效地提高优化问题求解效率，下面进行举例说明：

例2：有1个0-1变量x和1个大于0的连续变量y相乘，使用大M法将其线性化。

        引入大于0的连续辅助变量z=xy，可以使用变量z和3个辅助约束条件代替这个非线性项：

        z≤Mx，z≤y，z≥y-M(1-x)

        其中M是变量y的一个上界，下面分析一下两者是否等效：

        1)当x=0时，由z=xy可得z=0，由z≤Mx和z≥0同样可得z=0，两者等效；

        2)当x=1时，由z=xy可得z=y，由z≤Mx，z≤y，z≥y-M(1-x)可得z≤y且z≥y，即z=y，两者仍然等效。

        但在实际使用时，M的取值不能太大也不能太小，如果M取值太大，可能会因为浮点数精度的问题造成约束的偏差，也扩大了约束的范围，降低求解效率；如果M取值太小，甚至小于变量y的上界，那可能会改变变量y的取值范围，甚至导致模型不可解(例如，变量y∈[0,100]，M取了50，那么约束z≤Mx会将y的范围限制在[0,50]之间，改变了y的取值范围)。

        因此，M最合适的取值就是y的上限，使用boundingbox函数可以方便的求出变量的上界，这就是其作用所在：求出变量的上界之后，如果Yalmip建模时用到了大M法，将会自动使用变量的上界进行等效转换。

1.2 chebyball函数

        chebyball函数用于求解一组约束条件所限定的边界中最大的内切圆(如果有3个或以上的变量，就是内切球以及内切超球体)，其基本语法如下：

[xc,r] = chebyball(Constraint,options)

        其中，Constraint表示约束条件，options表示Yalmip选项，xc和r分别表示内切圆的圆心坐标和半径。举例说明如下：

例3：已知变量x和y满足约束0≤x≤1，0≤y≤1，画出该范围内最大的圆。

        代码和运行结果如下：

sdpvar x y
Box = -1 <= [x y] <= 1;
[xc,r] = chebyball(Box);
plot(Box);
hold on
plot((x-xc(1))^2 + (y-xc(2))^2 <= r^2,[],'y')

        运行结果：

图2  chebyball函数效果展示 

        例3和例1正好正好是一个逆向过程。

1.3 check函数

        check函数用在约束问题求解之后，用于检查约束条件的满足情况，其基本语法如下：

[pres,dres] = check(F)

        其中，F表示约束条件，pres和dres分别表示原始约束和对偶约束的残差，残差即为约束实际取值和约束条件边界的偏差值，当约束条件满足时，残差为正数，当约束条件不满足时，残差为负数(具体理论不做介绍，可以使用help check或者自行查找相关理论)，举例说明如下：

例4：

sdpvar x
F0 = [x == 1];
F1 = [x == 1.25];
F2 = [0.9 <= x <= 1.2];
F3 = [x >= 2];
optimize(F0);
[pres1,dres1] = check(F1);
[pres2,dres2] = check(F2);
[pres3,dres3] = check(F3);
pres1
pres2
pres3

        运行结果：

pres1 =

   -0.250

pres2 =

    0.1000

pres3 =

    -1

        x实际取值为1，约束条件F1不满足，所以残差为负数，取值为-0.25，约束条件F2满足，所以残差为正数，取值为0.1，约束条件F3不满足，所以残差为负数，取值为-1。在调试代码时check函数可以发挥很大作用。

1.4 dual函数

        dual函数用于求出与约束条件相应的对偶变量，其语法如下：

Z = dual(F)

        其中，F表示约束条件，Z表示其对偶变量的取值。由于该方法是直接获取对偶变量的取值，所以一般都需要优化问题求解成功后才可以使用。首先来看官方文档给出的例子，学习一下dual函数的用法。

例5：求解优化问题后，使用dual函数提取约束条件对应的对偶变量。

A = [-1 2;-3 -4];
P = sdpvar(2,2);
F = [P >= 0, A'*P+P*A <= 0, trace(P) == 1];
optimize(F);
Z2 = dual(F(2));

运行结果：

Z2 =

   1.0e-09 *

    0.8605   -0.1947

   -0.1947    0.0440

        求解优化问题后，使用dual函数就可以求出某个约束条件对应的对偶变量取值。由线性规划的理论可知，如果原问题具有最优解，那么当原问题取得最优解时，其对偶问题也取得最优解，且两个问题的最优目标函数相同，我们用一个例子来验证：

例6：已知一个线性规划的原问题和对偶问题，使用dual函数验证强对偶定理(即原问题的最优解和对偶问题的最优解相同)

        原问题为：

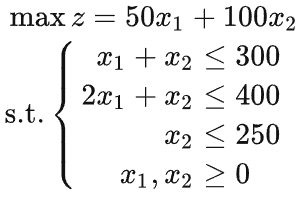
        对偶问题为： 

        matlab代码和运行结果：

sdpvar x1 x2
z = 50*x1 + 100*x2;
F = [ x1 + x2 <= 300 , ...2*x1 + x2 <= 400 , ...x2 <= 500 , x1 >= 0 , x2 >= 0];
optimize(F , -z)
y = dual(F(1:3))
z = value(z)
w = [300 400 250]*y

运行结果：

y =

   100

     0

     0

z =

       30000

w =

       30000

        由结果可知，原问题和对偶问题的最优解相等，满足强对偶定理。

1.5 hull函数

        hull函数用于求出一组约束条件的凸包(convex hull，此处不再做理论介绍，只介绍用法)，标准语法如下：

F = hull(F1,F2,...)

        其中F1，F2...表示原始的约束条件，F表示这组约束条件的凸包，官方文档中用图形直观地展示了这个函数的作用：

例7：

sdpvar x y
F1 = [-1 <= x <= 1, -1 <= y <= 1];
F2 = [-1.5 <= x-y <= 1.5, -1.5 <= x+y <= 1.5];
H = hull(F1,F2);
plot(H);hold on
plot(F2);
plot(F1);

运行结果：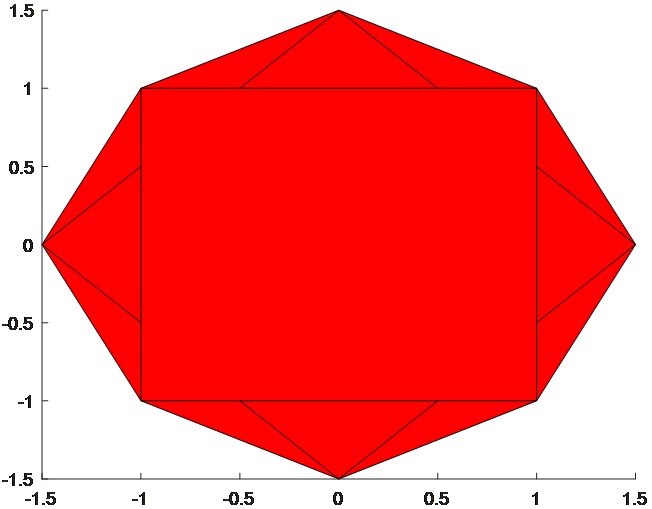

图3 约束条件和相应的convex hull 

1.6 vertex函数

        (该函数仅最新版yalmip才有，如果没有去官网下载最新版即可)vertex函数用于求出一组约束的顶点，其标准语法如下：

V = vertex(Constraint,[x])

        其中，Constraint表示约束条件，x表示决策变量，V表示顶点坐标，举例说明如下：

例8：

        二维空间：

x = sdpvar(2,1);
B = [-1 <= x <= 1, sum(x) <= 3/2];
clf
plot(B,[],[],[],sdpsettings('plot.shade',0.1));
hold on;grid on
v = vertex(B,x);
m = plot(v(1,:),v(2,:),'bo');
set(m,'Markersize',10);
set(m,'Markerface','yellow');

        三维空间：

x = sdpvar(3,1);
P = [-1 <= x <= 1, sum(abs(x)) <= 1,sum(x)>=.5]
clf
plot(P,x,[],[],sdpsettings('plot.shade',0.1));
hold on;grid on
v = vertex(P,x);
m = plot3(v(1,:),v(2,:),v(3,:),'bo');
set(m,'Markersize',10);
set(m,'Markerface','yellow');

        运行结果为：

图4 二维约束的顶点

图5 三维约束的顶点

2.调试小技巧，给约束命名

        当所求优化问题比较复杂时，有的时候很难记住每个约束在对应的约束变量中是第几个位置，调试代码时很不方便，这时候可以使用一个:加上一个字符串，就可以给约束命名，用于在约束变量中打上标记。例如：

sdpvar x
Constraints = [(x >= 0):'Positivity',(x <= 1):'Bounded']

        运行结果：

        当需要用到某个约束时，还可以用对应的’Tag’来索引，例如：

sdpvar x
Constraints = [(x >= 0):'Positivity',(x <= 1):'Bounded'];
Constraints('Bounded')

        运行结果：