本贴介绍最短路径的计算，实现方式为迪杰斯特拉算法；对于弗洛伊德算法，区别在于计算了所有结点之间的最短路径，考虑到MATLAB计算的便捷性，计算时只需要反复使用迪杰斯特拉即可，暂不介绍弗洛伊德的实现；此外，对于带有负权值的图，通过贝尔曼‐福特算法解决~

---

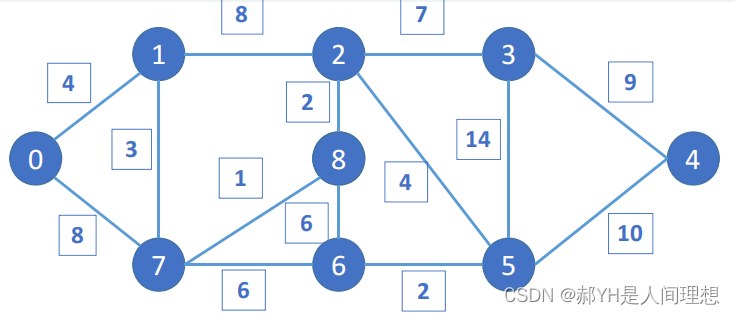
迪杰斯特拉算法的思想，通俗的归纳来说就是：从当前结点出发，寻找一个未与当前简历连接——且路径最小的点作为下一个寻找到的地址。有关结点是否建立连接，需要一个如下的矩阵来辅助记录。

 若还未建立连接，则将前驱标记为-1，距离记录为无穷~

至于Distance内，存放的是起点到当前结点的最短距离，这一距离可能会不断更新，直到寻找到最短的路径为止~

实现的具体底代码：

• 第一种：

[P,d] = shortestpath(G, 9, 4)

如上代码中，P表示的9与4节点之间最短路径经过的结点，而d保存的是最短路径值的总和~

• 第二种：

D = distances(G);
D(1,2);
D(9,4);

如上代码中，D是一个存储了任意两结点之间最短路径的矩阵，通过索引访问的方式，即可求出任意两点的最短路径~

此外，如下是计算求出指定节点指定距离内部的全部结点的实现方式：

[nodeIDs,dist] = nearest(G, 2, 10); 

 注意，上述几个函数从2017a版本后才能全部使用

如下是创建图并计算图的具体实现方式：

s = [9 9 1 1 2 2 2 7 7 6 6  5  5 4];
t = [1 7 7 2 8 3 5 8 6 8 5  3  4 3];
w = [4 8 3 8 2 7 4 1 6 6 2 14 10 9];
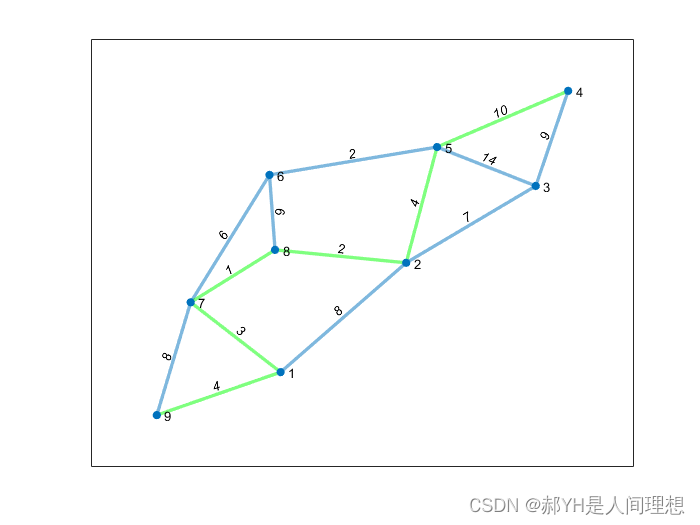
G = graph(s,t,w);

plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2) set( gca, 'XTick', [], 'YTick', [] );[P,d] = shortestpath(G, 9, 4);myplot = plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2); 
highlight(myplot, P, 'EdgeColor', 'g') ; 

结果如下，绿色即为最短路径：