0 摘要

论文：A survey on learning from imbalanced data streams: taxonomy, challenges, empirical study, and reproducible experimental framework
发表：2023年发表在Machine Learning上。
源代码：https://github.com/canoalberto/imbalanced-streams

类不平衡给数据流分类带来了新的挑战。最近在文献中提出的许多算法使用各种数据驱动层面、算法层面和集成方法来解决这个问题。然而，在如何评估这些算法方面，缺乏标准化和商定的程序和基准。本文工作提出了一个标准化、详尽和全面的实验框架，以评估各种具有挑战性的不平衡数据流场景中的算法。实验研究在515个不平衡数据流上评估了24个最先进的数据流算法，在二分类和多分类场景下这些数据流结合了静态和动态类不平衡比率、实例级困难、概念漂移、真实世界和半合成数据集。这导致了一项大规模的实验研究，比较了数据流挖掘领域中最先进的分类器。我们讨论了这些场景中最先进的分类器的优点和缺点，并为最终用户提供了针对不平衡数据流选择最佳算法的一般建议。此外，我们还制定了该领域的开放挑战和未来方向。我们的实验框架是完全可复制的，并且很容易用新方法扩展。通过这种方式，我们提出了一种标准化的方法来在不平衡的数据流中进行实验，其他研究人员可以使用这种方法来对新提出的方法进行完整、可信和公平的评估。

1 引言

我们收集、整合、存储和分析大量数据的能力最近取得了进步，这给机器学习方法带来了新的挑战。传统的算法被设计为从静态数据集中发现知识。相反，当代数据源产生的信息具有数量和速度的特点。这样的场景被称为数据流(Gama, 2010; Bahri et al., 2021; Read and Žliobaitė, 2023)，传统方法在处理这种数据流有所欠缺。

与从静态数据中学习相比，最大的挑战之一在于需要适应数据不断变化的本质，其中的概念是非平稳的，可能会随着时间而变化。这种现象被称为概念漂移(Krawczyk et al.， 2017;Khamassi et al.，2018)，并导致分类器的退化，因为在以前的概念上学习的知识可能对最近的实例不再有用。从概念漂移中恢复需要显式检测器或隐式适应机制的存在。

数据流挖掘的另一个重要挑战在于需要算法显示对类不平衡的鲁棒性(Krawczyk, 2016;Fernández et al.，2018a)。尽管经过近三十年的研究，处理倾斜的类分布仍然是机器学习的一个关键领域。这在流场景中变得更具挑战性，因为不平衡与概念漂移同时发生。不仅类的定义发生了变化，而且失衡比例也变得动态，类的角色也可能发生转换。假设固定数据属性的解决方案不能在这里应用，因为流可能在不同程度的不平衡和类之间的平衡期间振荡。

此外，不平衡的流可能有其他潜在的困难，如小样本量，边界和罕见的实例，类之间的重叠，或嘈杂的标签(Santos et al.，2022)。不平衡的数据流通常通过类重采样来处理(Korycki & Krawczyk, 2020;Bernardo等，2020b;Bernardo & Della Valle, 2021a)，算法自适应机制(Loezer et al, 2020;Lu et al, 2020)，或集成方法(Zyblewski et al, 2021;Cano & Krawczyk, 2022)。这个问题的动机是大量现实世界的问题，其中数据既存现流的特征又出现噪声的情况，例如Twitter流(Shah & Dunn, 2022)、欺诈检测(Bourdonnaye & Daniel, 2022)、滥用和仇恨言论检测(Marwa等人，2021)、物联网(Sudharsan等人，2021)或智能制造(Lee, 2018)。虽然有一些关于如何处理不平衡数据流的工作，但对于完全可复制、透明和有影响力的研究来说，没有一致认可的标准、基准或良好实践。

研究的目标。为二元和多类不平衡数据流创建一个标准化、详尽和信息丰富的实验框架，并对最先进的分类器进行广泛的比较。

动机。虽然文献中有许多针对漂移和不平衡数据流的算法，但缺乏关于如何全面评估这些算法的标准化程序和基准。现有的研究通常局限于算法和数据困难的选择，通常只考虑二分类数据，并且没有提供必须考虑不平衡数据流的哪些方面并将其转化为有意义的基准问题的见解。不平衡数据流需要一个统一和全面的评估框架，可以作为研究人员根据文献中相关方法评估他们新提出的算法的模板。此外，对最先进的方法进行深入的实验比较，可以获得有价值的见解，了解在不同条件下分类器和学习机制的工作原理。因此，我们提出了一个评估框架，并进行了大规模的实证研究，以获得深入了解的性能方法下的广泛和不同的一组数据困难。

概述和贡献。本文提出了一个完整的框架，用于对不平衡数据流的分类器进行基准测试和评估。我们总结现有的工作，并根据既定的分类法专门针对倾斜和流问题进行组织。我们提炼出该领域中出现的最关键和最具洞察力的问题，并用它们设计一组基准问题，以捕捉独特的学习困难和挑战。我们将这些基准编译成一个框架，该框架嵌入了各种度量、统计测试和可视化工具。最后，我们通过比较24种最先进的算法来展示我们的框架，这使我们能够选择表现最好的算法，发现它们在哪些特定领域表现出色，并为最终用户制定建议。本文的主要贡献总结如下:

• 不平衡数据流的算法分类。我们根据已建立的分类法组织了目前最先进的方法，这些分类法总结了从不平衡数据流中学习的最新进展，并提供了最重要贡献的综述。
• 全面和可重复的评估框架。我们提出了一个完整的整体框架，用于评估二分类和多分类不平衡数据流的分类器，该框架将度量标准、统计测试和可视化工具标准化，用于透明和可重复的研究。
• 各种基准问题。我们制定了一组在我们的框架中使用的基准问题。我们捕获了不平衡数据流中存在的最重要和最具挑战性的问题，例如动态不平衡比率、实例级困难(边界、罕见和子概念)或类的数量。此外，我们还包括了现实世界和半合成的不平衡问题，总共产生了515个数据流基准测试。
• 最先进分类器之间的比较。我们基于提出的框架和515个基准问题，对24种最先进的流挖掘算法进行了广泛、全面和可重复的比较研究。
• 建议和公开挑战。基于详尽的实验研究结果，我们为最终用户制定了建议，以便了解性能最好的分类器的优点和缺点。此外，我们制定了从不平衡数据流中学习的公开挑战，这些挑战应该由研究人员在未来几年解决。

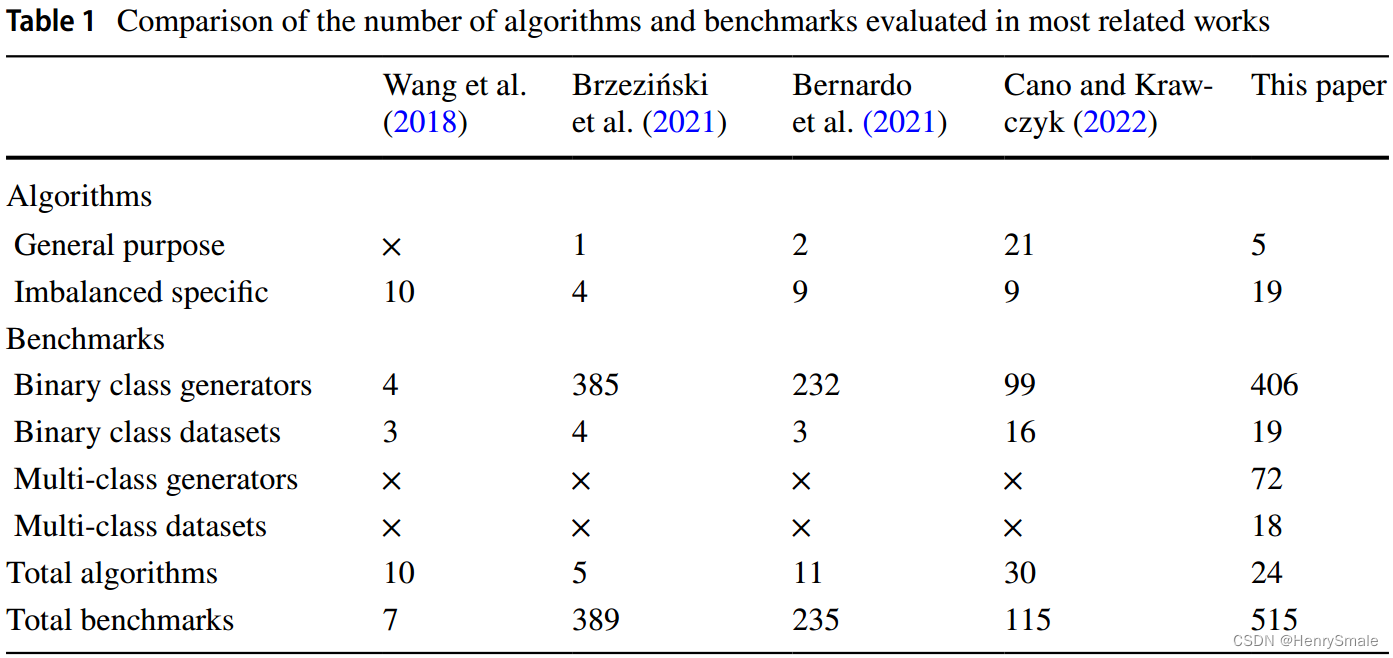
与大多数相关实验工作的比较。近年来，发表了几篇涉及类不平衡和数据流联合领域的大型实验研究的调查论文和著作。因此，重要的是要了解他们和这项工作之间的关键区别，以及我们的综述如何为这个主题提供以前的工作中没有涉及的新见解。Wang等人(2018)提出了几种现有技术的概述，包括漂移检测器和自适应分类器，并通过实验比较了它们的预测准确性。虽然是该领域的第一个专门研究，但它的局限性在于没有评估比较算法的计算复杂性，使用了非常小的数据集选择(7个基准)，并且只调查了不平衡数据流的有限属性(没有触及实例级特征或多类问题)。Brzeziński等人(2021)提出了一项后续研究，重点关注不平衡流的数据级属性，如实例困难(边界和罕见实例)和子概念的存在。然而，这项研究已经完成对于有限数量的算法(5个分类器)，并且只关注两类问题。

Bernardo等人(2021)提出了针对不平衡数据流的方法的实验比较。他们使用不同水平的不平衡比和三种漂移速度扩展了Brzeziński等人(2021)的基准。然而，他们的研究分析了有限数量的算法(11个分类器)和三个真实世界的数据集。Cano和Krawczyk(2022)对30种专注于集成方法的算法进行了大量比较，但其中21种是通用集成，而不是不平衡的特定分类器。

这四个工作只解决二分类不平衡数据流。本文扩展了以往所有研究的基准评估，提出了新的基准场景，扩展了真实数据集的数量，并对两类和多类不平衡数据流进行了评估。我们还将比较扩展到24个分类器，其中19个是专门为不平衡数据流设计的。表1总结了这些作品在实验评价上的主要差异。这使我们得出结论，虽然这些工作是重要的第一步，但需要对从不平衡数据流中学习进行统一，全面和整体的研究，这些研究可以用作研究人员评估其新提出的算法的模板。

本文组织如下。第2节提供了数据流的背景知识。第3节讨论了不平衡数据的主要挑战。第4节介绍了不平衡流的具体困难。第5节描述了处理不平衡流的集成方法。第6节介绍了实验设置和方法。第7节给出并分析了我们的研究结果。第8节总结了经验教训。第9节为最终用户选择不平衡数据流的最佳算法提出了建议。第10节讨论了开放的挑战和未来的方向。最后，第11节给出了结论。

2 数据流

在本节中，我们将对数据流特征、学习方法和概念漂移特性的初步介绍。

2.1 数据流特征

数据流的主要特征可以概括如下(Gama, 2010;Krempl et al .， 2014;Bahri et al, 2021):

• 体积。流是潜在的无限数据集合，不断地淹没系统，因此它们不可能被存储，必须增量处理。体积也对计算资源施加了限制，这些资源比实际数据所需的大小要小得多。
• 速度。流数据源处于不断的运动中。新数据不断地产生，并且经常以快速爆发的方式产生，从而导致高速数据流。这些迫使学习系统实时工作，必须进行分析，并将其纳入学习系统，以模拟流的当前状态。
• 非定常性。数据流会随着时间的推移而变化，这被称为概念漂移。这种现象可能会影响特征分布、类边界，但也会导致类比例的变化，或新类的出现(或旧类的消失)。
• 真实性。来自流的数据可能是不确定的，并受到各种问题的影响，例如噪声、对抗性模式的注入或缺失值。由于成本和时间要求，访问完全标记的流通常是不可能的，这导致需要从弱标记的实例中学习。

可以将流$S$定义为序列$<s_1,s_2,s_3,\dots ,s_{\infty }>$。我们考虑一个有监督的场景$s_i=(X,y)$，其中$X=[x_1,x_2,\dots ,x_f]$，其中$f$为特征空间的维数，$y$为目标变量，目标变量在到达时可能可用，也可能不可用。流中的每个实例都是独立的，并且是从平稳的概率分布中随机抽取的。图1说明了从数据流中学习的工作流程和解决相关挑战的方法(Gama, 2012;Nguyen et al, 2015;Ditzler et al, 2015;ware et al，2019)。

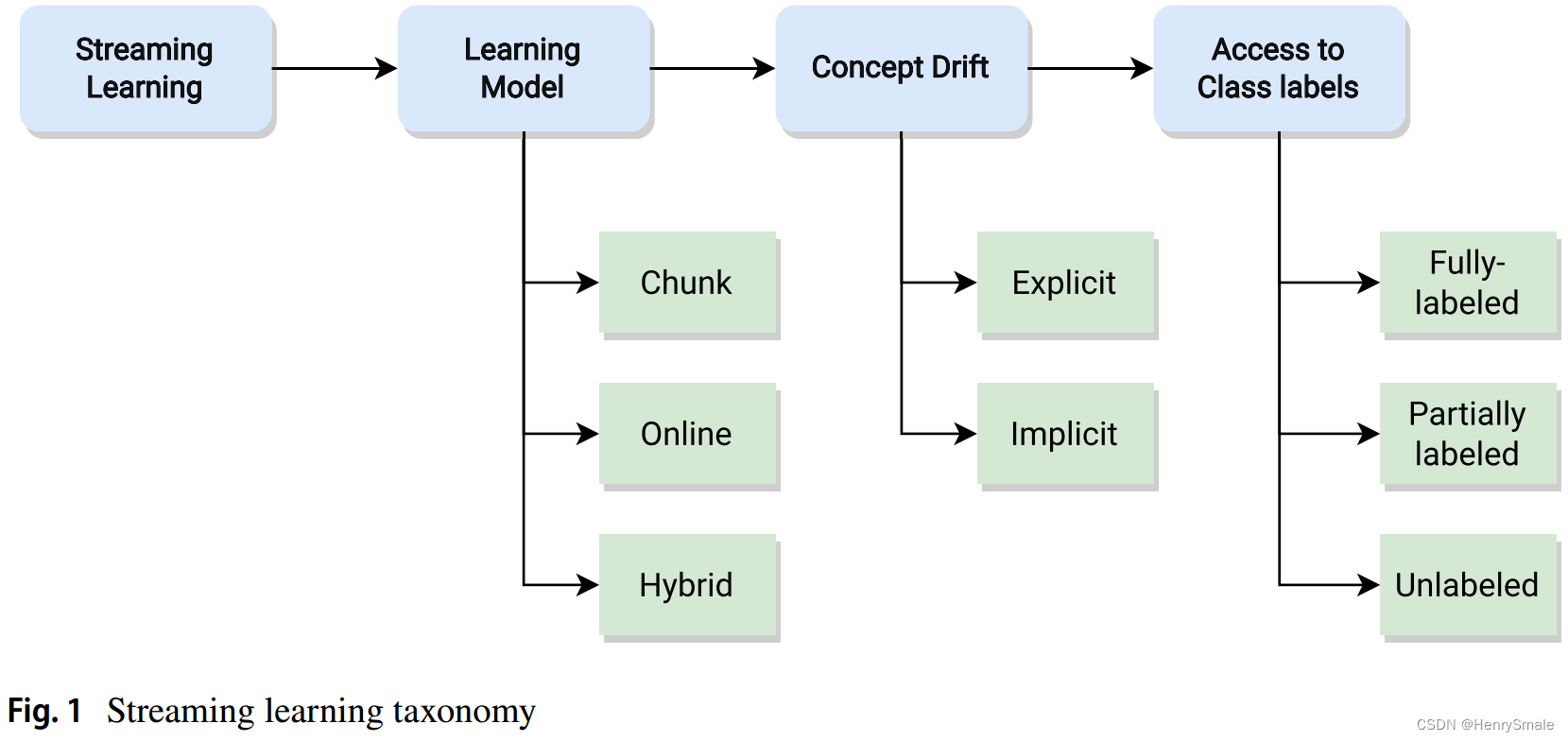
2.2 学习方法

由于数据流的体积和速度，算法需要能够对不断到达的信息进行增量处理。来自数据流的实例要么在线提供，要么以数据块(部分、块)的形式提供。

• 在线。算法将逐个处理每个单独的实例。这种方法的主要优点是响应时间短，对流中的变化适应性强。主要的缺点在于它们对流的当前状态的看法有限，因为单个实例可能不能很好地表示一个更大的概念，或者可能容易受到噪声的影响。
• 块。实例在称为数据块或块的窗口中处理。由于训练样本量较大，基于块的方法可以更好地估计当前概念。主要缺点是对某些设置更改的响应延迟，因为分类器的构造、评估或更新是在新块的所有实例可用时完成的。此外，在快速更改的情况下，块可能由来自多个概念的实例组成，这进一步损害了适应能力。
• 混合。混合方法可以结合前面的方法来解决它们的缺点。最流行的方法之一是使用在线学习，同时维护数据块以提取关于流的统计数据和有用的知识，以便进行额外的周期性分类器更新。

2.3 概念漂移

数据流受到一种称为概念漂移的现象的影响(Krawczyk等人，2017;Lu et al, 2018)。每个实例在时间$t$到达，由概率分布${\Phi }^t(X,y)$生成，其中$X$对应于特征向量，$y$对应于类标签。如果流中所有实例的概率分布相同，则数据是平稳的，即起源于相同的概念。另一方面，如果${\Phi }^t(X,y)$和${\Phi }^{t+C}(X,y)$生成了两个分别到达时间$t$和$t+C$的独立实例。如果${\Phi }^t\ne {\Phi }^{t+C}$，则发生了概念漂移。在分析和理解概念漂移时，需要考虑以下因素:

• 决策边界的影响。这里我们区分:(i)虚拟的;(ii)实际漂移类型。虚拟漂移可以定义为无条件概率分布$P(x)$的变化，这意味着它不影响学到的决策边界。这种漂移虽然不会对学习模型产生恶化的影响，但必须加以监测，因为它可能引发假警报，迫使人们进行不必要但代价高昂的适应。真正的概念漂移会影响决策边界，使其对当前概念毫无价值。检测它并适应新的分布对于保持预测性能至关重要。
• 变化的速度。在这里，我们可以区分三种类型的概念漂移(Webb et al, 2016):(i)增量;(ii)循序渐进;(iii)突发。增量漂移在新旧概念之间产生一系列的中间状态。这需要在新概念完全形成和相关时检测稳定时刻。在新旧实例之间逐渐漂移概念，随着时间的推移，新概念变得越来越频繁。突然的漂移会在新旧概念之间瞬间切换，导致底层学习算法的瞬间退化。
• 复发。流中的更改可以是唯一的，也可以是重复的。在后一种情况下，以前看到的概念可能会随着时间的推移而重新出现，使我们能够循环利用以前学过的知识。这就要求有一个模型存储库，可以用来更快地适应以前看到的变化。使用更宽松的假设，可以将递归扩展到与过去所见过的概念相似的外观。在这里，过去的知识可以作为漂移恢复的初始点。

有两种策略可以解决概念漂移: 显式和隐式(Lu等人，2018;Han等人，2022):

• 显式。在这里，漂移适应由称为漂移检测器的外部工具管理(Barros & Santos, 2018)。它们用于连续监控流属性(例如统计)或分类器性能(例如错误率)。漂移探测器在有即将发生漂移的迹象时发出警告信号，在概念漂移已经发生时发出警报信号。当检测到漂移时，分类器被替换为根据最近实例训练的新分类器。漂移检测器的缺陷是需要标记实例(半监督和无监督检测器也存在，但不太准确)和假警报来取代合格的分类器。
• 隐式。在这里，漂移适应是通过嵌入在分类器中的学习机制来管理的，假设它可以自我调整以适应来自最新概念的新实例，并逐渐忘记过时的信息(Ditzler等人，2015;da Costa等人，2018)。这需要建立适当的学习和遗忘率，使用自适应滑动窗口，或连续的超参数调整。

2.4 标签的使用

在数据流设置中获得类别标签涉及到大量的时间和成本要求。由于实例不断地大量到达，领域专家可能无法标记数据的重要部分，或者可能无法足够快地提供标签。对于可以免费获得标签的应用程序(例如天气预报)，必须考虑实例和标签到达之间的显著延迟。数据流可以分为三组关于类别标签的可用性:

• 完全标记。对于流中的每个实例$x$，标签$y$是已知的，可以用于训练。此场景假设不需要显式标签查询，并且是评估流学习算法的最常见场景。然而，对于许多实际应用程序来说，完全标记流的假设可能是不可行的。
• 部分标记。流中只有一小部分实例在到达时被标记。标记和未标记实例之间的比率可以随时间变化。这种情况需要主动学习来选择最有价值的实例进行标记(Žliobaitė等人，2013)，或者需要半监督机制来将知识从标记的实例扩展到未标记的实例(Bhowmick & Narvekar, 2022;Gomes et al, 2022)。
• 无标记。每一个实例到达时都没有标签，人们不能在要求时获得它，或者它将大大延迟到达。这迫使近似机制可以生成伪标签，寻找数据中的演变结构，或者使用延迟标签来近似未来的概念。

在这项工作中，只使用了完全标记的流，但评估的一些算法具有处理部分标记或未标记流的机制。

3 非平衡数据

在本节中，我们将简要讨论从不平衡数据中学习时面临的主要挑战。该领域近三十年的发展使我们能够更深入地了解在倾斜分布下是什么抑制了分类器训练过程的性能(Fernández等人，2018a)。

• 不平衡比率。不平衡数据集最明显和研究最充分的特性是它们的不平衡比率，即多数类和少数类之间的不平衡。通常认为，不平衡比率越高，分类器的难度越大。事实证明，大多数分类器训练过程是由0-1损失函数驱动的，这些损失函数假设每个实例的重要性是一致的。因此，多数类越占主导地位，分类器就越偏向于它。然而，最近的许多研究指出，比例失衡并不是学习困难的唯一来源(He & Ma, 2013)。只要类在训练集中被很好地分离和充分地表示，即使非常高的不平衡率也不会显著损害分类器。因此，我们必须研究实例级属性，以找到分类器偏差的其他来源。
• 样本量小。这种不平衡的比例通常伴随着这样一个事实，即少数类很少出现，收集足够数量的实例可能是昂贵的、耗时的，或者根本不可能的。这导致了小样本量的问题，其中少数类没有足够大的训练集来允许分类器正确捕获其特征(Wasikowski & Chen, 2010)。再加上失衡率高，会严重影响训练过程，导致泛化能力差和分类偏差。此外，小样本量不能保证训练集代表实际分布——这个问题被称为数据移位(Rabanser et al, 2019)。
• 类重叠。不平衡学习的另一个挑战来自类的拓扑结构，因为通常少数类和多数类都有很大的重叠。类重叠给标准机器学习问题带来了困难(Galar等人，2014)，而偏态分布的存在使其更具挑战性(Vuttipittayamongkol等人，2021)。重叠区域可以看作是分类器的不确定区域。在这种情况下，多数类将主导训练过程，导致决策边界忽略重叠区域的少数类。当处理多个相互重叠的类时，这个问题变得更加困难。
• 实例级的困难。类重叠问题指出了分析少数类实例的性质及其个体困难的重要性。少数类通常形成小的分离，产生子概念，进一步减少特定区域的少数类样本量(García et al .， 2015)。当看到对于每个实例的单个属性，可以分析它的邻域，以确定它对分类器的挑战性。一种流行的分类法根据其最近邻居的类别标签的同质程度将少数实例分为安全、边缘、罕见和异常值(Napierala & Stefanowski, 2016)。这些信息可以用来获得更有效的重采样方法或指导分类器训练过程。

4 非平衡数据流

类不平衡是当代机器学习中最重要的问题之一(Fernández等人，2018a;Wang et al, 2019)。它处理了每个类别中实例数量的不均衡，其中一些类别的代表性明显不足。由于大多数分类器是由0-1损失驱动的，它们倾向于更容易建模大多数类。代表性不足的少数类别通常是更重要的类别，因此需要改变数据集或学习过程，以创建不偏袒任何类的平衡决策边界。。

类不平衡是数据流挖掘领域的一个常见问题(Wu et al .， 2014;Aminian et al.， 2019)。这里的流可以有一个固定的不平衡比例，也可以随着时间的推移而变化(Komorniczak et al.， 2021)。此外，类失衡与概念漂移相结合，带来了新颖而独特的挑战(Brzeziński & Stefanowski, 2017;Sun et al, 2021)。类角色可能会转换(多数变成少数，反之亦然)，几个类可能会发生变化(新类出现或旧类消失)，或者实例级困难可能会出现(不断发展的类重叠或集群/子概念)(Krawczyk, 2016)。失衡比的变化可以是独立的，也可以与概念漂移有关，其中类定义($P(y\mid x)$)将随着时间的推移而变化(Wang & Minku, 2020)。因此，监视每个类的属性变化是不够的，因为还需要跟踪每个类到达新实例的频率。

在大多数现实生活场景中，流不是预先定义为平衡或不平衡的，它们可能只是暂时变得不平衡(Wang et al, 2018)。用户的兴趣随着时间的推移(新话题出现，旧话题失去相关性)(Wang等人，2014)，社交媒体分析(Liu等人，2020)或医疗数据流(al - shammari等人，2019)都是此类案例的例子。因此，无论底层类分布如何，稳健的数据流挖掘算法都应该显示出高的预测性能(Fernández等人，2018a)。大多数致力于不平衡数据流的算法在平衡问题上的表现不如规范对应的算法(Cano & Krawczyk, 2020)。另一方面，这些典型算法对高不平衡比的鲁棒性较低。目前很少有算法能够以令人满意的性能处理这两种情况(Cano & Krawczyk, 2020, 2022)。

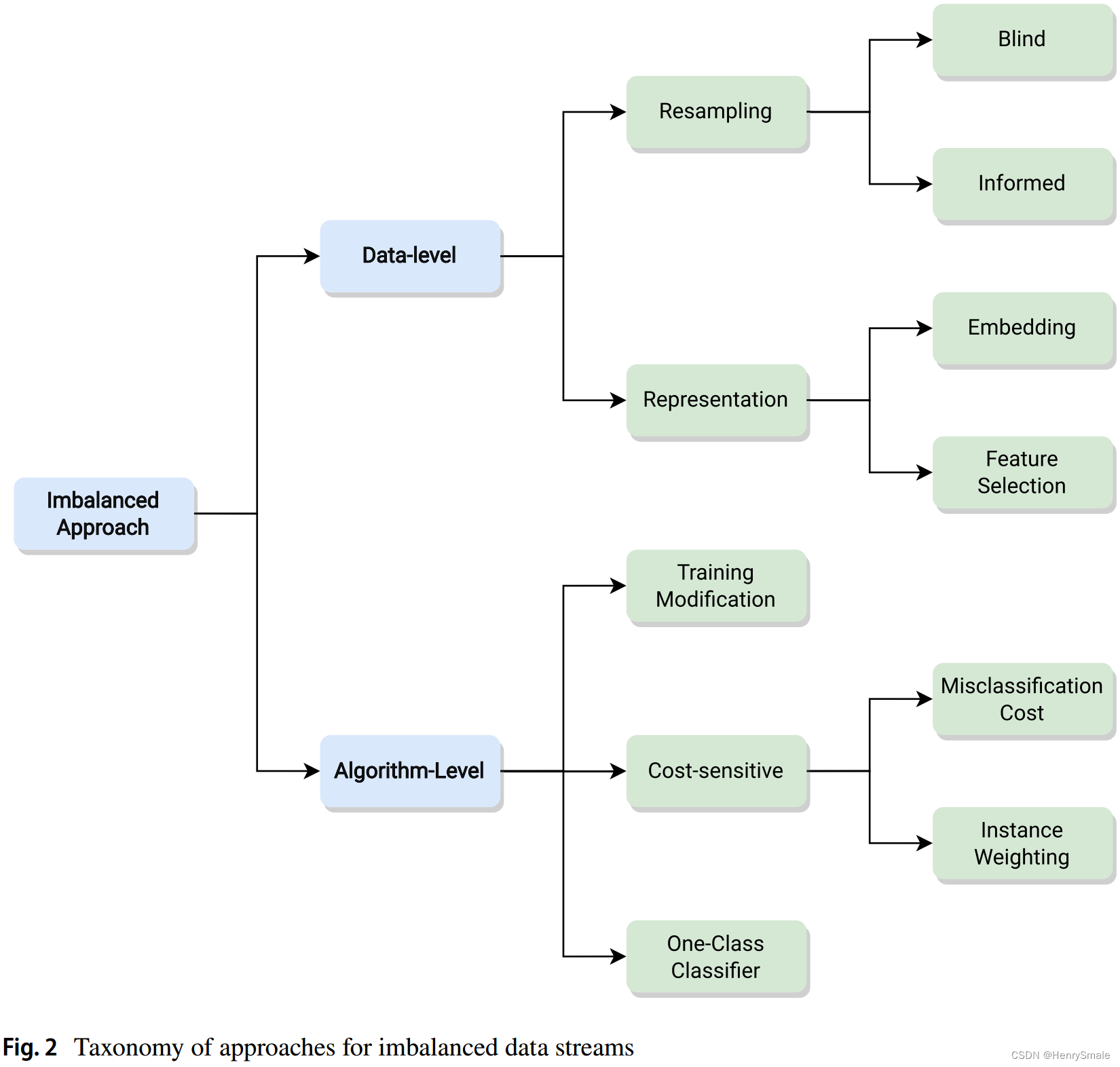
处理不平衡数据有两种主要方法:

• 数据级方法。这些方法侧重于改变底层数据集以使其平衡(例如，通过过采样或欠采样)，因此是分类不可知的方法。他们专注于重新采样或学习更稳健的表示。
• 算法级方法。这些方法的重点是修改训练方法，使分类器对偏态分布具有鲁棒性。它们专注于特定的学习模型，通常更专业，但不如数据级的方法灵活，算法级别的修改侧重于识别受类不平衡、代价敏感学习或单类分类影响的机制。

图2给出了一个分类(He & Garcia, 2009;Branco et al.， 2016;2016年,杰哈卡胡奇;Fernández等人，2018a)解决类失衡问题的方法。具体细节将在以下小节中讨论。

4.1 数据级方法

4.2 算法级方法