题目:
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4] 输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1] 输出:0
提示:
1 <= target <= 1091 <= nums.length <= 1051 <= nums[i] <= 105
算法原理:
暴力解法基础上的优化:
暴力解法是依次固定左边界,从左边界开始依次作为右边界加入sum,计算和,当和>=target且小于上一次的结果就更新结果
暴力解法存在很多不必要且重复的计算:
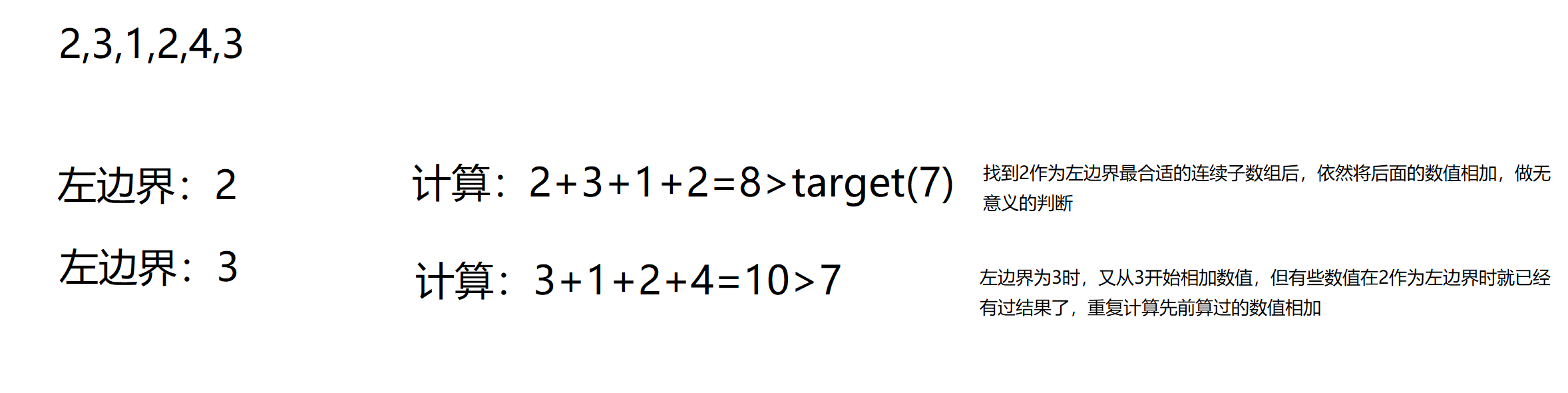
滑动窗口(优解):
滑动窗口其实就是同向指针,left指针和right指针都不会回退
初始化:left=0 (左边界)right=0(待进入窗口的数值)
1 进窗口:让right指针指向的数值加入sum中
2 判断:若是sum>=target(已是当前left指向数值作为左边界找到的满足条件的最短连续子数组,right指针没必要往后面走,再让sum加入一些数值,因为只要再加入数值,一定是比target大的,但是又增加了长度,所以没必要) 且比上一次的结果要小则更新结果
3 出窗口:left指向的数值作为左边界已有自己的最优结果,sum-=nums[left++]
重复步骤2的判断,因为出了原先的nums[left] ,新数值作为左边界时也可能已经满足条件 sum>=target(right指针依然是原nums[left]做左边界时,能够找到的最优右边界),如right指向的数值加入后使得sum远远大于target,那么出了一个元素,可能会使得剩下的元素依然>=target
4 结束条件:right>=n

代码实现:
class Solution
{
public:int minSubArrayLen(int target, vector<int>& nums){int sum = 0;int len = INT_MAX;//注意不能初始化为0,因为是找最小int left = 0;int right = 0;int n = nums.size(); while(right<n){sum+=nums[right];//进窗口while(sum>=target)//判断{len = min(len,right-left+1);//更新结果sum-=nums[left++];//出窗口}right++;}return len==INT_MAX?0:len;}
};






![[Linux]进程程序替换](https://img-blog.csdnimg.cn/img_convert/1c00060c235a79e036660c24ca8b853d.png)