🔆 文章首发于我的个人博客：欢迎大佬们来逛逛

线性优化

使用 Yalmip 求解线性规划最优值：

m i n { − x 1 − 2 x 2 + 3 x 3 } x 1 + x 2 ⩾ 3 x 2 + x 3 ⩾ 3 x 1 + x 3 = 4 0 ≤ x 1 , x 2 , x 3 ≤ 2 \begin{gathered}min\{-x_1-2x_2+3x_3\} \\x_1+x_2\geqslant3 \\x_2+x_3\geqslant3 \\x_1+x_3=4 \\0\leq x_1,x_2,x_3\leq2 \end{gathered} min{−x1​−2x2​+3x3​}x1​+x2​⩾3x2​+x3​⩾3x1​+x3​=40≤x1​,x2​,x3​≤2​

• 使用 sdpvar 来构建实数解，如果要求解整数类型，则使用 intvar；如果是01类型，使用binvar
• 构建目标函数
• 构建约定与LB,UB上下限，其中 ≥ ≤ == 等约束直接照抄即可
• optimize求解最优值。
• 打印结果…

clc;clear;
%
p = sdpvar(3,1);
%% 构建目标函数
Objective = -p(1)-2*p(2)+3*p(3);
%% 构建约束
Constraints = [0<=p<=2,(p(1)+p(2)>=3),(p(2)+p(3)>=3),(p(1)+p(3)==4)];
%% 求解最优值
optimize(Constraints,Objective);
%%
% 三个变量的解
P=double(p);
% 目标优化值
Obj=double(Objective);
objstr=['目标函数最优值：',num2str(Obj)];
disp(objstr)
for i=1:length(P)xstr=['x',num2str(i),'的值为：',num2str(P(i))];disp(xstr)
end

---

整数规划

在 optimize 函数中添加如下参数来实现 01整数规划。

• options = sdpsettings(‘solver’, ‘bnb’, ‘bnb.solver’, ‘fmincon’);
• options = sdpsettings(‘solver’,‘bmibnb’, ‘bmibnb.uppersolver’, ‘fmincon’); 全局最优，但是速度慢

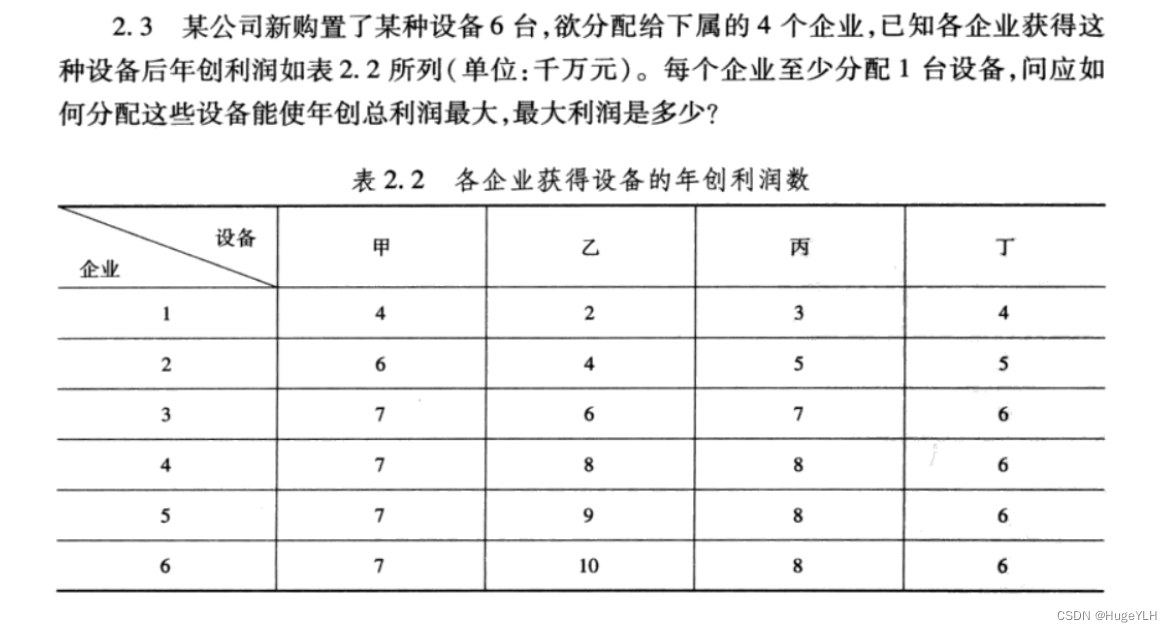
案例（1）

clc;clear;p = binvar(6,4); % 01整数规划
%%
c = [4,2,3,4;6,4,5,5;7,6,7,6;7,8,8,6;7,9,8,6;7,10,8,6;
];
%%
f = -sum(sum(p.*c));
%% 构建约束：注意二维矩阵的构建方法
cons = [];
for j = 1:size(c,2)cons = [cons,(sum(p(:,j))>=1)];
end
%%
for i = 1:size(c,1)cons = [cons,(sum(p(i,:))==1)];
end
%% 整数规划
% options = sdpsettings('solver', 'bnb', 'bnb.solver', 'fmincon');
options = sdpsettings('solver','bmibnb', 'bmibnb.uppersolver', 'fmincon');
%%
optimize(cons,f,options);%%
% 三个变量的解
P=double(p);
% 目标优化值
Obj=double(-f);
objstr=['目标函数最优值：',num2str(Obj)];
disp(objstr)
disp(P);

---

案例（2）

clc;clear;p = intvar(7,1);
%%
f = sum(p);
%%
% 必须写上限制范围
cons = [0<=p,(p(1)+2*p(2)+p(7)>=100),(3*p(3)+2*p(4)+p(5)+p(7)>=100),(4*p(1)+p(2)+2*p(4)+4*p(5)+6*p(6)+p(7)>=100)];
%% 整数规划
% options = sdpsettings('solver', 'bnb', 'bnb.solver', 'fmincon');
% options = sdpsettings('solver','bmibnb', 'bmibnb.uppersolver', 'fmincon');
%%
optimize(cons,f);%%
% 三个变量的解
P=double(p);
% 目标优化值
Obj=double(f);
objstr=['目标函数最优值：',num2str(Obj)];
disp(objstr)
for i=1:length(P)xstr=['x',num2str(i),'的值为：',num2str(P(i))];disp(xstr)
end

---

案例（3）

clc;clear;p = binvar(5,8);
%%
c = [ 30 25 18 32 27 19 22 26;29 31 19 18 21 20 30 19;28 29 30 19 19 22 23 26;29 30 19 24 25 19 18 21;21 20 18 17 16 14 16 18];%% 
f = sum(sum(c.*p));%%
constraints = [];
for j = 1:size(c,2)constraints = [constraints,(sum(p(:,j))<=1)];
endfor i = 1:size(c,1)constraints = [constraints,(sum(p(i,:))==1)];
end
%%
options = sdpsettings('solver','bmibnb', 'bmibnb.uppersolver', 'fmincon');%% 
optimize(constraints,f,options);%%
% 三个变量的解
P=double(p);
% 目标优化值
Obj=double(f);
objstr=['目标函数最优值：',num2str(Obj)];
disp(objstr)
disp(P);

---

非线性规划

$$\begin{gathered} \max f(x)=2x_1+3x_1^2+3x_2+x_2^2+x_3, \\ \text{s. t.}\{\begin{array}{l}{x}_1+2x_1^2+x_2+2x_2^2+x_3⩽10,\\ x_1+x_1^2+x_2+x_2^2-x_3⩽50,\\ 2x_1+x_1^2+2x_2+x_3⩽40,\\ x_1^2+x_3=2,\\ x_1+2x_2⩾1,\\ x_1⩾0,x_2,x_3\text{ 不约束}.\end{array} \end{gathered}$$

clc;clear;p = sdpvar(3,1);
%% 
f = -2*p(1)-3*p(1)^2-3*p(2)-p(2)^2-p(3);%%
Cons = [(p(1)>=0),(p(1)+2*p(1)^2+p(2)+2*p(2)^2+p(3)<=10),(p(1)+p(1)^2+p(2)+p(2)^2-p(3)<=50),(2*p(1)+p(1)^2+2*p(2)+p(3)<=40),(p(1)^2+p(3)==2),(p(1)+2*p(2)>=1)];
%%
% options = sdpsettings('solver','bmibnb', 'bmibnb.uppersolver', 'fmincon');
%% 
optimize(Cons,f);
%%
% 三个变量的解
P=double(p);
% 目标优化值
Obj=double(-f);
objstr=['目标函数最优值：',num2str(Obj)];
disp(objstr)
disp(P);