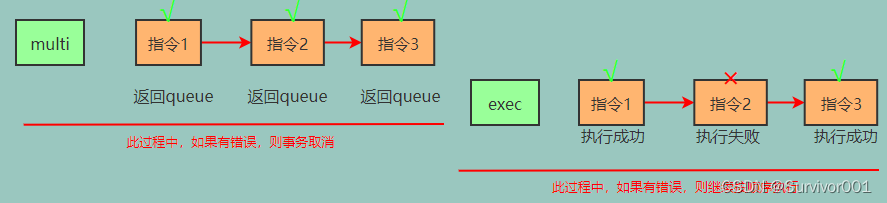
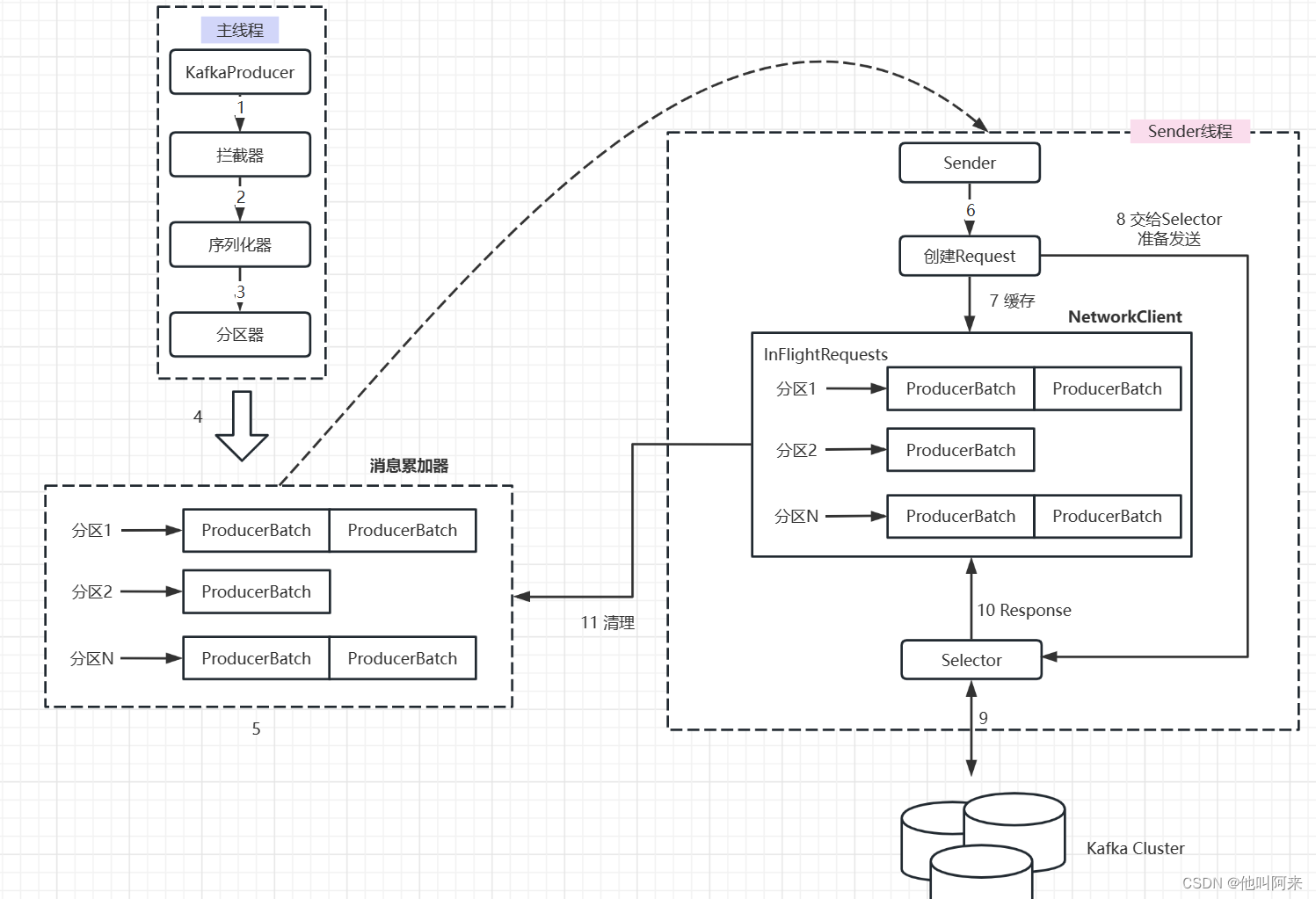
一、Real-Time Global Illumination(in 3D cont.)
上篇只介绍了RSM,这里我们还会简要介绍另外两种在3D空间中做全局光照的方法,分别是LPV和VXGI。
1.Light Propagation Volumes (LPV)

首先我们知道Radiance在传播过程中是不会被改变的,这点我们都知道。
其次LPV将空间划分成了许多小格子,也叫Voxel(体素)。而这些Voxel就是用来传播间接光照的Radiance的。我们很容易知道直接光照,参考RSM的思路。然后通过知道哪些格子是次级光源来计算每个格子接受到的Radiance,这就是LPV的基本思路。

第一步,找到直接光打到的表面,这步和RSM无区别,当然,有多少光源就需要多少RSM。其次,也不是必须把所有被直接光打到的表面都当作次级光源,可以用采样的方式,我们之前都说过。这样我们就得到了一系列次级的虚拟的光源。
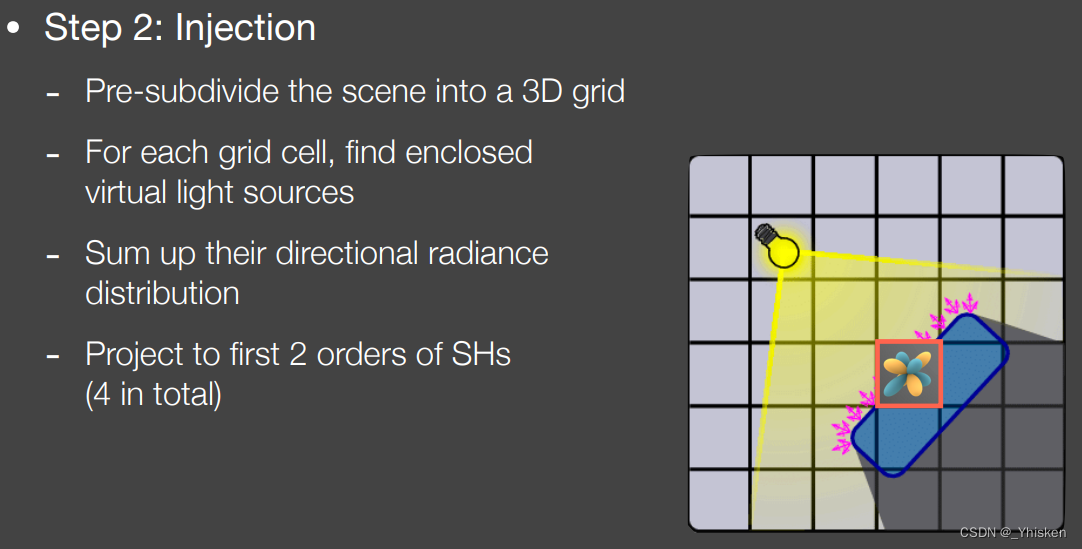
得到了次级光源我们就可以把它们注入到相应的格子里,变成格子的属性,这样我们就知道每个格子往各个方向的Radiance初始值都是多少,而这是个空间的分布,自然我们就可以用前面提到的SH压缩它。(工业界常用2阶)

第三步就是传播了,那么Radiance如何传播呢?很简单,次级光源所在的格子里有向四周传播的Radiance,而Radiance又是按直线传播的。自然,一个格子6个面,穿过它上表面格子的Radiance自然就会被它上面的格子接受到,其它面的Radiance同理,同样其它的格子里的Radiance分布也可以用SH所表示(这里和RSM一样,我们不考虑传播过程中的Visibilty)。如此不断迭代,直到最后整个网格稳定下来。(差不多迭代4,5次)
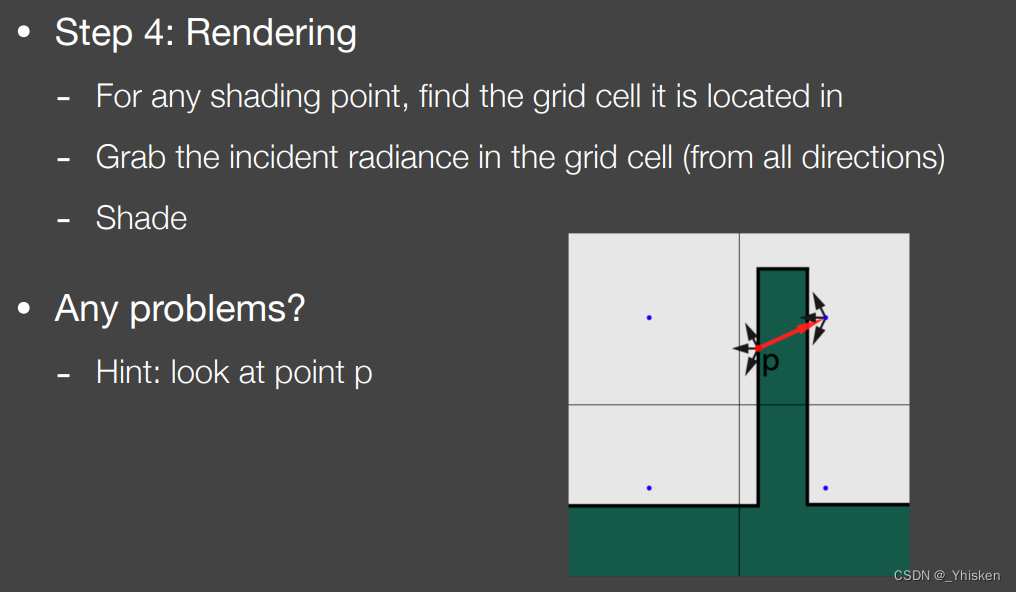
第四步自然就是渲染了,对于任意的着色点,我们都知道它们在哪个格子里,我们还知道它们的Incident Radiance,就可以渲染了。
当然,这其中会有问题,如上图所示。场景中的几何比划分的格子小的时候就会很容易发生这种情况。如图p点为直接光照照亮的点,它是次级光源,显然它右边有一面墙,它绝对不可能照到墙右边的部分,但由于LPV的Radiance是用格子存储的,我们会认为这个格子里都是相同的Radiance。于是墙右边被照亮了,这显然是错误的。但如果把格子划分的非常非常细,虽然可以解决这种问题,但随之而来的自然是存储量问题,以及Radiance传播的计算量问题。不过当然,我们可以自适应划分一些格子的分辨率,如工业界常用的Cascade方法。
2.Voxel Global Illumination(VXGI)

VXGI和RSM相同,是一个双Pass的算法(LPV相当于4Pass)。VXGI把场景彻底离散化成了体素(参考MineCraft/乐高积木)。并且还会把这些格子组成一个树形结构,有不同的层级。
所以与RSM不同的是,RSM的次级光源是每一个小片,而VXGI的次级光源是体素。
其次VXGI的第二个Pass与RSM和LPV都不同,它的第二个Pass从Camera出发,打出Camera Ray,而假设当Camera Ray打到某个Glossy材质对应的片元所在位置,自然就会变成一个锥形的分布,然后这个锥形与之前得到的次级光源所在体素相交,就可以知道这个着色点得到的贡献是多少了。
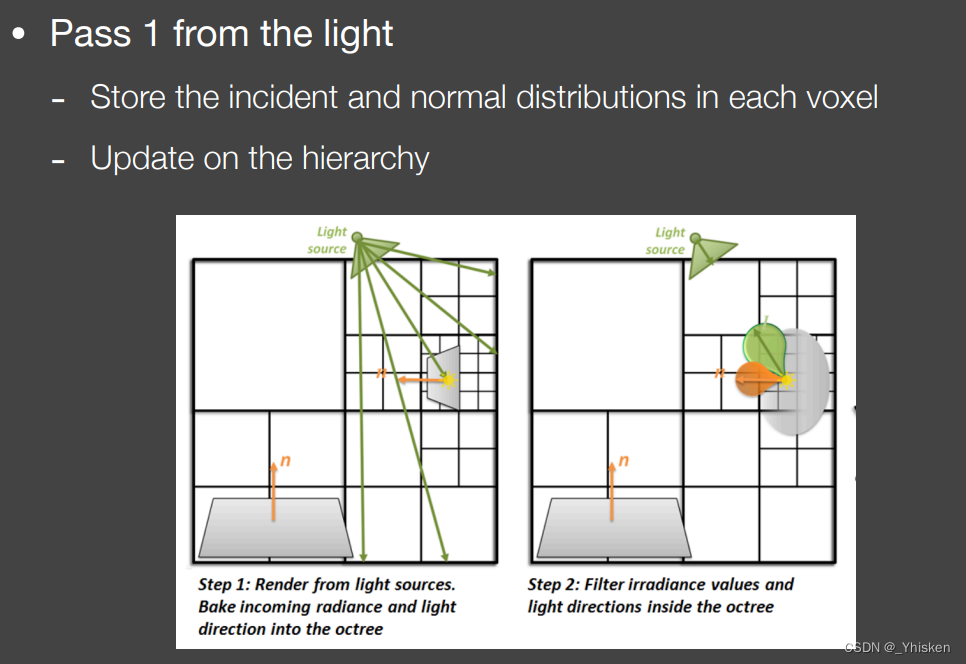
Pass1,计算直接光照,和RSM和LPV类似,但这里我们可以不再认为所有反射物都是Diffuse的了 ,这里我们会在Voxel体素中的表面上记录一个入射光的分布(如上图绿色所示),还会记录该表面的用来反射的法线分布(如上图橙色所示),并且我们还知道这个表面是Diffuse还是Glossy的自然就可以计算出它的出射分布,这比我们直接假设默认Diffuse的方法会准确一些。由此我们还可以在小格子记录分布后整合到更高的层级,形成一个层次结构。
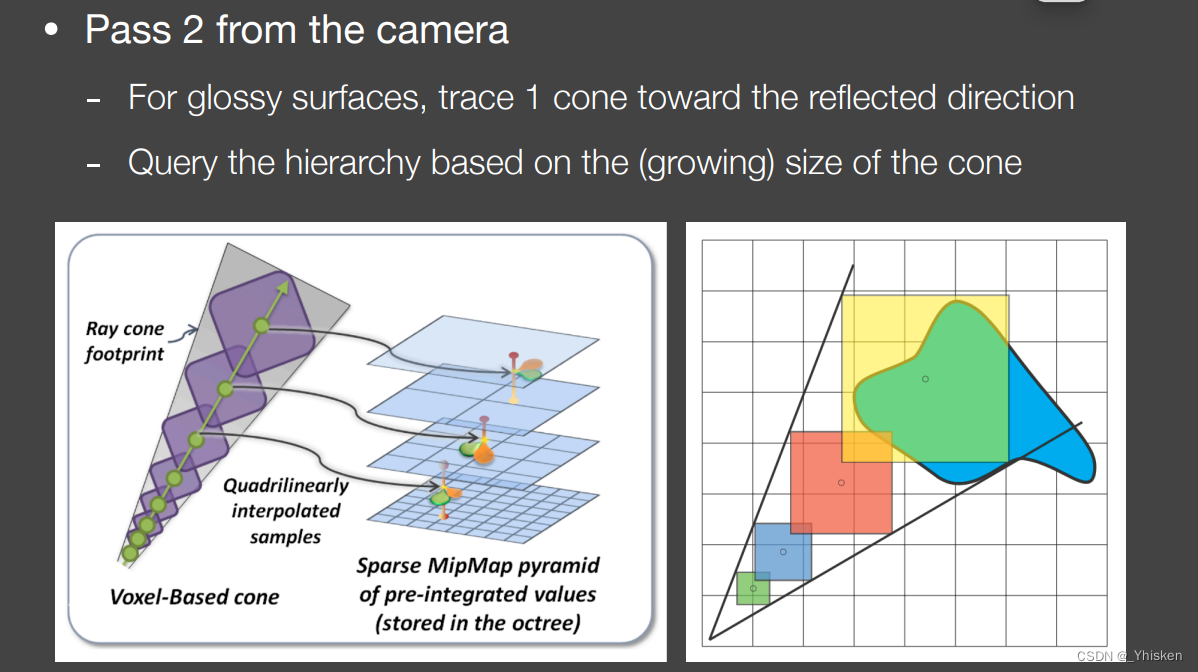
Pass2从Camera出发发射的Camera Ray(假如是Glossy)经过着色点后会被反射成圆锥,我们叫它Ray cone,它会随着传播的距离增大而变大。之后计算它与哪些体素相交,再把贡献加在一起就可以了。不过既然Ray cone范围会越来越大,我们可以直接在之前体素的层次结构中找对应的层级体素记录的分布信息即可。这就是VXGI的基本思路。
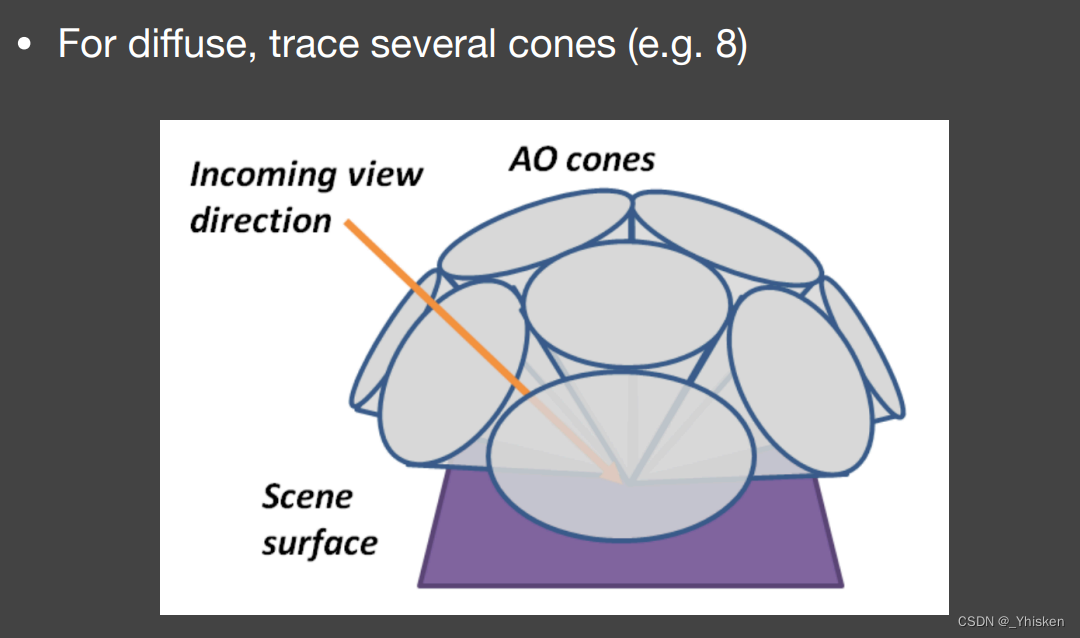
而对于Diffuse物体,VXGI的发明者们的做法是用差不多8个圆锥来覆盖半球以此近似Diffuse的情况。
当然对于VXGI,它也有一些问题。首先我们要对整个场景进行体素化,这是需要预处理的,而如果是动态物体,那每一帧都要实时体素化,显然会非常慢。以及对于Diffuse的情况,圆锥增多,查询次数自然也会增多。
二、Real-Time Global Illumination (screen space)

屏幕空间限定了我们获取信息的范围,也就是说我们得到的信息仅仅能从屏幕上能看到的东西上获取,相当于一个后处理。而对于做GI之前,那我们能得到的信息自然也就是直接光照了。
Screen Space Ambient Occlusion (SSAO)—屏幕空间环境遮蔽

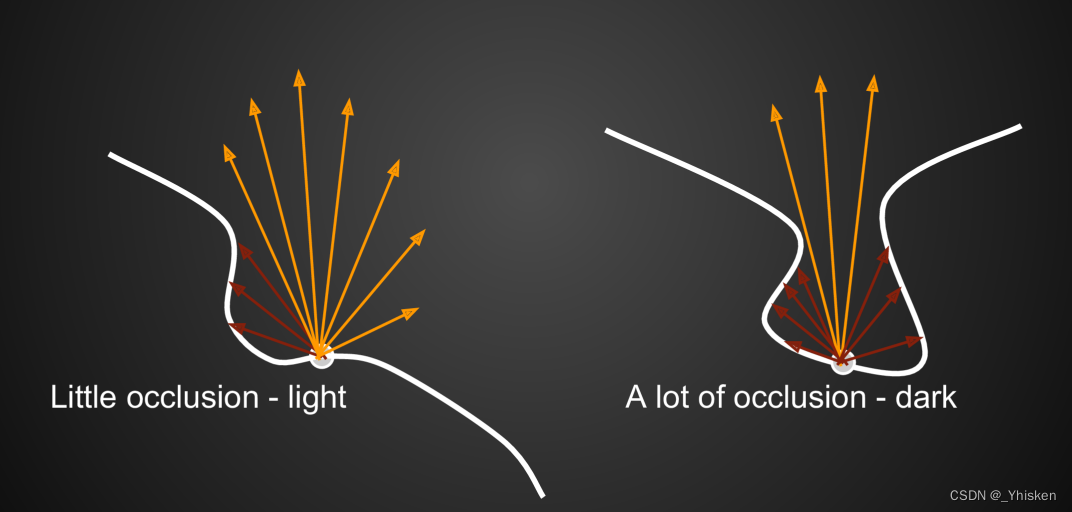
环境遮蔽(Ambient Occlusion) —简称AO,简单的说就是物体缝隙间光线难以到达的地方会有些发暗的现象,如上图的对比图。
那么屏幕空间的环境遮蔽是什么呢?其实就是全局光照的一种近似,因为AO本身就是由全局光照造成的。并且我们只能通过在屏幕中获取的看到的可见信息来做,如法线,深度等。
(1)Idea

那么SSAO是怎么做的呢?首先,我们不知道着色点的间接光照是什么,但是我们可以假设它们的四面八方的间接光照是一个常数,也就是我们之前说的Blinn-Phong模型那样。

但是,相比于Blinn-Phong模型好的地方在于,虽然我们仍然假设四面八方的间接光照是一个常数,但不见得所有着色点都能接收到它,也就是我们考虑了Visibility,这样就会有几何的遮挡关系。
(2) Theory

从数学上来理解SSAO,自然就要回到咱们的渲染方程上来,同时回顾一下我们经常用的上图所示的约等式,它可以把Visibility项拆出去。

可以看到,拆出Visibilty项后就是上图蓝框里所示的部分,下面的积分就是π。那整个其实就是一个加权平均了,我们设为kA,它的值自然就是0~1。其次橙色框的部分实际上就是我们事先给定的数,BRDF是Diffuse的,所以是常数,间接光我们一开始也给定的是常数,所以就固定下来了。
(3)Deep understanding*(可忽略)

一个更深的理解,我们上一步已经说了拆出的Visibility项其实就是f(x)的加权平均。那我们更进一步,SSAO这个公式完全就可以理解成,在g(x)的覆盖范围内,f(x)的平均值是多少。而我们之前说过这个约等式要想准确符合的条件,这里由于g(x)我们上面说过是常数,那就肯定是smooth的,所以这个约等式是成立且准确的。

还有一个问题,我们拆分之后,按照拆分的约等式,为什么本来是对dω积分,现在变成了对cosθdω积分呢?如何解释这个问题呢?

这里我们引入另外一个概念,Projected solid angle—投影立体角,我们之前说立体角实际上对应了单位球面上一个面积,那自然,投影立体角是投影后的立体角,对应的就是单位球下单位元的一块面积。对投影立体角积分得到的自然就算单位圆的面积,也就是π*1*1,也就是π。所以我们上面写成对cosθdω积分实际上是对投影立体角积分,这也就解释了我们为什么能如此拆分。
(4)Compute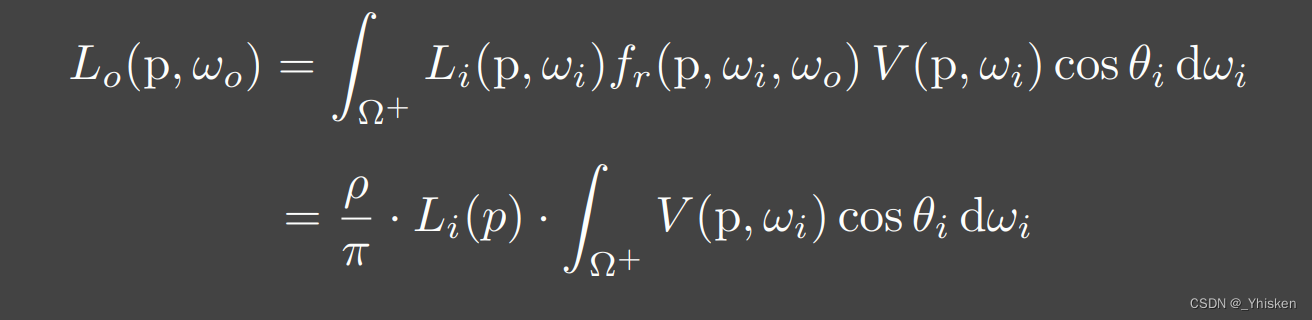
上面的Deep understanding只是为了更深层次的理解SSAO,实际上单从渲染方程上来看很简单,如上图,因为我们已经认定了BRDF和Li都是常数,那就都提出去就好了,积分中只剩Visibility项。
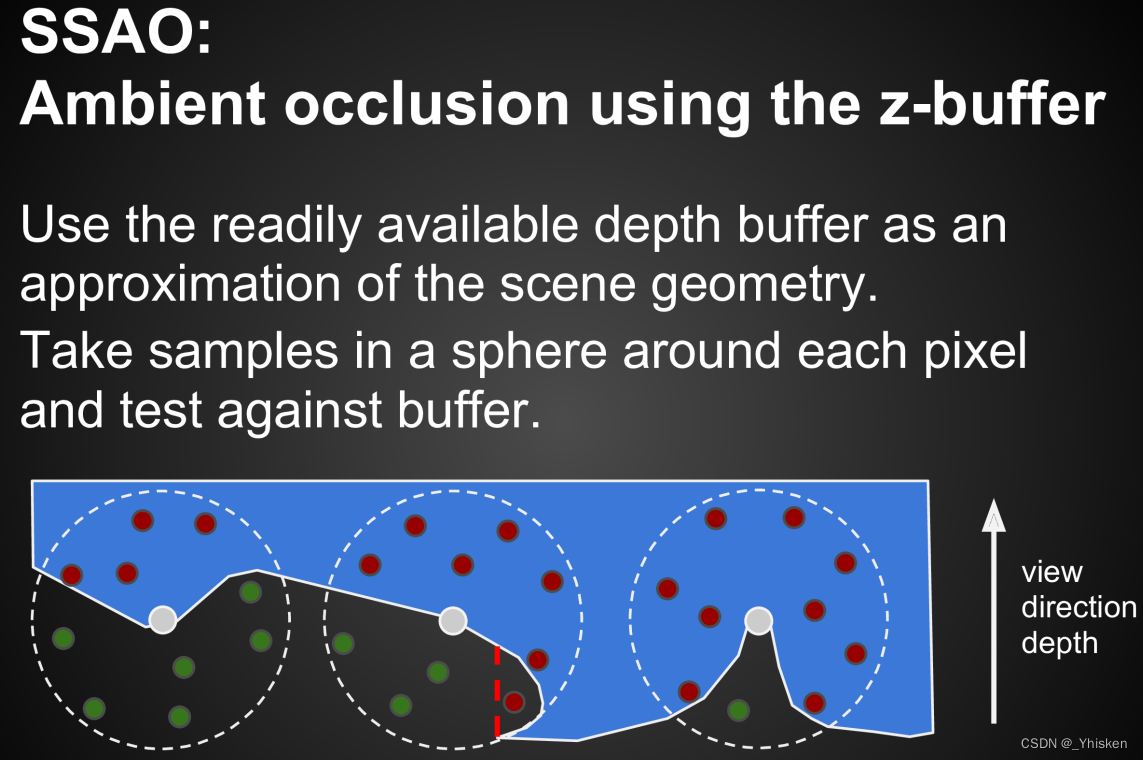
那现在我们怎么计算这个值呢?SSAO提供了一个方法,那就是在任何一个着色点的整个球的体积内采样,然后判断这些采样点能不能被着色点看到。那怎么判断采样点在物体内外呢?这要通过深度图来判断,深度图是我们在屏幕上看到的最浅深度,一定程度上描述了场景的几何,这时如果我们把采样点投影到Camera上,那么采样点的深度Zs和Z-Buffer中记录的最浅深度Z做比较,就可以知道采样点是不是在物体内了,若Zs>Z,那就说明采样点在物体内,反之则在物体外。
当然有一种意外情况,如上图中间的情况,几何体有一个拐角,但是由于我们的Z-Buffer记录的是最浅深度,所以无法区分这种情况。

还有个问题,我们判断整球没有意义,因为法线另外半球着色点是肯定看不到的,所以判断整球会造成一个很大的浪费,我们事实上只需要判断法线方向半球就足够了,但是在SSAO被发明的那个年代还无法从屏幕上获取法线,所以人们采取了另外一种方法:只有看不到的采样点(上图所示红点)占比超过50%的时候才考虑AO问题,然后只计算另一半的红点占比就可以了。因为产生AO一定程度上就是红点过半导致的。
当然,即使是这样,因为没有法线而导致的无法cos进行加权还是会导致结果没那么准确,只是一个近似。
(5)False occlusions

SSAO也会产生一些False occlusion的问题,如上图,近处的石凳对远处的地板居然产生了AO,这显然是不对的,两个物体离的这么远,石凳是不可能对地板产生遮蔽的。究其原因,是因为在地板球上的一些采样点投影到屏幕上之后和石凳的最浅深度比较的时候大于石凳的最浅深度,于是错误的认为是红点,所以产生了遮蔽。
如果减小采样半径,一定程度上可以解决问题,但是自然可能也会丢失一些True occlusion。也就是原本该遮挡的地方没有遮挡,一切都是取舍问题。
(6)Other
• 采样问题
SSAO仍然做了采样,那么自然就有我们前面提到的所有采样方法共有的问题,采样点数量的取舍,越多的采样点自然意味着更好的质量,但会牺牲速度。
人们通常在使用SSAO时会使用较少的采样点生成一个Noisy的AO,然后再做一遍模糊,这样就能得到相对较好的结果,因为实际玩游戏的时候很少有人会盯着AO看。
• HBAO—Horizon Based Ambient Occlusion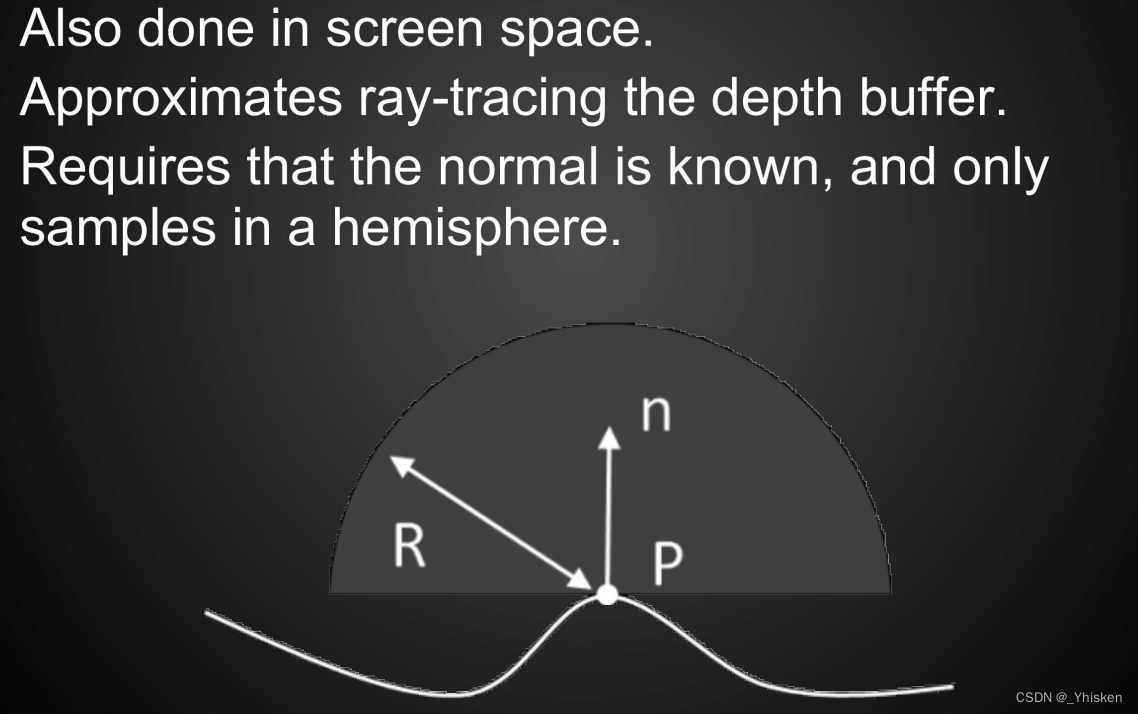
之前我们说,因为SSAO在发明的时候人们在屏幕上很难获取到法线,但是现在可以,于是就有了HBAO。有了法线,我们自然就知道要在哪半球采样,然后算之前的红点占比。
其次,有法线,我们还可以对各个方向进行加权了,就可以得到相对来说更准确的值。其次,HBAO不会有SSAO的False occlusion问题,因为它真的考虑了一定范围距离的问题。
参考
GAMES202_Lecture_08 (ucsb.edu)
Lecture8 Real-time GLobal Illumination (screen space)_哔哩哔哩_bilibili