本文涉及的概念分布包括:
-
随机变量(Random Variable)
-
密度函数(Density Functions)
-
伯努利分布(Bernoulli Distribution)
-
二项式分布(Binomial Distribution)
-
均匀分布(Uniform Distribution)
-
泊松分布(Poisson Distribution)
-
正态分布(Normal Distribution)
-
长尾分布(Long-Tailed Distribution)
-
学生 t 检验分布(Student’s t-test Distribution)
-
对数正态分布(Lognormal Distribution)
-
指数分布(Exponential Distribution)
-
威布尔分布(Weibull Distribution)
-
伽马分布(Gamma Distribution)
-
卡方分布(Chi-square Distribution)
-
中心极限定理(Central Limit Theorem)
01
随机变量
离散随机变量
随机实验的所有可能结果都是随机变量。一个随机变量集合用 表示。
如果实验可能的结果是可数的,那么它被称为离散随机变量。例如,如果你抛硬币 10 次,你能得到的正面数可以用一个数字表示。或者篮子里有多少苹果仍然是可数的。
连续随机变量
这些是不能以离散方式表示的值。例如,一个人可能有 1.7 米高,1米 80 厘米,1.6666666…米高等等。
02
密度函数
我们使用密度函数来描述随机变量 的概率分布。
PMF:概率质量函数
返回离散随机变量 等于 的值的概率。所有值的总和等于 1。PMF 只能用于离散变量。
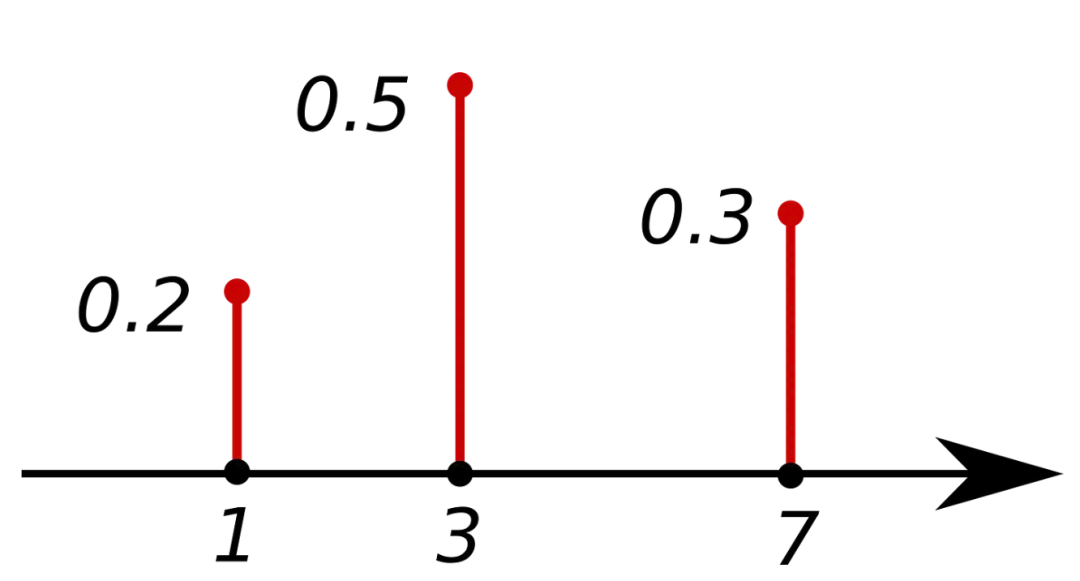
PMF。来源:https://en.wikipedia.org/wiki/Probability_mass_function
PDF:概率密度函数
它类似于连续变量的 PMF 版本。返回连续随机变量 X 在某个范围内的概率。
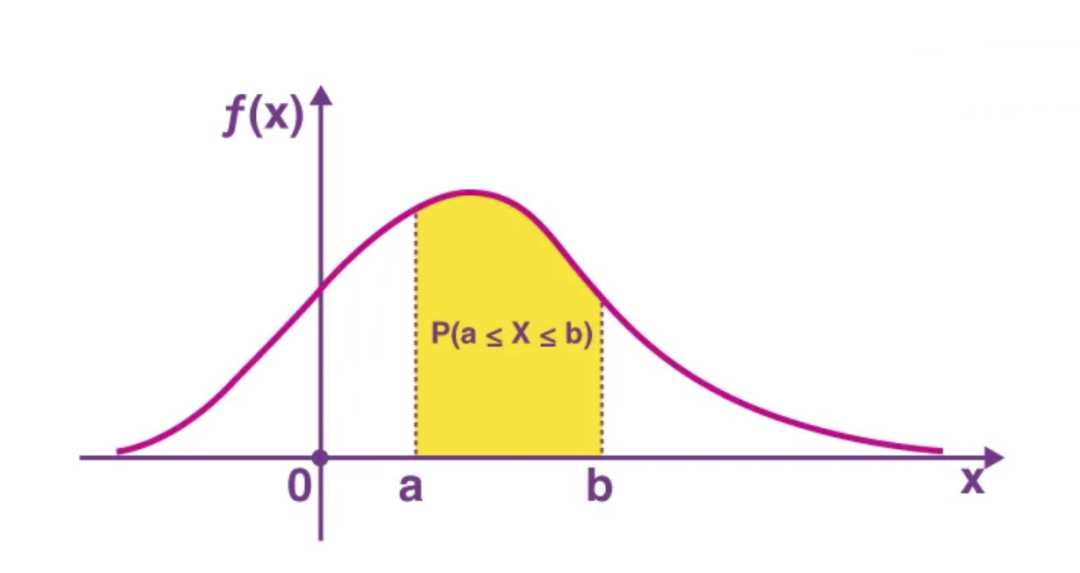
PDF。来源:https://byjus.com/maths/probability-density-function/
CDF:累积分布函数
返回随机变量 X 取小于或等于 x 的值的概率。
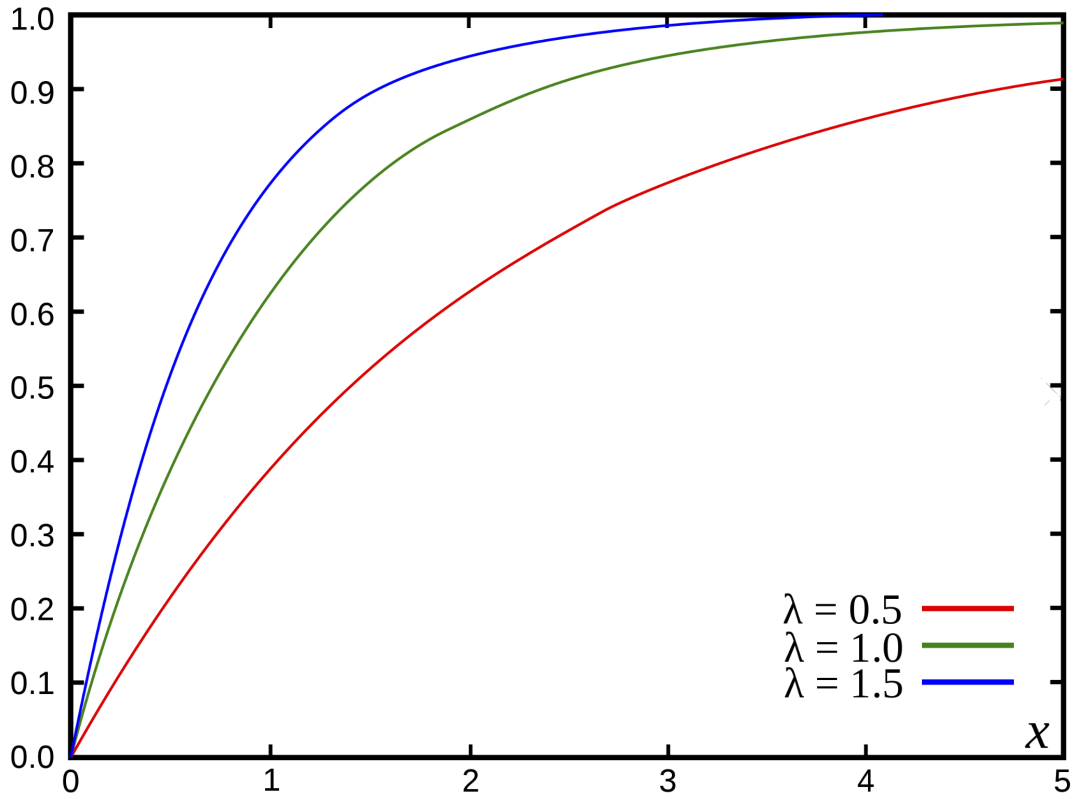
CDF(指数分布的累积分布函数)。来源:https://en.wikipedia.org/wiki/Cumulative_distribution_function
03
离散分布
伯努利分布
我们只有一个试验(只有一个观察结果)和两个可能的结果。例如,抛硬币。
我们有一个真的(1)的结果和一个假的(0)的结果。假设我们接受正面为真(我们可以选择正面为真或成功)。那么,如果正面朝上的概率是 ,相反情况的概率就是 。
import seaborn as sns
from scipy.stats import bernoulli
# 单一观察值
# 生成数据 (1000 points, possible outs: 1 or 0, probability: 50% for each)
data = bernoulli.rvs(size=1000,p=0.5)
# 绘制图形
ax = sns.distplot(data\_bern,kde=False,hist\_kws={"linewidth": 10,'alpha':1})
ax.set(xlabel='Bernouli', ylabel='freq')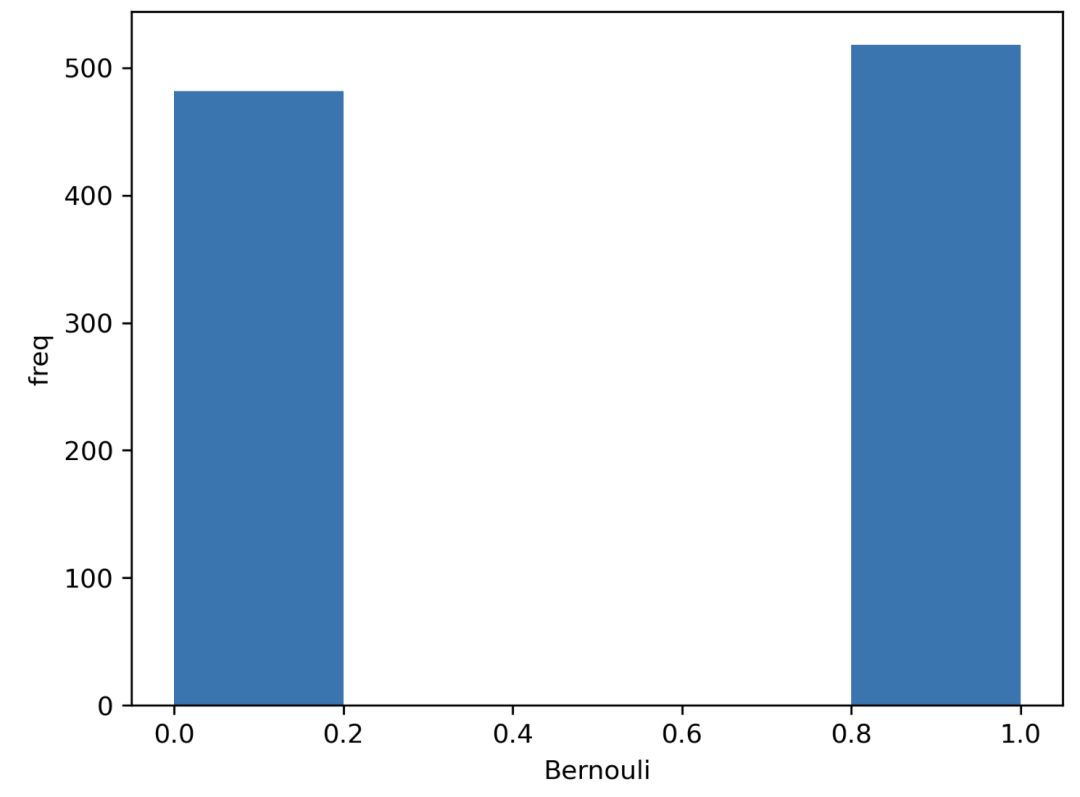
二项式分布
伯努利分布是针对单个观测结果的。多个伯努利观测结果会产生二项式分布。例如,连续抛掷硬币。
试验是相互独立的。一个尝试的结果不会影响下一个。
二项式分布可以表示为 , 。 是试验次数, 是成功的概率。
让我们进行一个实验,我们连续抛掷一枚公平的硬币 20 次。
import matplotlib.pyplot as plt
from scipy.stats import binom
n = 20
# 实验次数
p = 0.5
# 成功的概率
r = list(range(n + 1))
# the number of success
# pmf值
pmf\_list = \[binom.pmf(r\_i, n, p) for r\_i in r \]
# 绘图
plt.bar(r, pmf\_list)plt.show()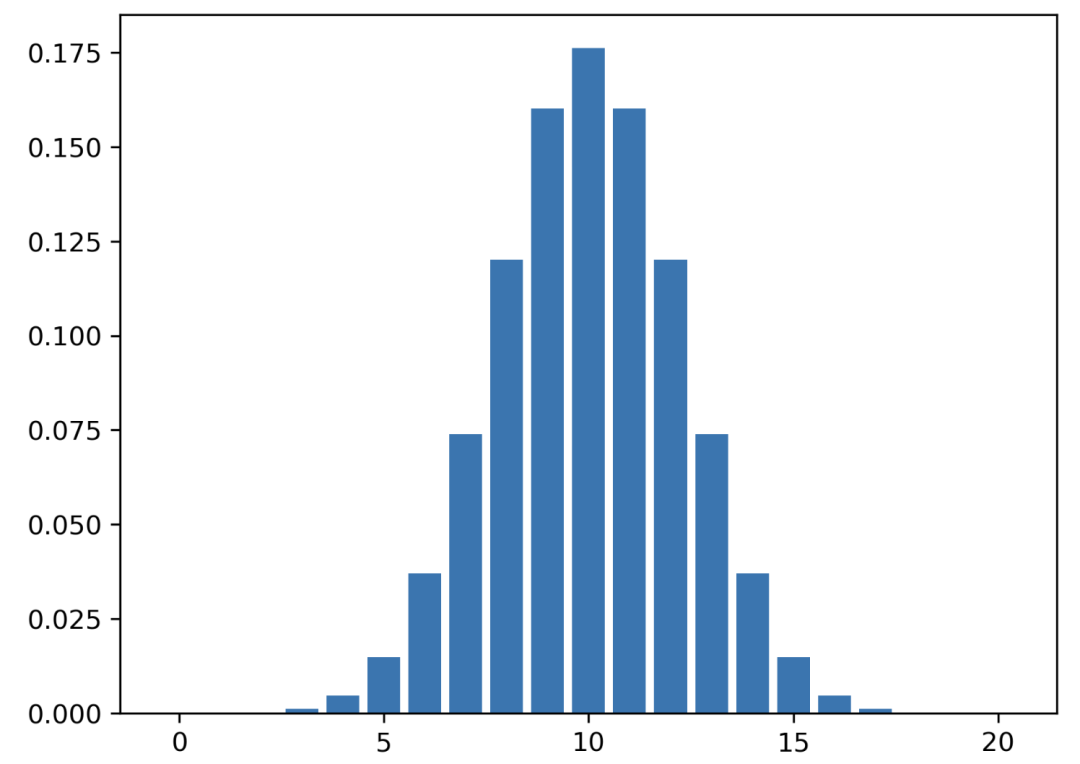
它看起来像正态分布,但请记住这些值是离散的。
现在这次,你有一枚欺诈硬币。你知道这个硬币正面向上的概率是 0.7。因此,p = 0.7。
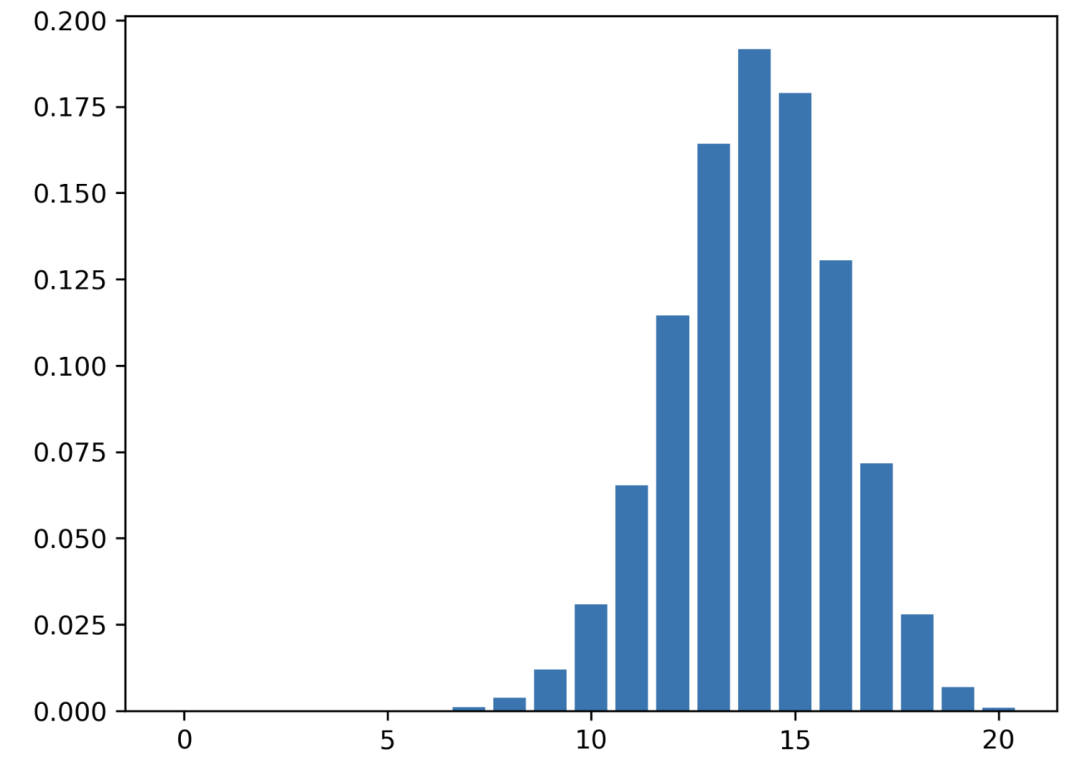
带有偏差硬币的二项式分布
- 该分布显示出成功结果数量增加的概率增加。
- 成功的概率 : 实验次数 : 失败的概率
均匀分布
所有结果成功的概率相同。掷骰子,1 到 6。
掷 6 次。
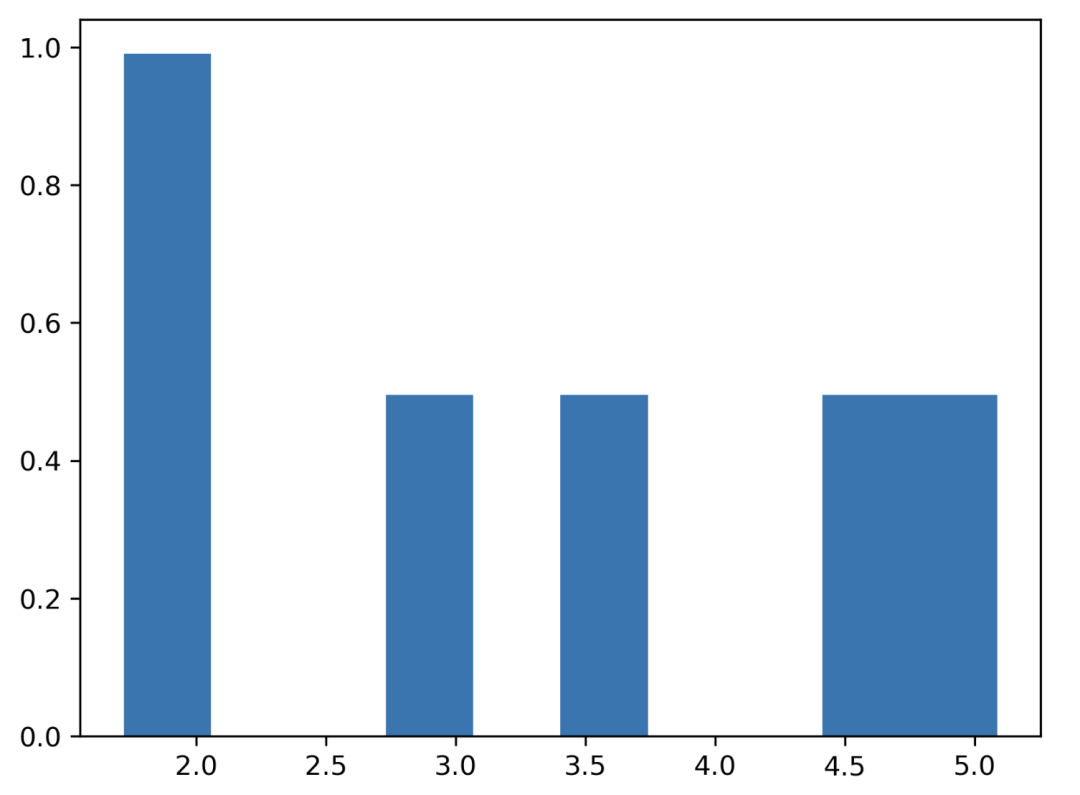
data = np.random.uniform(1, 6, 6000)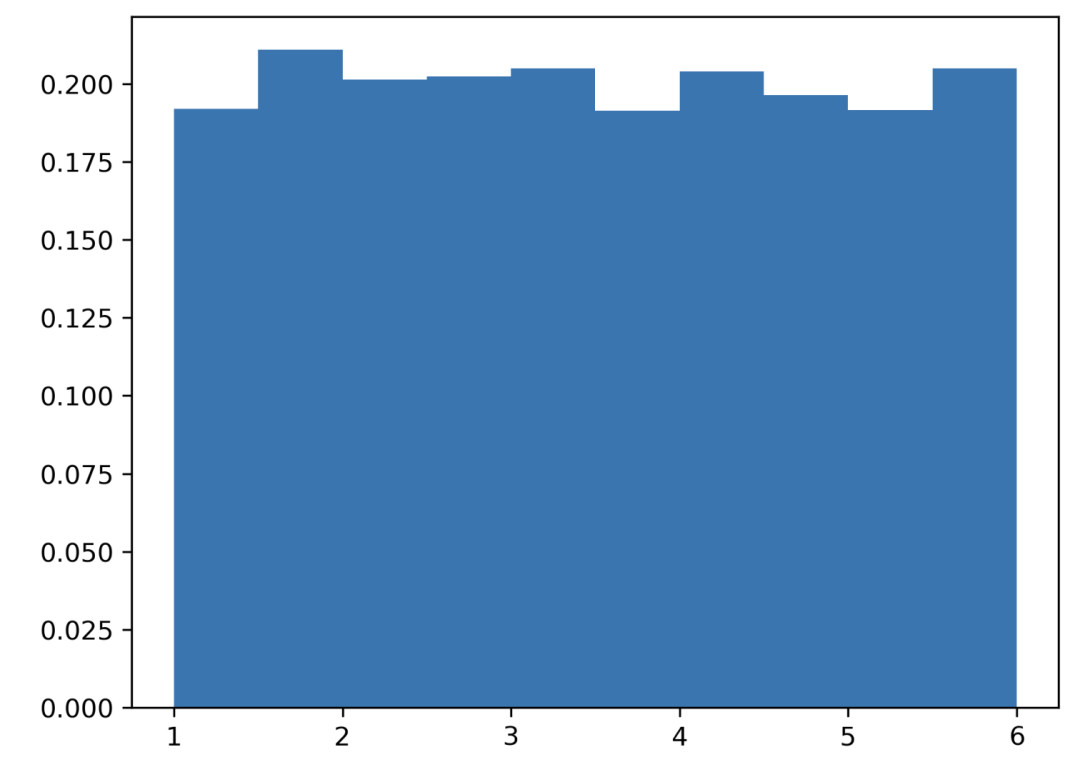
掷 6000 次。
Poisson 分布
它是与事件在给定时间间隔内发生频率相关的分布。
, 是在指定时间间隔内预期发生的事件次数。它是在该时间间隔内发生的事件的已知平均值。 是事件在指定时间间隔内发生的次数。如果事件遵循泊松分布,则:
在泊松分布中,事件彼此独立。事件可以发生任意次数。两个事件不能同时发生。
如每 60 分钟接到 4 个电话。这意味着 60 分钟内通话的平均次数为 4。让我们绘制在 60 分钟内接到 0 到 10 个电话的概率。
import matplotlib.pyplot as plt
from scipy.stats
import poisson
r = range(0,11)
# 呼叫次数
lambda\_val = 4
# 均值
# 概率值
data = poisson.pmf(r, lambda\_val)
# 绘图
fig, ax = plt.subplots(1, 1, figsize=(8, 6))
ax.plot(r, data, 'bo', ms=8, label='poisson')
plt.ylabel("Probability", fontsize="12")
plt.xlabel("# Calls", fontsize="12")
plt.title("Poisson Distribution", fontsize="16")
ax.vlines(r, 0, data, colors='r', lw=5, alpha=0.5)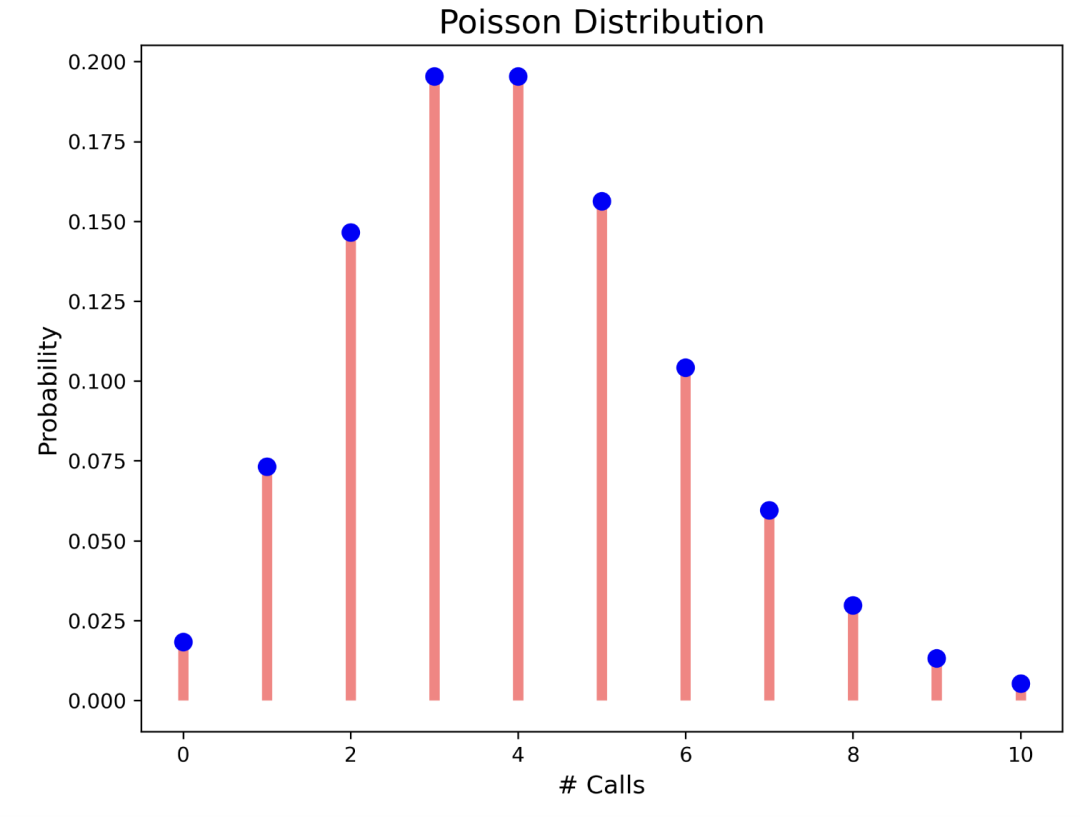
04
连续分布
正态分布
最著名和最常见的分布(也称为高斯分布),是一种钟形曲线。它可以通过均值和标准差定义。正态分布的期望值是均值。
曲线对称。均值、中位数和众数相等。曲线下总面积为 1。
大约 68%的值落在一个标准差范围内。~95% 落在两个标准差范围内,~98.7% 落在三个标准差范围内。
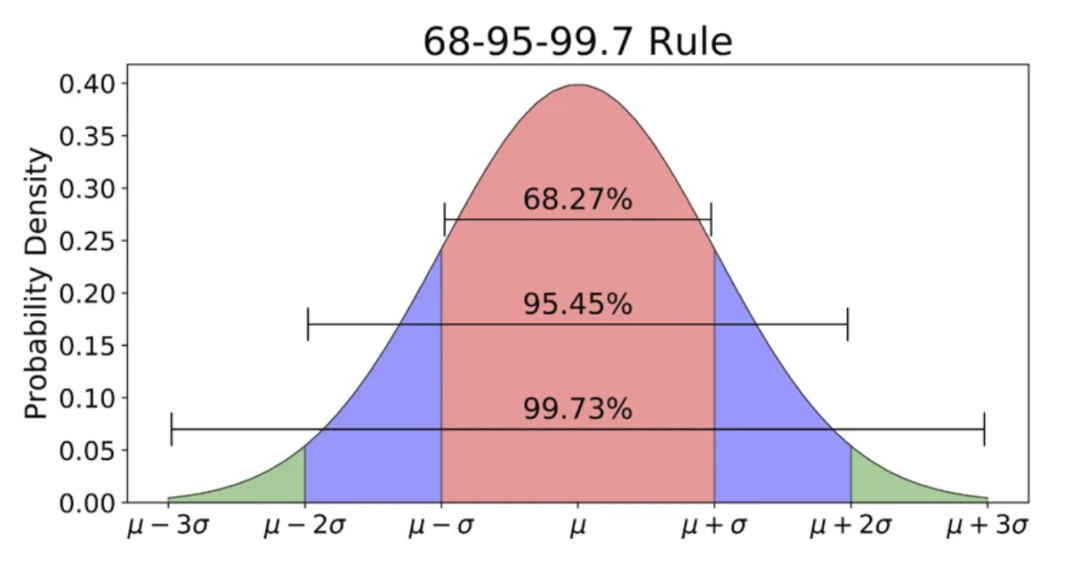
import scipy
mean = 0
standard\_deviation = 5
x\_values = np. arange(\-30, 30, 0.1)
y\_values = scipy.stats.norm(mean, standard\_deviation)
plt.plot(x\_values, y\_values. pdf(x\_values))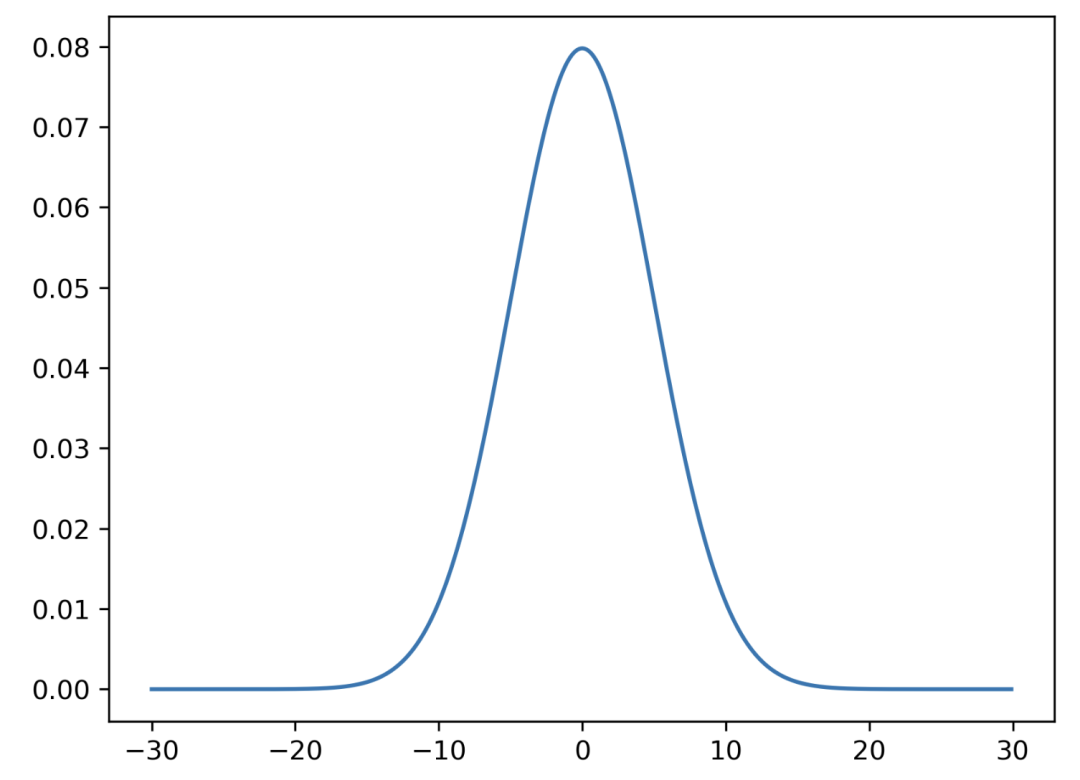
正态分布的概率密度函数为:
是均值, 是常数, 是标准差。
QQ 图
我们可以使用 QQ 图来直观地检查样本与正态分布的接近程度。
计算每个数据点的 z 分数并对其进行排序,然后在 y 轴上表示它们。X 轴表示值的排名的分位数。
这个图上的点越接近对角线,分布就越接近正态分布。
import numpy as np
import statsmodels.api as sm
points = np.random.normal(0, 1, 1000)
fig = sm.qqplot(points, line ='45')
plt.show()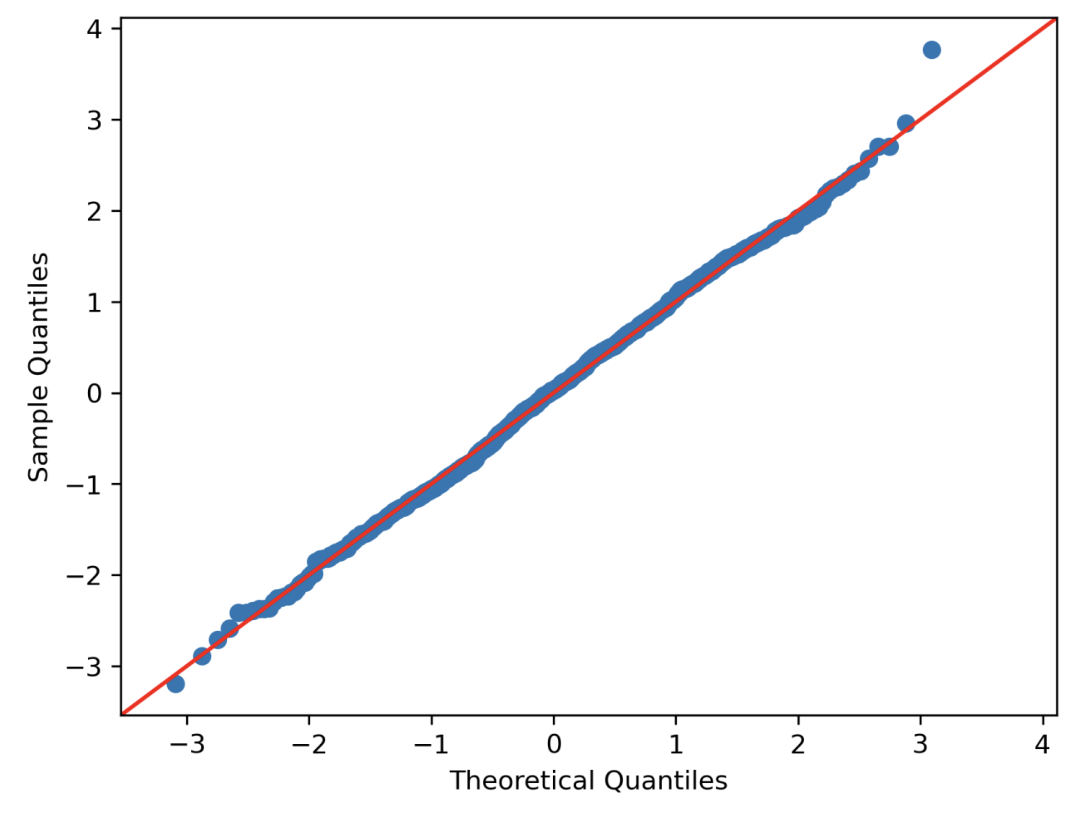
长尾分布
尾巴是分布的长而窄的部分,离群值就位于其中。当一侧尾巴不同于另一侧时,就称为偏斜。下图是长尾分布的 QQ 图。
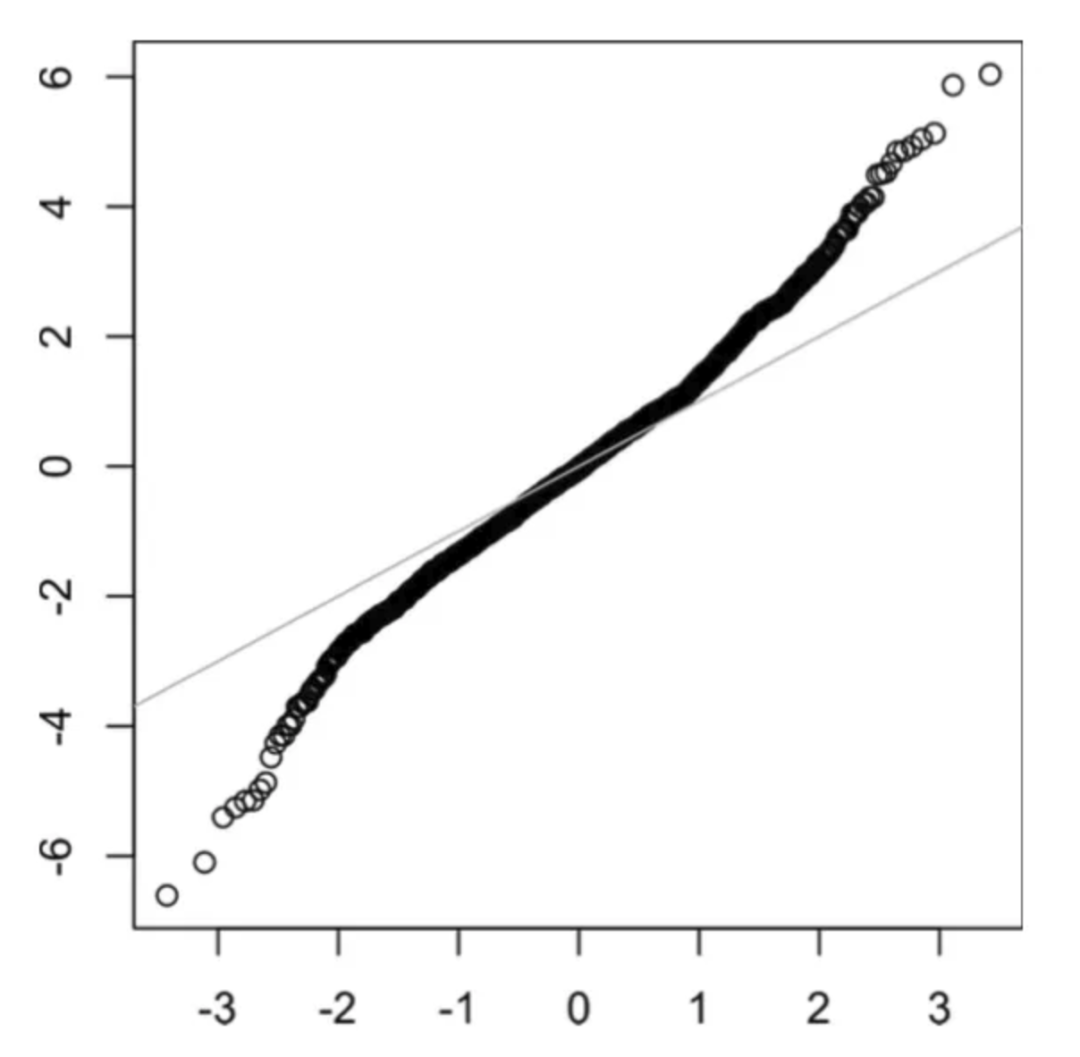
import matplotlib.pyplot as plt
from scipy.stats import skewnorm
def generate_skew_data(n: int, max_val: int, skewness: int):
Skewnorm function
random = skewnorm.rvs(a = skewness,loc=max_val, size=n)
plt.hist(random,30,density=True, color = ‘red’, alpha=0.1)
plt.show()
generate_skew_data(1000, 100, -5) # negative (-5)-> 左偏分布
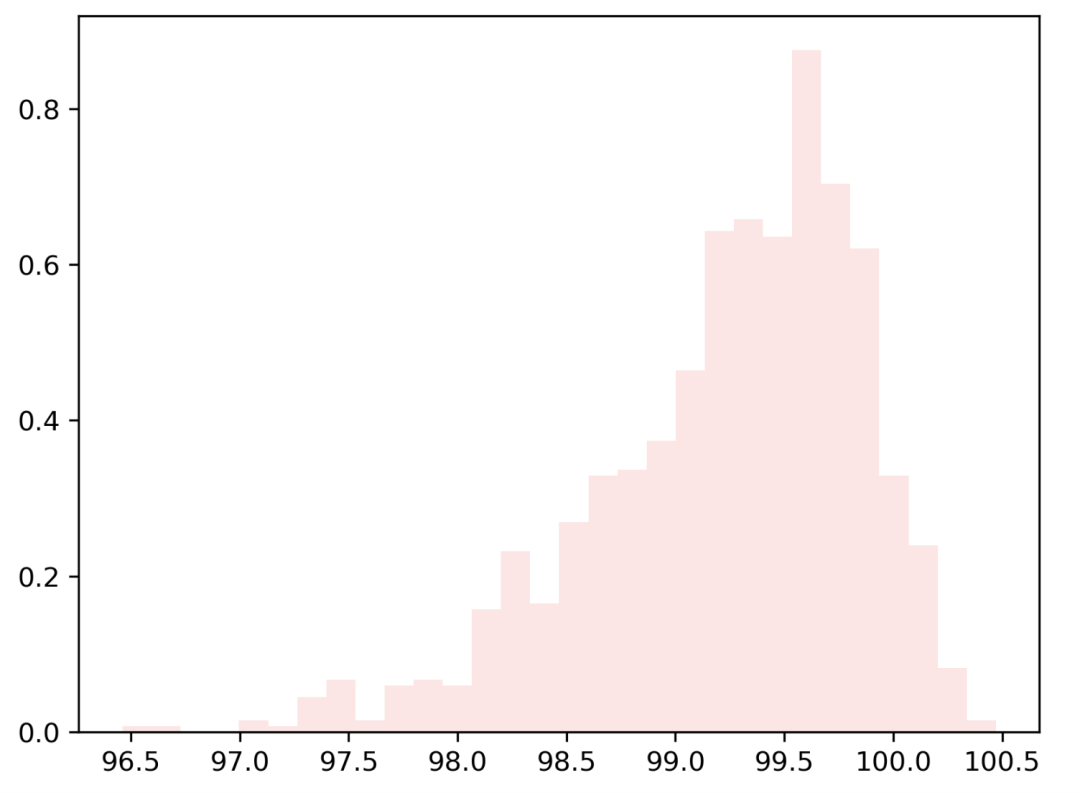
generate_skew_data(1000, 100, 5) # positive (5)-> 右偏分布

学生 t 检验分布
正态但有尾(更厚、更长)。
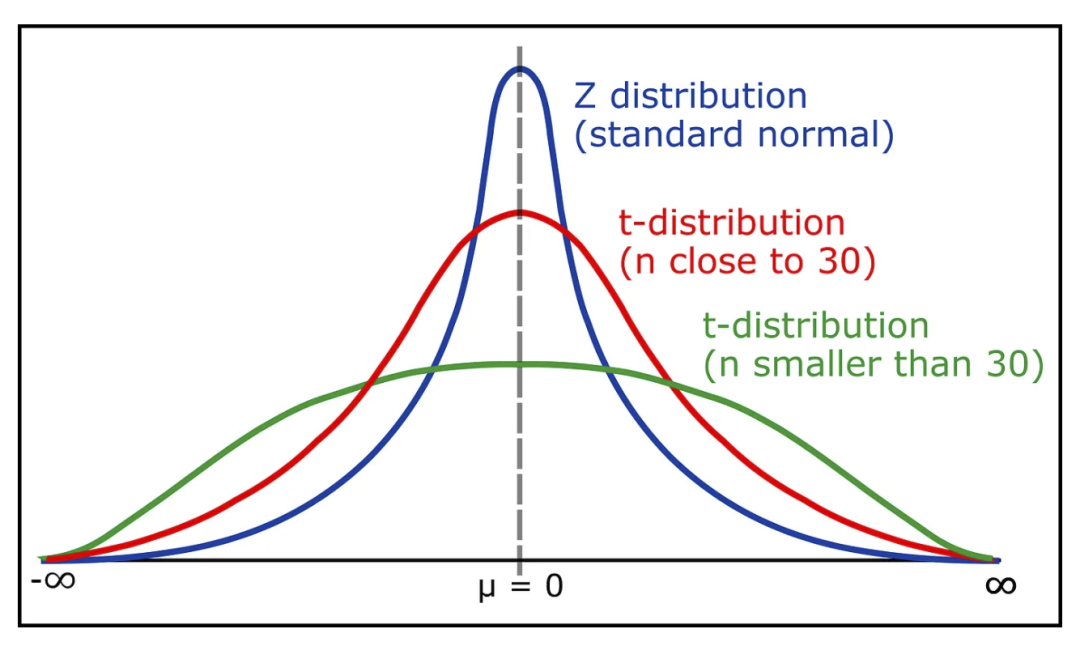
t 分布和 z 分布。来源:https://www.geeksforgeeks.org/students-t-distribution-in-statistics/
t 分布是具有较厚尾部的正态分布。如果可用数据较少(约 30 个),则使用 t 分布代替正态分布。
在 t 分布中,自由度变量也被考虑在内。根据自由度和置信水平在 t 分布表中找到关键的 t 值。这些值用于假设检验。
t 分布表情移步:https://www.sjsu.edu/faculty/gerstman/StatPrimer/t-table.pdf。
对数正态分布
随机变量 X 的对数服从正态分布的分布。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
X = np.linspace(0, 6, 1500)
std = 1
mean = 0
lognorm\_distribution = stats.lognorm(\[std\], loc=mean)
lognorm\_distribution\_pdf = lognorm\_distribution.pdf(X)
fig, ax = plt.subplots(figsize=(8, 5))
plt.plot(X, lognorm\_distribution\_pdf, label="μ=0, σ=1")
ax.set\_xticks(np.arange(min(X), max(X)))
plt.title("Lognormal Distribution")
plt.legend()plt.show()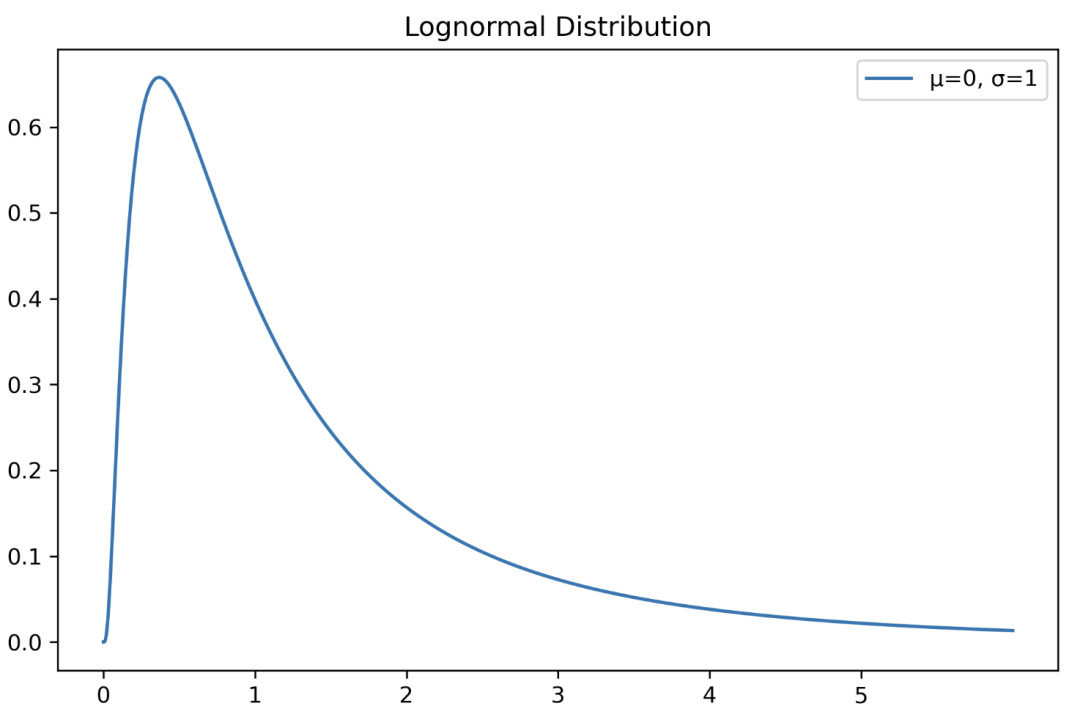
指数分布
我们在 Poisson 分布中研究了在一定时间间隔内发生的事件。在指数分布中,我们关注的是两个事件之间经过的时间。如果我们把上面的例子倒过来,那么两个电话之间需要多长时间?
因此,如果 X 是一个随机变量,遵循指数分布,则累积分布函数为:
是均值, 是常数。
from scipy.stats import expon
import matplotlib.pyplot as plt
x = expon.rvs(scale=2, size=10000) # 2 calls
# 绘图
plt.hist(x, density=True, edgecolor='black')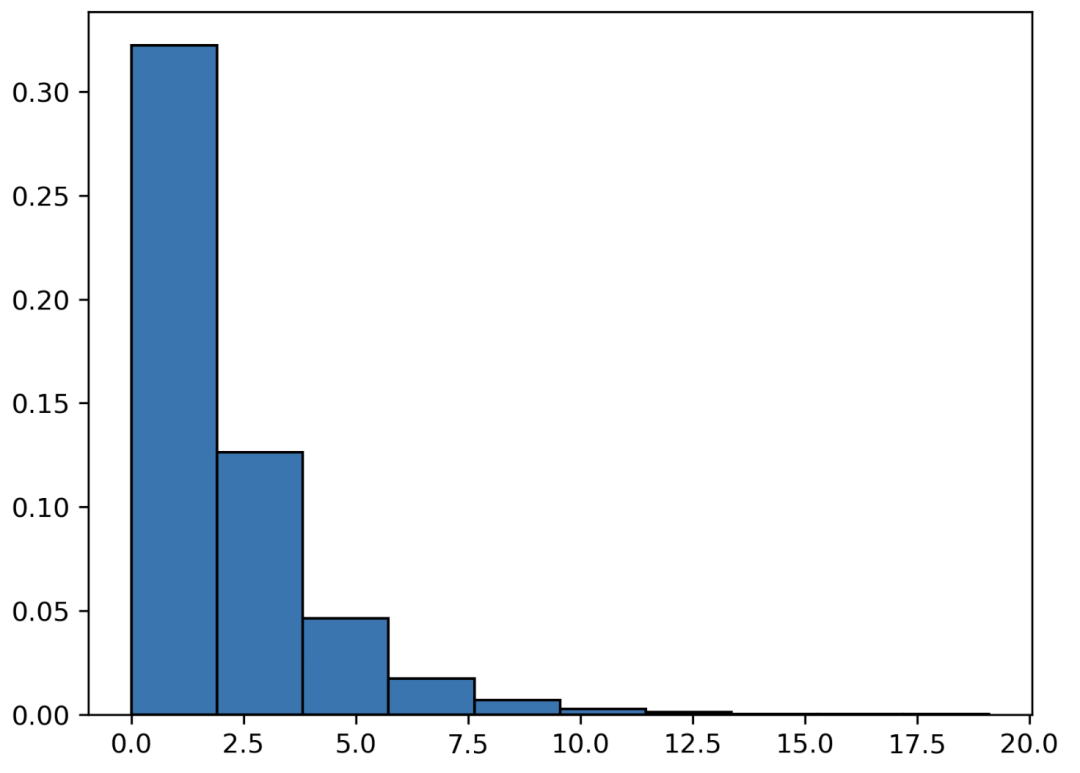
x 轴表示时间间隔的百分比。
韦伯分布
它是指时间间隔是可变的而不是固定的情况下使用的指数分布的扩展。在 Weibull 分布中,时间间隔被允许动态变化。
是形状参数,如果是正值,则事件发生的概率随时间而增加,反之亦然。 是尺度参数。
import matplotlib.pyplot as plt
x = np.arange(1,100.)/50.
def weib(x,n,a): return (a / n) \* (x / n)\*\*(a - 1) \* np.exp(-(x / n)\*\*a) count, bins, ignored = plt.hist(np.random.weibull(5.,1000))
x = np.arange(1,100.)/50.
scale = count.max()/weib(x, 1., 5.).max()
plt.plot(x, weib(x, 1., 5.)\*scale)
plt.show()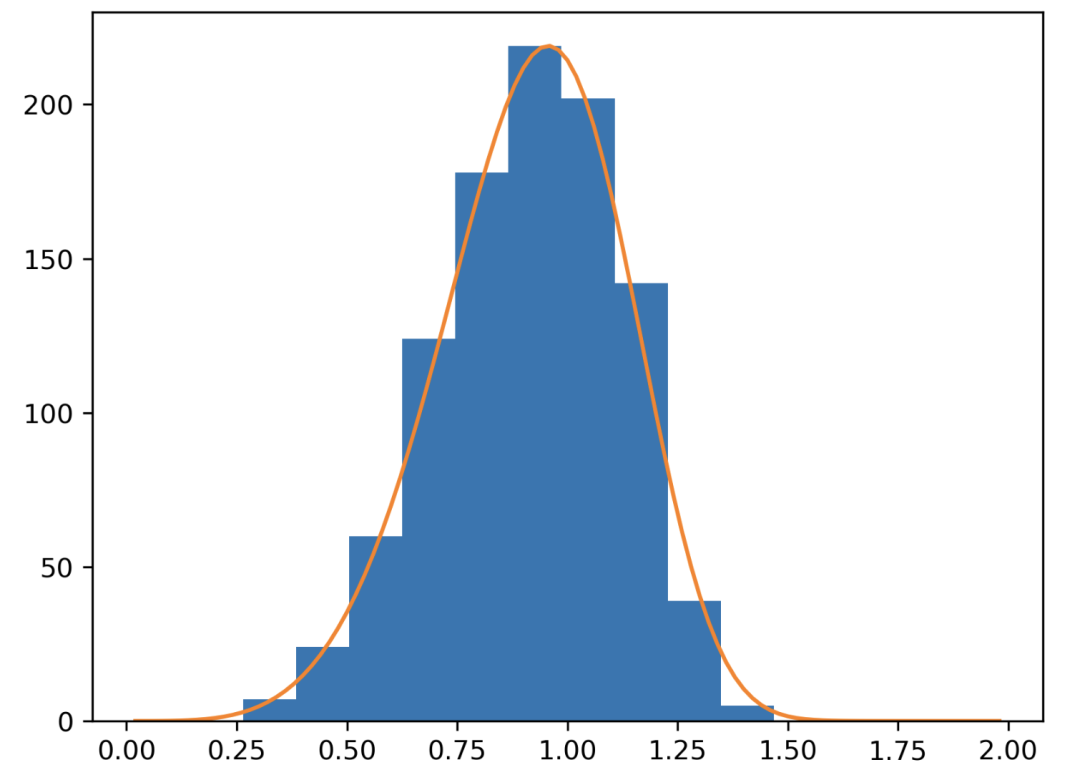
Gamma 分布
指与第 n 个事件发生所需的时间有关的分布,而指数分布则与首次事件发生的时间有关。
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
#Gamma distributions
x = np.linspace(0, 60, 1000)
y1 = stats.gamma.pdf(x, a=5, scale=3)
y2 = stats.gamma.pdf(x, a=2, scale=5)
y3 = stats.gamma.pdf(x, a=4, scale=2)
# plots
plt.plot(x, y1, label='shape=5, scale=3')
plt.plot(x, y2, label='shape=2, scale=5')
plt.plot(x, y3, label='shape=4, scale=2')
#add legend
plt.legend()
#display
plotplt.show()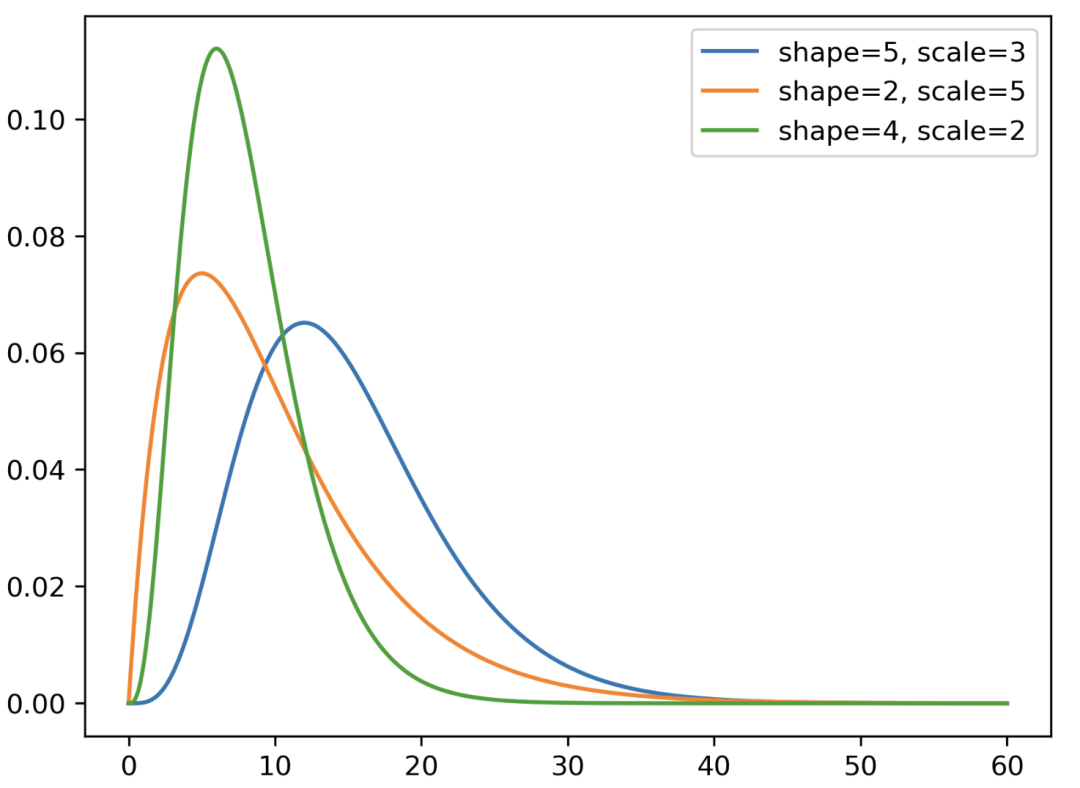
Gamma 分布。X 轴表示随机变量 X 可能取到的潜在值,Y 轴表示分布的概率密度函数(PDF)值。
Gamma 分布
它用于统计检验。这通常在实际分布中不会出现。
# x轴范围0-10,步长0.25
X = np.arange(0, 10, 0.25)
plt.subplots(figsize=(8, 5))
plt.plot(X, stats.chi2.pdf(X, df=1), label="1 dof")
plt.plot(X, stats.chi2.pdf(X, df=2), label="2 dof")
plt.plot(X, stats.chi2.pdf(X, df=3), label="3 dof")
plt.title("Chi-squared Distribution")
plt.legend()
plt.show()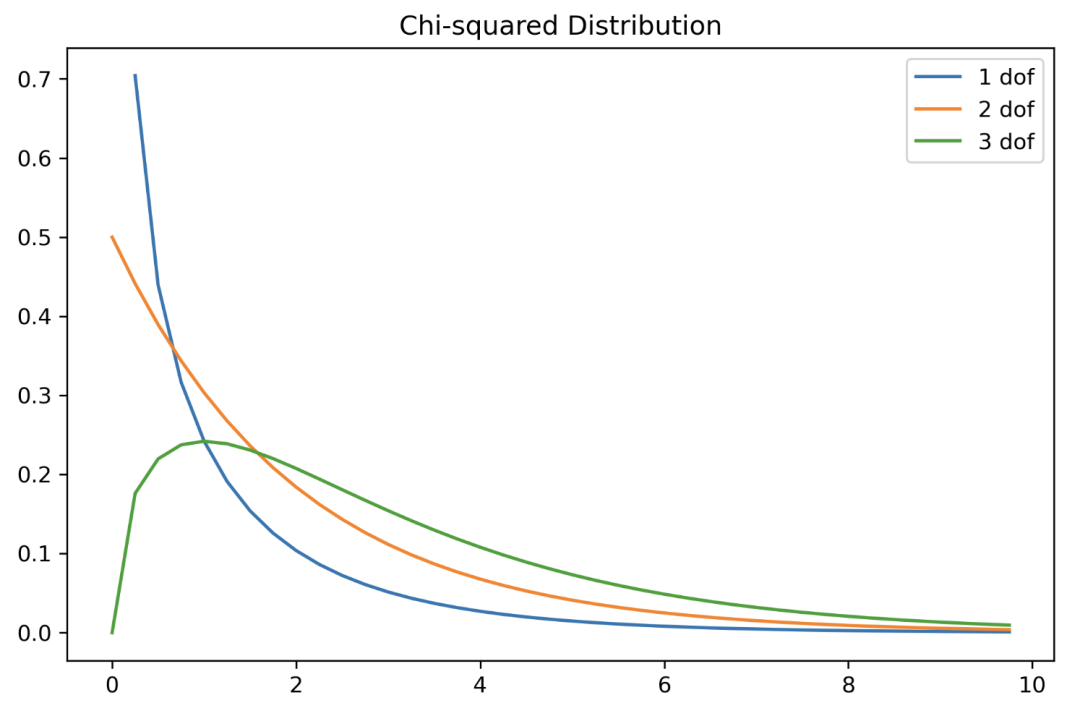
04
中心极限定理
当我们从人群中收集足够大的样本时,样本的平均值将具有正态分布,即使人群不是正态分布。
我们可以从任何分布(离散或连续)开始,从人群中收集样本并记录这些样本的平均值。随着我们继续采样,我们会注意到平均值的分布正在慢慢形成正态分布。
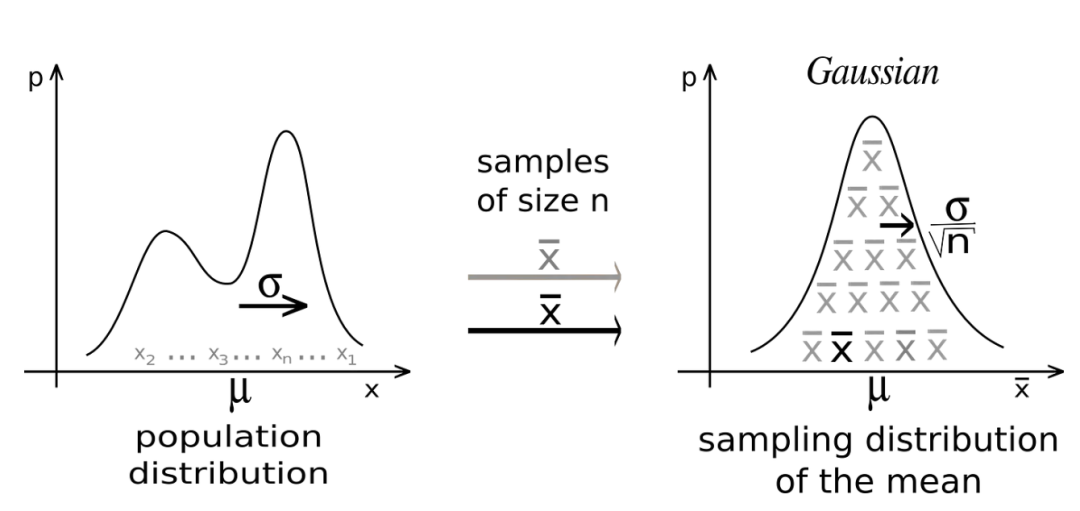
中心极限定理。来源:https://en.wikipedia.org/wiki/Central_limit_theorem
题外话

感兴趣的小伙伴,赠送全套Python学习资料,包含面试题、简历资料等具体看下方。
👉CSDN大礼包🎁:全网最全《Python学习资料》免费赠送🆓!(安全链接,放心点击)
一、Python所有方向的学习路线
Python所有方向的技术点做的整理,形成各个领域的知识点汇总,它的用处就在于,你可以按照下面的知识点去找对应的学习资源,保证自己学得较为全面。
二、Python必备开发工具
工具都帮大家整理好了,安装就可直接上手!
三、最新Python学习笔记
当我学到一定基础,有自己的理解能力的时候,会去阅读一些前辈整理的书籍或者手写的笔记资料,这些笔记详细记载了他们对一些技术点的理解,这些理解是比较独到,可以学到不一样的思路。
四、Python视频合集
观看全面零基础学习视频,看视频学习是最快捷也是最有效果的方式,跟着视频中老师的思路,从基础到深入,还是很容易入门的。
五、实战案例
纸上得来终觉浅,要学会跟着视频一起敲,要动手实操,才能将自己的所学运用到实际当中去,这时候可以搞点实战案例来学习。
六、面试宝典
简历模板
👉CSDN大礼包🎁:全网最全《Python学习资料》免费赠送🆓!(安全链接,放心点击)
若有侵权,请联系删除
![[unity]三角形顶点顺序](https://img-blog.csdnimg.cn/00190330434348ff9d9cb5d6c7ca87a0.gif)