课程链接
文章目录
- 第一周
- 1、机器学习定义
- 2、监督学习(Supervised learning)
- 1、回归(Regression)
- 2、分类(Classification)
- 3、无监督学习(Unsupervised learning)
- 4、线性回归模型
- 5、代价函数
- 6、梯度下降(Gradient descent)
- 1、学习率
- 2、用于线性回归的梯度下降
- 第二周(多维特征)
- 1、特征缩放
- 2、如何设置学习率
- 3、特征工程(Feature engineering)
- 4、多项式回归(Polynomial regression)
- 第三周
- 1、逻辑回归(二元分类)
- 2、决策边界(decision boundary)
- 3、逻辑回归中的代价函数
- 4、简化逻辑回归代价函数
- 5、实现梯度下降
- 6、过拟合问题(The Problem of Overfitting)
- 7、解决过拟合
- 8、正则化
- 9、用于线性回归的正则方法
- 10、用于逻辑回归的正则方法
第一周
1、机器学习定义

2、监督学习(Supervised learning)
从给出“正确答案”的数据集中学习
1、回归(Regression)
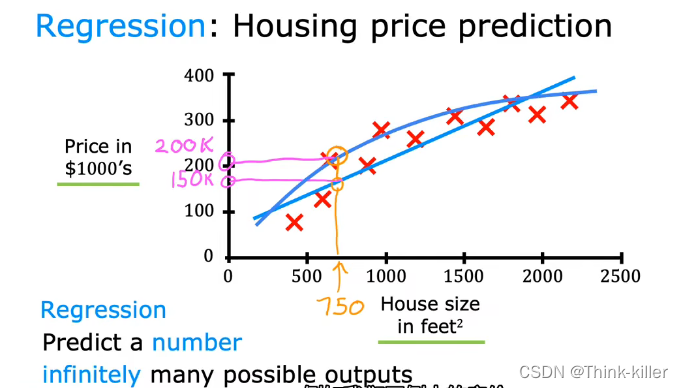
2、分类(Classification)
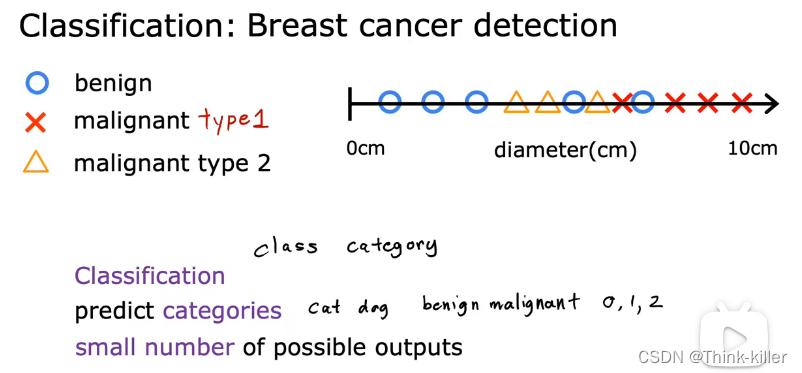
总结

3、无监督学习(Unsupervised learning)

4、线性回归模型
1.术语。

2.单变量线性回归
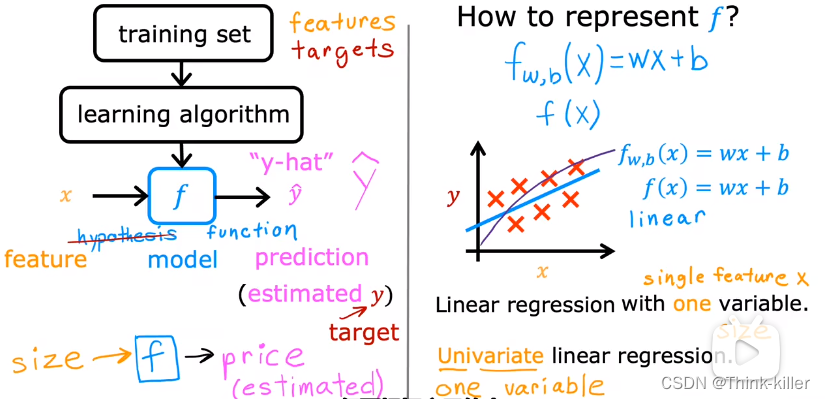
5、代价函数
平方误差代价函数
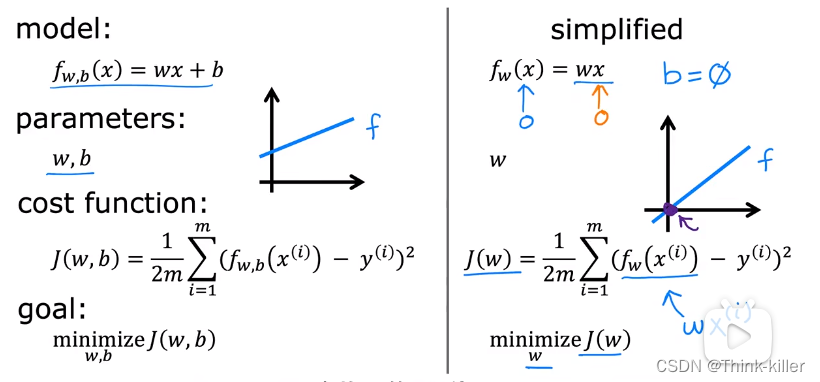
6、梯度下降(Gradient descent)
梯度下降算法选择不同的起点,可能会得到不同的结果,因为它得到的是一个局部最小值。
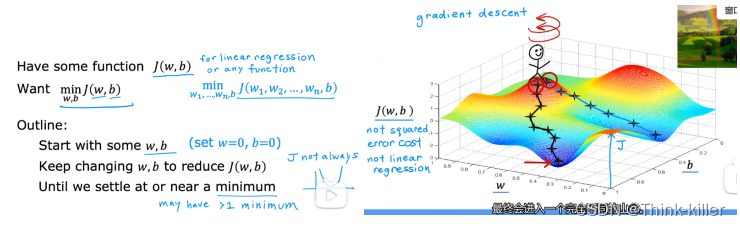

1、学习率
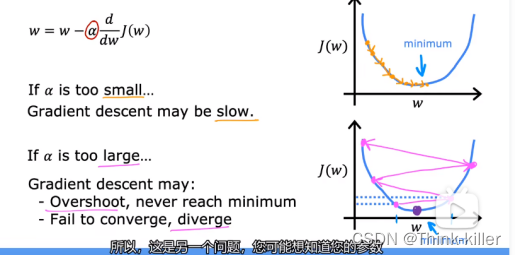
2、用于线性回归的梯度下降
线性回归的平方误差成本函数时,成本函数没有也永远不会有多个局部最小值,它只有一个全局最小值。因为这个成本函数是一个凸函数。
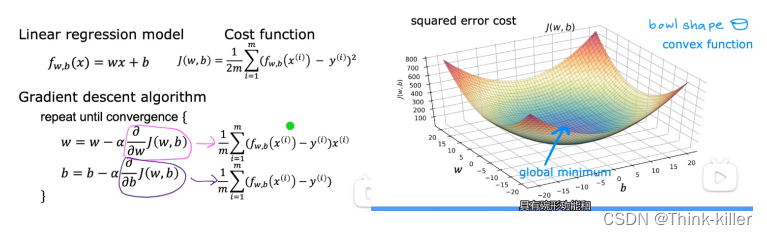
梯度下降过程
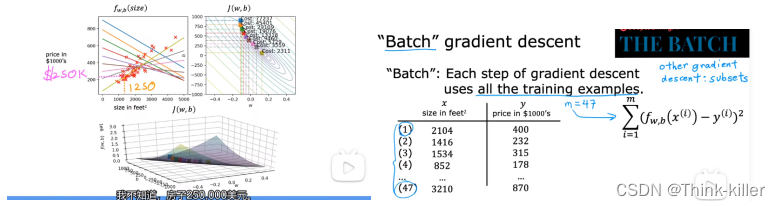
第二周(多维特征)
正规方程法(只适用于线性回归)

1、特征缩放
多个变量的度量不同,数字之间相差的大小也不同,如果可以将所有的特征变量缩放到大致相同范围,这样会减少梯度算法的迭代。
特征缩放不一定非要落到[-1,1]之间,只要数据足够接近就可以。
讨论了三种特征缩放方法:
1、每个特征除以用户选择的值,得到-1到1之间的范围。
2、Mean normalization: x i = x i − μ i m a x − m i n x_i = \frac{x_i-\mu_i}{max-min} xi=max−minxi−μi
3、Z-score normalization: X i = X i − μ i σ i X_i = \frac{X_i-\mu_i}{\sigma_i} Xi=σiXi−μi, μ i \mu_i μi表示平均值, σ i \sigma_i σi表示标准差。
特征值范围太大可能会导致梯度下降运行缓慢,所以需要进行特征缩放。

2、如何设置学习率
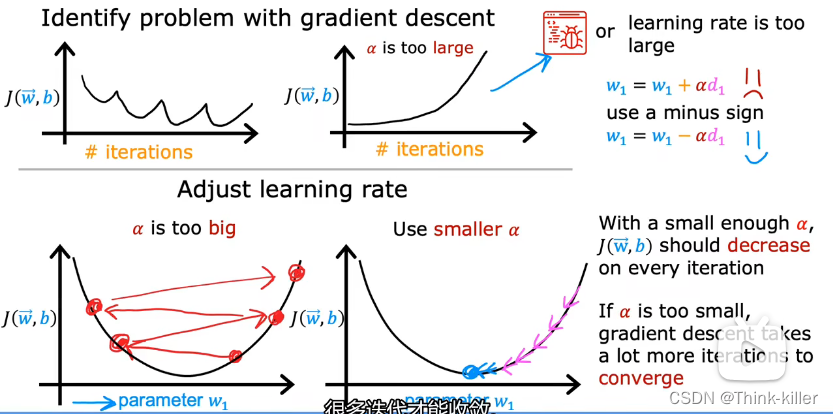
从小到大依次尝试,找到一个满足梯度下降的最大学习率。
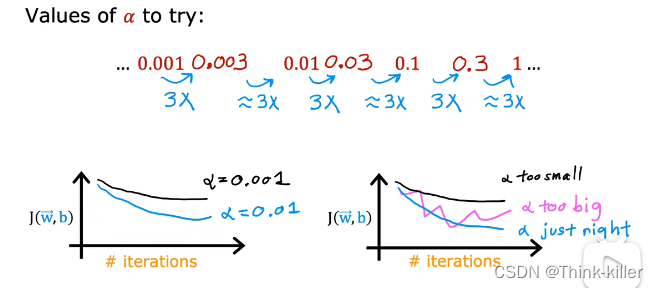
3、特征工程(Feature engineering)
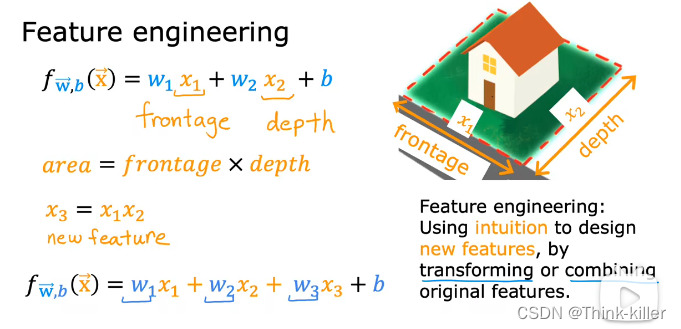
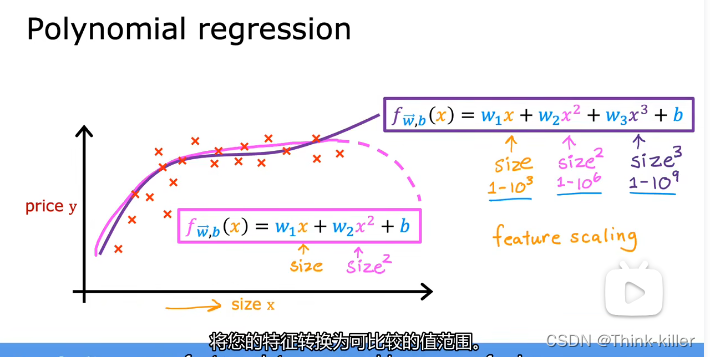
4、多项式回归(Polynomial regression)
上述讨论的都是线性回归(只有一次幂)
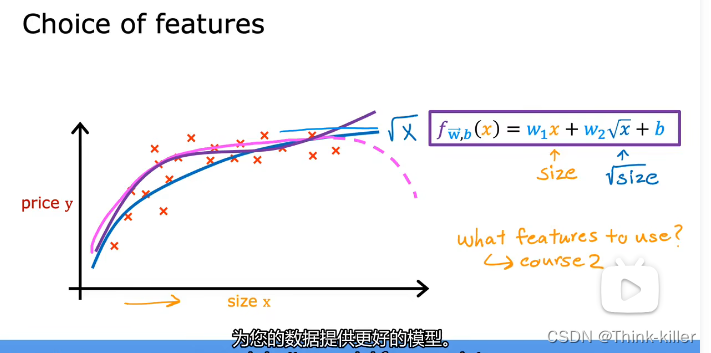
第三周
了解分类问题。
逻辑回归用于 解决y为零或一的二元分类问题。
1、逻辑回归(二元分类)
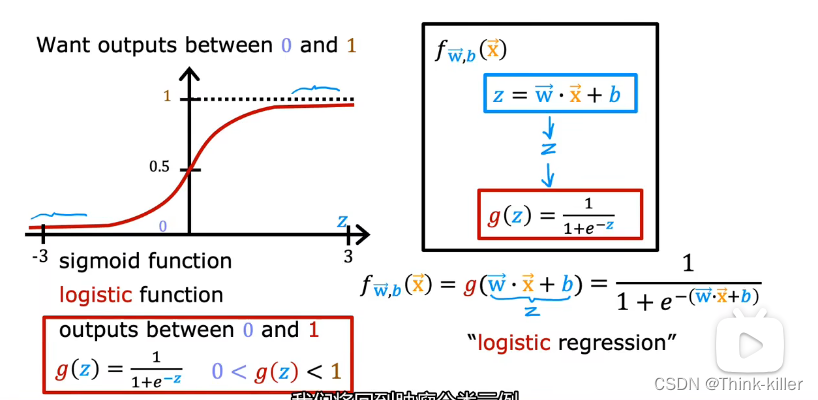

2、决策边界(decision boundary)

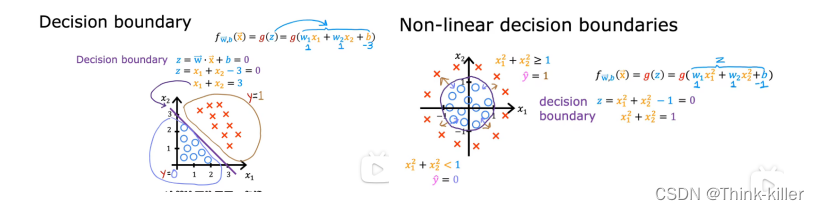
逻辑回归可以拟合相当复杂的数据

3、逻辑回归中的代价函数
事实证明,通过这种损失函数的选择,整体成本函数将是凸的,因此你可以可靠的使用梯度下降将您带到全局最小值,证明这个函数是凸的,就超过了这个代价的范围。

4、简化逻辑回归代价函数

5、实现梯度下降
逻辑回归的梯度下降
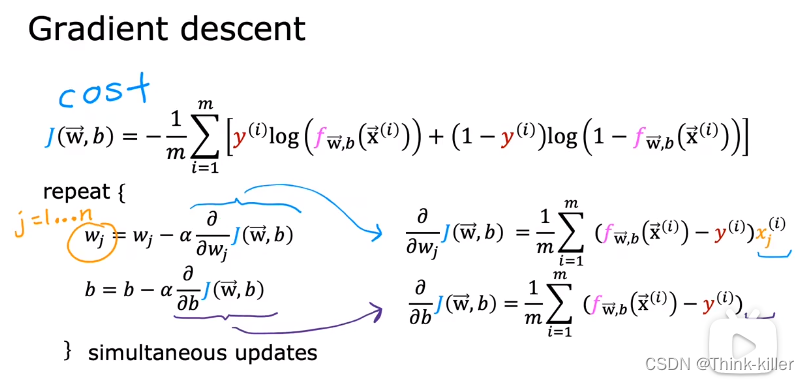

6、过拟合问题(The Problem of Overfitting)
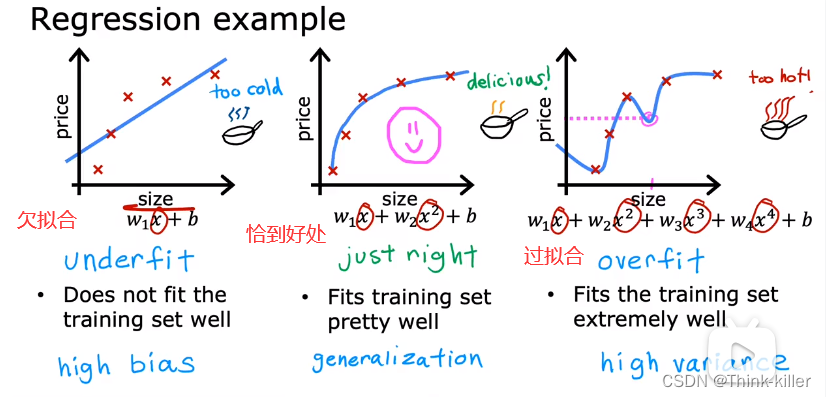
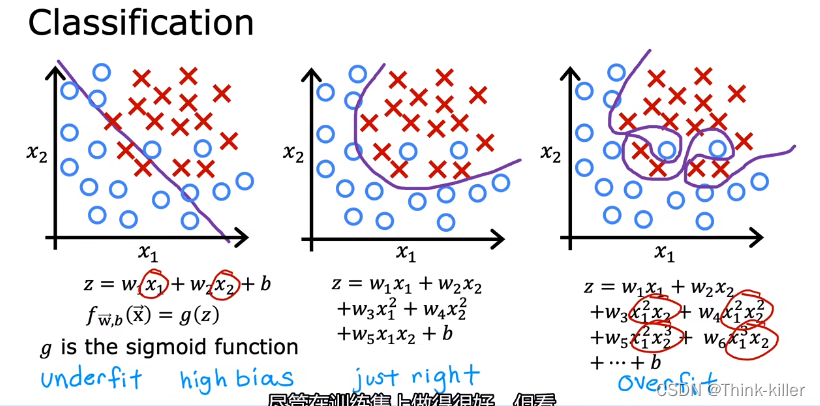
7、解决过拟合
1、对抗过度拟合的第一个工具是获取更多的训练数据。
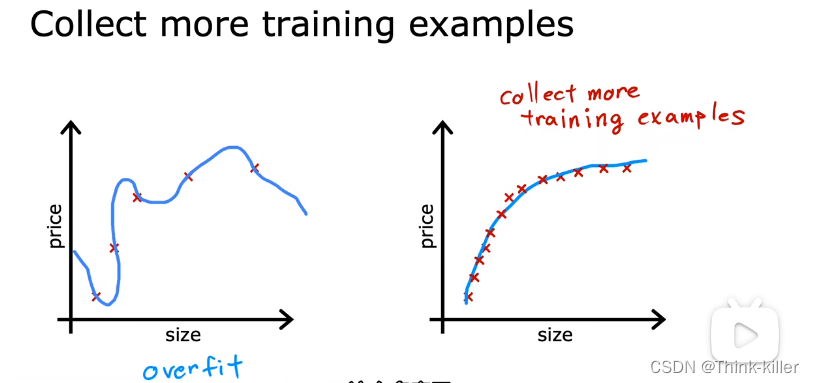
2、如果你有很多的特征,但没有足够的训练数据,那么你的学习算法也可能会过度拟合您的训练集。如果我们只选择最有用的一个特征子集,您可能发现您的模型不再过度拟合。
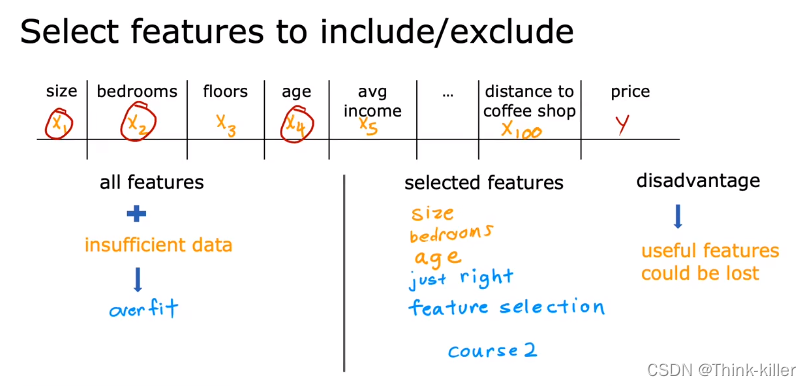
3、解决过度拟合的第三个选项----正则化
正则化的作用是让你保留所有的特征,它们只是防止特征产生过大的影响(这有时会导致过度拟合),顺便说一句,按照惯例,我们通常只是减小wj参数的大小,即w1~wn。是否正则化参数b并没有太大的区别,通常不这么做 。在实践中是否也正则化b应该没有什么区别。
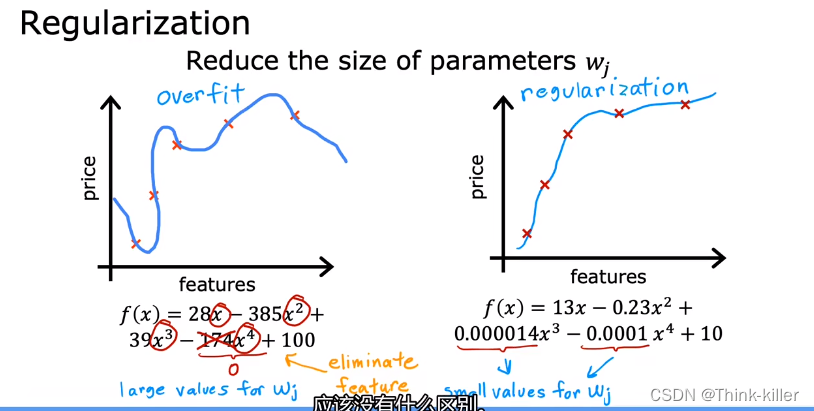

8、正则化
我们希望最小化原始成本,即均方误差成本加上额外的正则化项。所以这个新的成本函数权衡了你可能拥有的两个目标。尝试最小化第一项,并尽量减小第二项。该算法试图使参数wj保持较小,这将有助于减少过拟合。你选择的lambda值指定了相对重要性或相对权衡或你如何在这两个目标之间取得平衡。

1、如果lambda为0,您最终会拟合这条过度摆动,过于复杂的曲线,并且过度拟合。
2、如果你说lambda是一个非常非常大的数字,比如lambda=10^10,那么你对右边的这个正则化项非常重视。最小化这种情况的唯一方法是确保w的所有值都非常接近于0。因此f(x)基本等于b,因此学习算法拟合水平直线和欠拟合。
接下来的两节,将充实如何将正则化应用于线性回归和逻辑回归,以及如何通过梯度下降训练这些模型。您将能够避免这两种算法的过度拟合。
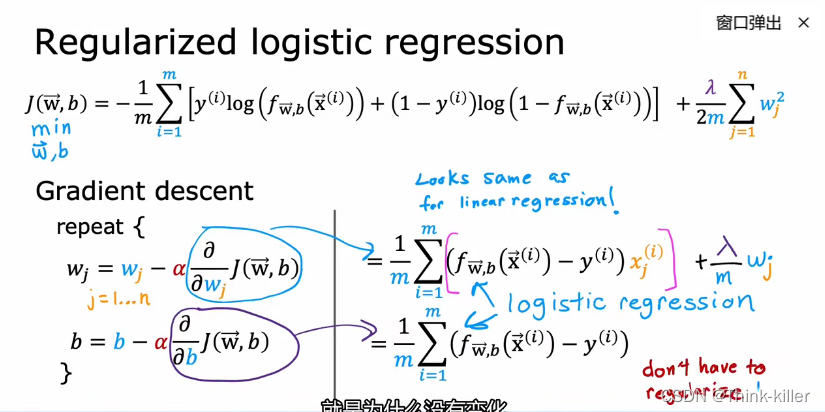
9、用于线性回归的正则方法


10、用于逻辑回归的正则方法