文章目录
- 🍀引言
- 🍀什么是梯度下降?
- 🍀损失函数
- 🍀梯度(gradient)
- 🍀梯度下降的工作原理
- 🍀梯度下降的变种
- 🍀随机梯度下降(SGD)
- 🍀批量梯度下降(BGD)
- 🍀小批量梯度下降(Mini-Batch GD)
- 🍀如何选择学习率?
- 🍀梯度下降的相关数学公式
- 🍀梯度下降的实现(代码)
- 🍀总结
🍀引言
在机器学习领域,梯度下降是一种核心的优化算法,它被广泛应用于训练神经网络、线性回归和其他机器学习模型中。本文将深入探讨梯度下降的工作原理,并且进行简单的代码实现
🍀什么是梯度下降?
梯度下降是一种迭代优化算法,旨在寻找函数的局部最小值(或最大值)以最小化(或最大化)一个损失函数。在机器学习中,我们通常使用梯度下降来最小化模型的损失函数,以便训练模型的参数。
这里顺便提一嘴,与梯度下降齐名的梯度上升算法目的是使效用函数最大。
🍀损失函数
在使用梯度下降之前,我们首先需要定义一个损失函数。损失函数是一个用于衡量模型预测值与实际观测值之间差异的函数。通常,我们使用均方误差(MSE)作为回归问题的损失函数,使用交叉熵作为分类问题的损失函数。
🍀梯度(gradient)
梯度是损失函数相对于模型参数的偏导数。它告诉我们如果稍微调整模型参数,损失函数会如何变化。梯度下降算法利用梯度的信息来不断调整参数,以减小损失函数的值。
🍀梯度下降的工作原理
梯度下降的核心思想是沿着损失函数的负梯度方向调整参数,直到达到损失函数的局部最小值。具体来说,梯度下降的步骤如下:
-
初始化模型参数:首先,随机初始化模型参数或使用某种启发式方法。
-
计算损失和梯度:使用当前模型参数计算损失函数的值,并计算损失函数相对于参数的梯度。
-
参数更新:根据梯度的方向和学习率(learning rate)本文我称其为eta,更新模型参数。学习率是一个控制步长大小的超参数,它决定了每次迭代中参数更新的大小。
-
重复迭代:重复步骤2和3,直到损失函数的值收敛到一个稳定的值,或达到预定的迭代次数。
🍀梯度下降的变种
在梯度下降的基础上,发展出了多种变种算法,以应对不同的问题和挑战。其中一些常见的包括
🍀随机梯度下降(SGD)
随机梯度下降每次只使用一个随机样本来估计梯度,从而加速收敛速度。它特别适用于大规模数据集和在线学习。
🍀批量梯度下降(BGD)
批量梯度下降在每次迭代中使用整个训练数据集来计算梯度。尽管计算开销较大,但通常能够更稳定地收敛到全局最小值。
🍀小批量梯度下降(Mini-Batch GD)
小批量梯度下降综合了SGD和BGD的优点,它使用一个小批量样本来估计梯度,平衡了计算效率和收敛性能。
🍀如何选择学习率?
学习率是梯度下降的关键超参数之一。选择合适的学习率可以加速收敛,但过大的学习率可能导致不稳定的训练过程。通常,我们可以采用以下方法选择学习率:
-
网格搜索:尝试不同的学习率值,通过验证集的性能来选择最佳值。
-
学习率衰减:开始时使用较大的学习率,随着训练的进行逐渐减小学习率。
-
自适应学习率:使用自适应学习率算法,如Adam、Adagrad或RMSprop,它们可以自动调整学习率以适应梯度的变化。
🍀梯度下降的相关数学公式
本人数学不好,这里有说的不清楚的地方还请见谅,谢谢佬~
首先我们通过图像认识一下损失函数
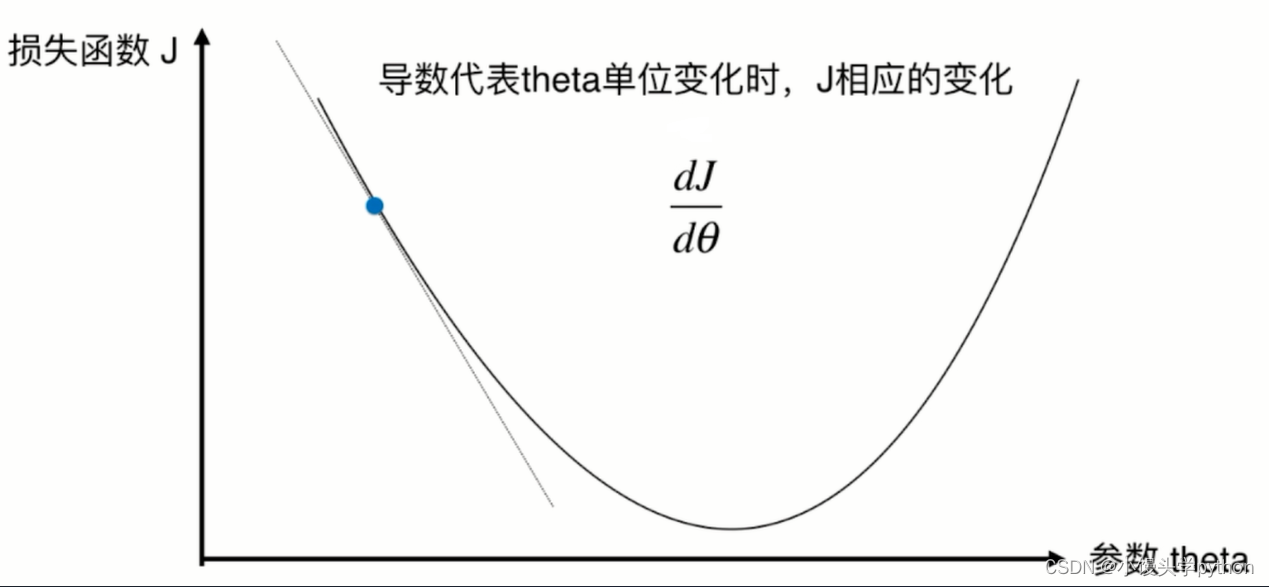
这里的步长指的是,可能有些人会好奇为啥有一个负号呢?因为对称轴左侧的导数都是负值,这里加一个负号不就正了嘛
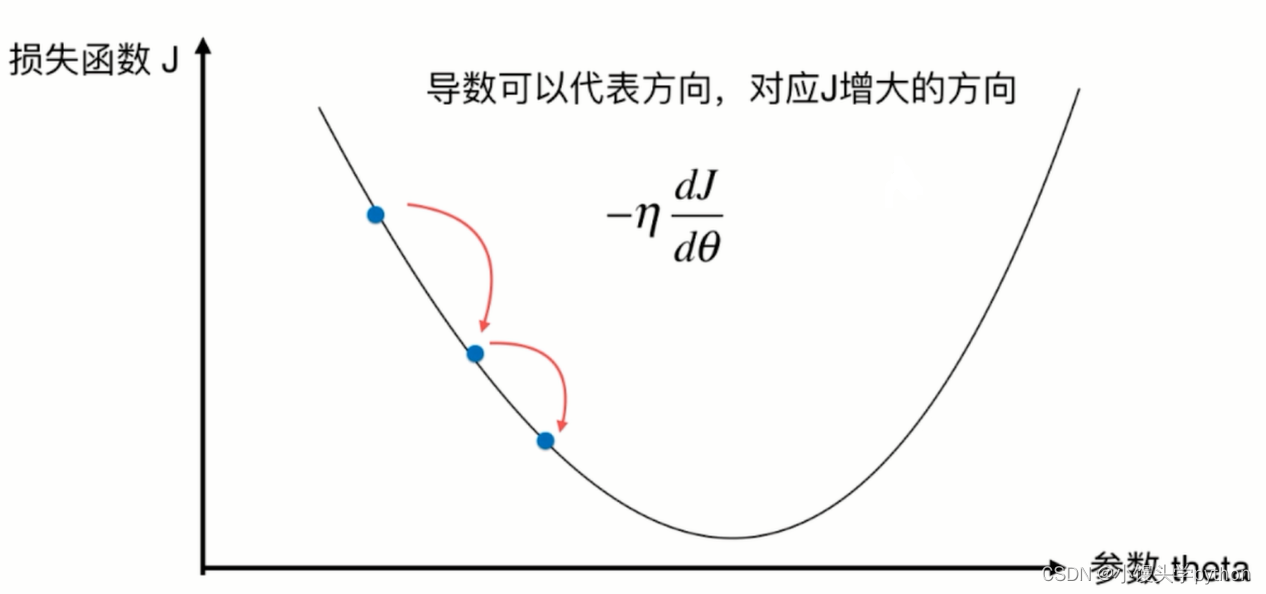
具体推导过程请查看相关佬的文章(哭~)
🍀梯度下降的实现(代码)
首先我们导入我们需要的库
import numpy as np
import matplotlib.pyplot as plt
之后我们需要举一个例子,这里我们采用numpy里面的一个分割函数linspace,同时我们举一个函数的例子
plt_x = np.linspace(-1,6,141)
plt_y = (plt_x-2.5)**2-1
之后我们使用show进行展示一下图像
plt.plot(plt_x,ply_y)
plt.show()
运行结果如下
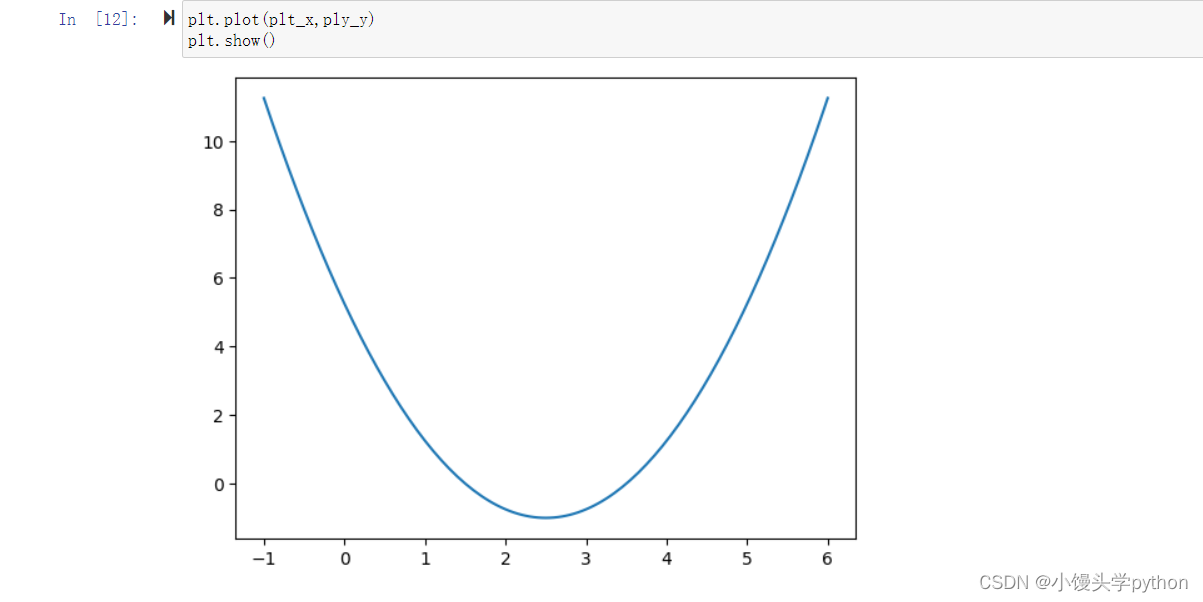
上图看起来就是一个普通的曲线,方便我们进行理解
接下来我们需要两个函数,一个为了返回导数,一个为了返回对应的y值
def dj(thera):return 2*(thera-2.5) # 求导
def j(thera)return (thera-2.5)**2-1 # 求对应的值
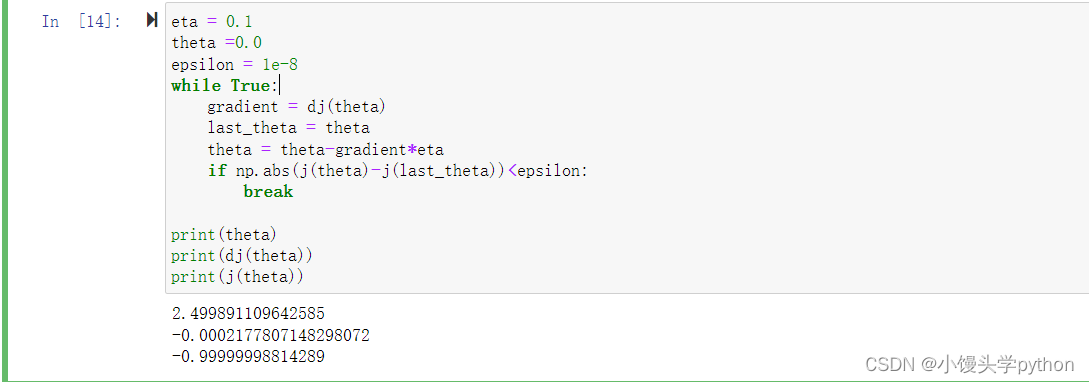
接下来是梯度下降的关键位置了,这里我们需要初始化两个参数以及一个范围参数,同时设置一个while循环,将前一个thera保存在last_thera中,后一个thera是前一个thera和步长的差值,这里的步长就是梯度个参数eta的乘积,最后使用if函数来终结循环,最终我们将最小值点的值、导数、以及自变量打印出来
eta = 0.1
theta =0.0
epsilon = 1e-8
while True:gradient = dj(theta)last_theta = thetatheta = theta-gradient*eta if np.abs(j(theta)-j(last_theta))<epsilon:breakprint(theta)
print(dj(theta))
print(j(theta))
运行结果如下
这里我们也可以使用列表来看看到底进行了多少次thera的循环
eta = 0.1
theta =0.0
epsilon = 1e-8
theta_history = [theta]
while True:gradient = dj(theta)last_theta = thetatheta = theta-gradient*eta theta_history.append(theta)if np.abs(j(theta)-j(last_theta))<epsilon:breakprint(theta)
print(dj(theta))
print(j(theta))len(theta_history)
运行结果如下

还可以绘制图像进行直观查看
plt.plot(plt_x,plt_y)
plt.plot(theta_history,[(i-2.5)**2-1 for i in theta_history],color='r',marker='*')
plt.show()
运行结果如下
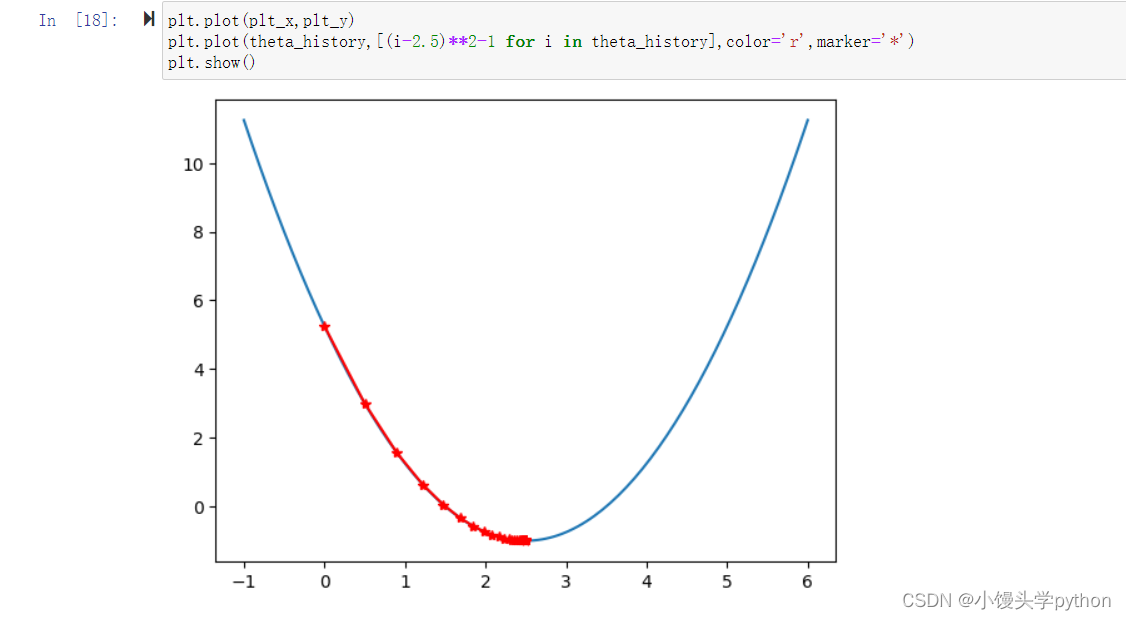
这样的话就很直观了吧~
🍀总结
本节只介绍梯度下降的简单实现,下节继续学习此法中eta参数的调节

挑战与创造都是很痛苦的,但是很充实。


![[羊城杯 2020] easyphp](https://img-blog.csdnimg.cn/395d26e7cac8482fbe81dcc57860044c.png)