1.向量的概念
定义:
既有大小,又有方向。
向量的表示法
记有向线段的起点A与终点B,从点A指向B的箭头表示了这条线端的方向,线段的长度表示了这条线段的大小,向量就可用这样的一条有向线段来表示,
记作:
A B ⃗ \vec{AB} AB
向量也可以简记为:
α β γ \alpha \quad \beta \quad \gamma αβγ …等
将向量的长度记为:
| A B ⃗ \vec{AB} AB| 简称为:模
2. 特殊的向量
(1) 单位向量: 模为1的向量;与向量 a ⃗ \vec{a} a同方向的单位向量。
(2)零向量:模为0的向量,记作: 0 ⃗ \vec{0} 0,规定零向量的方向是任意的方向。
3.向量的关系
(1)向量平行 对于两个非零向量 a ⃗ \vec{a} a, b ⃗ \vec{b} b,若它们的方向相同或相反,则称这两个向量平行或共线,记作 a ⃗ \vec{a} a// b ⃗ \vec{b} b。
(2)向量相等 若两个向量 a ⃗ \vec{a} a, b ⃗ \vec{b} b的模相等且方向相同,则称这两个向量相等,记作 a ⃗ \vec{a} a= b ⃗ \vec{b} b。
注:
(1)零向量与任何向量都是平行关系;
(2)若某向量可以在空间中平行移动,所得向量与原向量相等,则称该向量为自由向量。
4.向量的加法
(1)平行四边形法则
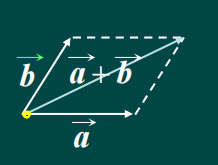
(2)三角形法则
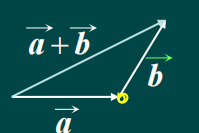
(3)三棱锥法则
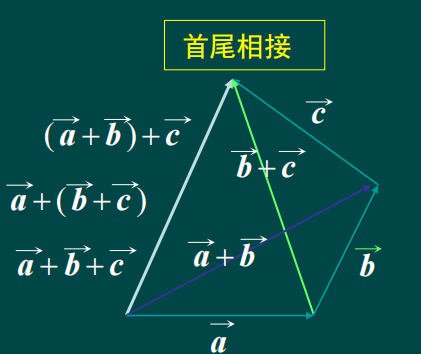
加法运算规律:
交换律
a ⃗ \vec{a} a+ b ⃗ \vec{b} b= b ⃗ \vec{b} b+ a ⃗ \vec{a} a
结合律:
( a ⃗ \vec{a} a+ b ⃗ \vec{b} b)+ c ⃗ \vec{c} c = a ⃗ \vec{a} a+( b ⃗ \vec{b} b+ c ⃗ \vec{c} c) = a ⃗ \vec{a} a+ b ⃗ \vec{b} b+ c ⃗ \vec{c} c
三角形法则可推广到多个向量相加。
向量的减法
a ⃗ \vec{a} a- b ⃗ \vec{b} b= a ⃗ \vec{a} a+(- b ⃗ \vec{b} b)
特别是 a ⃗ \vec{a} a= b ⃗ \vec{b} b的时候
a ⃗ \vec{a} a- b ⃗ \vec{b} b=0
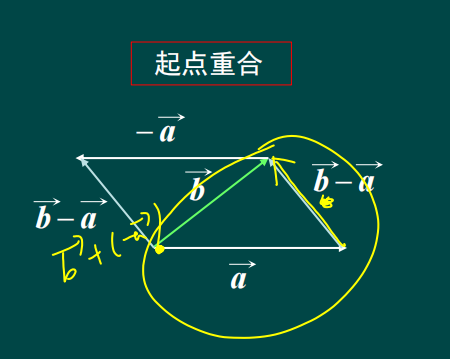
三角不等式
| a ⃗ \vec{a} a+ b ⃗ \vec{b} b| ≤ \leq ≤ | a ⃗ \vec{a} a|+|- b ⃗ \vec{b} b|
| a ⃗ \vec{a} a- b ⃗ \vec{b} b| ≤ \leq ≤ | a ⃗ \vec{a} a|-| b ⃗ \vec{b} b|
向量与数的乘法
设是一实数, λ 与的乘积是一新向量,记作 λ a ⃗ \lambda与 的乘积是一新向量,记作\lambda\vec{a} λ与的乘积是一新向量,记作λa 。
模长为:
| λ a ⃗ ∣ = ∣ λ ∣ ∣ a ⃗ \lambda \vec{a} |= |\lambda|| \vec{a} λa∣=∣λ∣∣a|
数乘法运算律:
结合律
λ ( μ α ) = λ μ α = μ ( λ α \lambda(\mu\alpha)= \lambda\mu\alpha = \mu(\lambda\alpha λ(μα)=λμα=μ(λα)
分配律
λ ( a ⃗ + b ⃗ ) = λ a ⃗ + λ b ⃗ \lambda(\vec{a}+\vec{b})=\lambda\vec{a}+\lambda\vec{b} λ(a+b)=λa+λb
λ a ⃗ + λ b ⃗ = λ ( a ⃗ + b ⃗ \lambda\vec{a}+\lambda\vec{b}= \lambda(\vec{a}+\vec{b} λa+λb=λ(a+b)
若向量 a ⃗ \vec{a} a ≠ 0 ⃗ \neq\vec{0} =0,
则其单位向量为 a ⃗ = 1 ∣ a ⃗ ∣ a ⃗ \vec{a} = \frac{1}{|\vec{a}|}\vec{a} a=∣a∣1a
向量的夹角
设有两个向量 a ⃗ \vec{a} a, b ⃗ \vec{b} b平移致使始点重合,且交于点S。把一个向量绕点S在两个向量所确定的平面上旋转,直到方向和另一个向量的方向重合,则称所旋转的角度为向量 a ⃗ \vec{a} a, b ⃗ \vec{b} b 的夹角, ϑ \vartheta ϑ=(<a,b)记作 ,其中 ϑ ∈ \vartheta\in ϑ∈[0, π \pi π]。
特殊的向量夹角
- ϑ \vartheta ϑ = 0 ⟵ \longleftarrow ⟵ ⟶ \longrightarrow ⟶ 向量 a ⃗ \vec{a} a, b ⃗ \vec{b} b平行,且方向相同;
- ϑ \vartheta ϑ = π \pi π $ \longleftarrow$ ⟶ \longrightarrow ⟶ 向量 a ⃗ \vec{a} a, b ⃗ \vec{b} b平行,且方向相反;
- ϑ \vartheta ϑ = π 2 \frac{\pi}{2} 2π ⟵ \longleftarrow ⟵ ⟶ \longrightarrow ⟶ 向量 a ⃗ \vec{a} a, b ⃗ \vec{b} b垂直,记作 a ⃗ ⊥ b ⃗ \vec{a}\bot\vec{b} a⊥b;
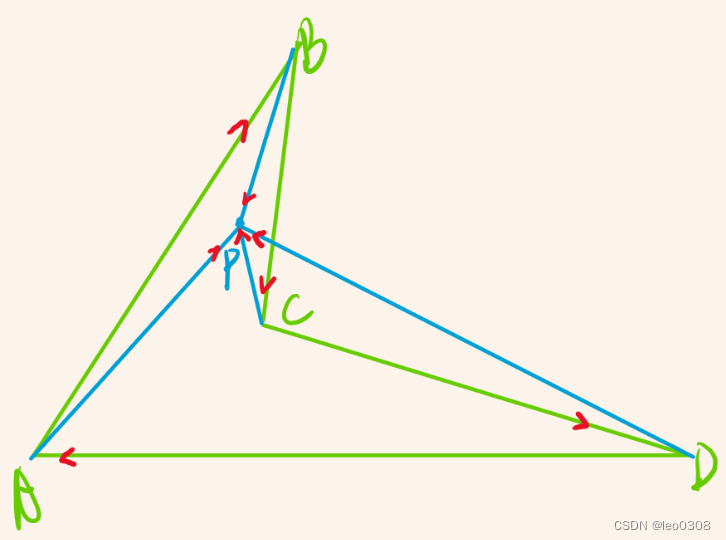
向量的投影
(1)点在数轴上的投影 已知空间一点M与一数轴u ,过点M 作垂直于数轴u的平面 β \beta β,且交点为M′ ,则称点M′为点M在数轴u上的投影,其中数轴u称为投影轴。
(2)向量的投影 设向量𝐶的始点C和终点D在数轴u上的投影点分别是C ′为D ′ ,则称向量 C ′ D ′ ⃗ \vec{C′D′} C′D′为向量CD的投影向量。记 P r j u C D ⃗ Prju \vec{CD} PrjuCD = C′ − D′。
图示:

向量投影的计算
定理1 对于任意非零向量 α \alpha α,有
P r j u α = ∣ α ∣ cos φ Prju \alpha = |\alpha|\cos\varphi Prjuα=∣α∣cosφ
其中 φ \varphi φ是 α \alpha α与数轴 u u u的夹角。
注:(1)当投影轴与向量成锐角时,向量的投影为正;
当投影轴与向量成钝角时,向量的投影为负;
当投影轴与向量成直角时,向量的投影为零。
(2)相等的向量在同一数轴上的投影相等。
定理2: 投影的线性性质 (1) P r j u ( α ± β ) = P r j u α ± P r j u β Prju (\alpha \pm \beta) = Prju\alpha \pm Prju\beta Prju(α±β)=Prjuα±Prjuβ
(2) P r j u ( λ α ) = λ P r j u α Prju(\lambda\alpha) = \lambda Prju \alpha Prju(λα)=λPrjuα
向量的坐标
定义3 设向量 i ⃗ , j ⃗ , k ⃗ \vec{i},\vec{j},\vec{k} i,j,k分别为与x,y,z轴同向的单位向量,则称其为
空间直角坐标系的基本单位向量。
定义4 向径的坐标表示设点M的坐标为(x,y,z ),则向径 r =OM= (x,y,z )
r = x i + y j + z k r = xi + yj + zk r=xi+yj+zk
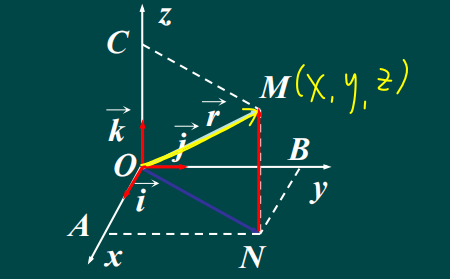
定义 若向量 α \alpha α分别在x,y,z轴上的投影 α x , α y , α z \alpha x,\alpha y,\alpha z αx,αy,αz组成的有序数组( α x , α y , α z \alpha x,\alpha y,\alpha z αx,αy,αz)为向量 α \alpha α的坐标,记为 α = ( α x , α y , α z ) \alpha=(\alpha x,\alpha y,\alpha z) α=(αx,αy,αz)
定义4 设始点M1 (x1,y1,z1) ,终点M2 (x2,y2,z2) ,因此 M 1 M 2 ⃗ \vec{M1M2} M1M2的坐标为 ( x 2 − x 1 , y 2 − y 1 , z 2 − z 1 ) (x2-x1,y2-y1,z2-z1) (x2−x1,y2−y1,z2−z1)
且分解式表达为 M 1 M 2 ⃗ = ( x 2 − x 1 ) i ⃗ + ( y 2 − y 1 ) y ⃗ + ( z 2 − z 1 ) z ⃗ \vec{M1M2}= (x2-x1)\vec{i}+(y2-y1)\vec{y}+(z2-z1)\vec{z} M1M2=(x2−x1)i+(y2−y1)y+(z2−z1)z
(1) 计算向量的模 α = ( α x , α y , α z ) \alpha = (\alpha x,\alpha y,\alpha z) α=(αx,αy,αz)
∣ α ∣ = α x 2 + α y 2 + α z 2 |\alpha| = \sqrt{\alpha x^2+\alpha y^2+\alpha z^2} ∣α∣=αx2+αy2+αz2
(2)向量的方向角
若向量 α \alpha α与下,x,y,z轴正向的夹角分别为 α , β , γ \alpha,\beta,\gamma α,β,γ,则称 α , β , γ \alpha,\beta,\gamma α,β,γ为方向量 α \alpha α在x,y,z,轴方向角。 cos α , cos β , cos γ \cos\alpha,\cos\beta,\cos\gamma cosα,cosβ,cosγ分别称为方向余弦。
且有:
α x = ∣ α ∣ cos α , α y = ∣ α ∣ cos β , α z = ∣ α ∣ cos γ \alpha x =|\alpha|\cos\alpha,\alpha y = |\alpha|\cos\beta,\alpha z = |\alpha|\cos\gamma αx=∣α∣cosα,αy=∣α∣cosβ,αz=∣α∣cosγ
以及有:
cos 2 α + cos 2 β + cos 2 γ = 1 \cos^2 \alpha+\cos^2 \beta + \cos^2 \gamma = 1 cos2α+cos2β+cos2γ=1
向量坐标运算
设 a = ( a x , a y , a z ) , β = ( b x , b y , b z ) a = (ax,ay,az) , \beta = (bx,by,bz) a=(ax,ay,az),β=(bx,by,bz)
则 α ± β = ( a x ± b x , a y ± b y , a z ± b z ) \alpha \pm \beta = (ax \pm bx,ay \pm by,az \pm bz) α±β=(ax±bx,ay±by,az±bz)
λ α = ( λ a x , λ a y , λ a z ) λ ∈ R \lambda\alpha = (\lambda ax,\lambda ay, \lambda az) \lambda \in R λα=(λax,λay,λaz)λ∈R
向量坐标运算
设 a = ( a x , a y , a z ) , β = ( b x , b y , b z ) a = (ax,ay,az) , \beta = (bx,by,bz) a=(ax,ay,az),β=(bx,by,bz)
则 α ± β = ( a x ± b x , a y ± b y , a z ± b z ) \alpha \pm \beta = (ax \pm bx,ay \pm by,az \pm bz) α±β=(ax±bx,ay±by,az±bz)
λ α = ( λ a x , λ a y , λ a z ) λ ∈ R \lambda\alpha = (\lambda ax,\lambda ay, \lambda az) \lambda \in R λα=(λax,λay,λaz)λ∈R




![微服务[Nacos]](https://img-blog.csdnimg.cn/067558d0fad3498d9e334ceb98d078b1.png)