1.前言

几乎在每一个系统的开发过程中，都会遇到一些树状结构的开发需求，例如：组织机构树，部门树，菜单树等。只要是需要开发这种树状结构的需求，我们都可以使用组合模式来完成。

本篇将结合组合模式与Mysql实现一个部门树，完成其增删改和树形结构的组装。

2.组合模式

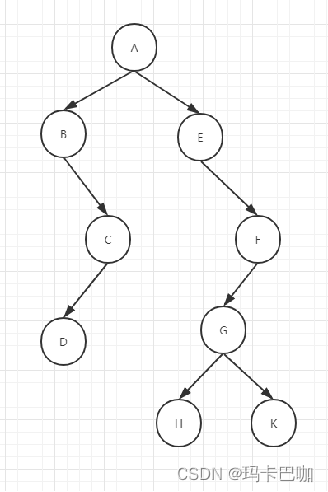
组合模式是一种结构型设计模式，它允许我们将对象组合成树形结构来表现部分-整体的层次结构。以部门树为例，我们可以将上级部门与下级部门组合起来，形成一个单边树，用代码来描述的话，就是这个样子的：

public class DeptNode {private List<DeptNode> children = new ArrayList<>();
}

提供一个部门节点类，里面会有一个集合，用于保存当前部门的下级部门，同理在children这个集合中的部门节点，也可能会有它的下级部门节点。

当然，这不是实现组合模式的唯一方式，还有其他复杂一点方式，会区分不同的节点类型，是根节点、分支节点、还是叶子节点等。这里之所以做这种简单的设计，是因为我们的树状结构的数据一般都会交给前端去做渲染，在很多前端的组件库中，就是用这种简单的方式来组织树的，例如在Element-UI中的树状结构：

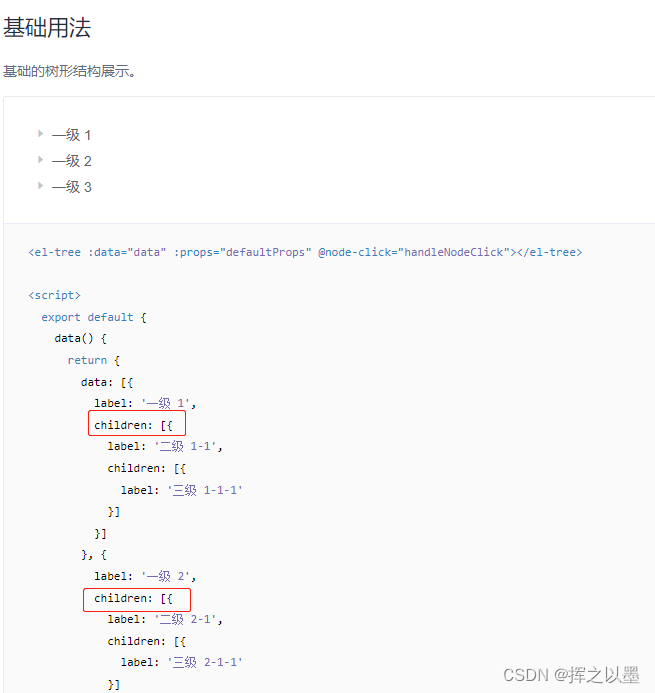
3.实现方式

3.1.数据结构设计

先看数据库的设计，数据库必要的字段比较简单，直接看一下建表的sql：

create table dept
(id        bigint auto_increment comment '部门id'primary key,parent_id bigint       null comment '上级部门id',name      varchar(200) null comment '部门名称',tree_path varchar(255) null comment '树路径'
)

id与parent_id很好理解，主要是用来维护部门的上下级关系，name不解释，tree_path这个字段其实不是必须要的，没有它也可以实现部门树，但是加上这个path之后，可以比较方便的查询子树。

---

PO对象与数据库字段保持一致，这里就不过多赘述，代码中需要返回给前端的树对象要修改一下字段名，name->label：

@Getter
@Setter
public class DeptNode {private List<DeptNode> children = new ArrayList<>();private Long id;private Long parentId;private String label;private String treePath;
}

3.2.数据新增

由于是自增主键，数据的新增需要再保存之后获取到主键id，再更新treePath。
这里为了方便，我用了dept对象直接透传，使用的是mybatis-plus操作数据库，可以替换成自己喜欢的ORM。

@Service("deptService")
public class DeptServiceImpl extends ServiceImpl<DeptDao, Dept> implements DeptService {@Override@Transactional(rollbackFor = Exception.class)public void insert(Dept dept) {// 如果有上级部门id，则获取上级机构Dept parentDept = null;if (dept.getParentId() != null) {parentDept = this.getById(dept.getParentId());// 上级机构不能为空if (parentDept == null) {throw new RuntimeException("上级机构不存在");}}// MybatisPlus新增后可以获取主键this.save(dept);// 更新树路径if (parentDept != null) {dept.setTreePath(parentDept.getTreePath() + dept.getId() + "/");} else {dept.setTreePath("/" + dept.getId() + "/");}this.updateById(dept);}
}

3.2.数据更新

数据更新需要注意两个点：

• 新的上级部门不能是自己，也不能是自己的子部门（避免成环）。
• 更新树路径之后，树路径上的所有子部门都需要更新树路径。

@Override
@Transactional(rollbackFor = Exception.class)
public void update(Dept dept) {Dept newParentDept = null;if (dept.getParentId() != null) {newParentDept = this.getById(dept.getParentId());if (newParentDept == null) {throw new RuntimeException("上级部门不存在");}if (newParentDept.getTreePath().contains("/" + dept.getId() + "/")) {throw new RuntimeException("上级部门不能是自己或子部门");}}this.updateById(dept);// 组装新的树路径String newTreePath = (newParentDept == null ? "" : newParentDept.getTreePath()) + dept.getId() + "/"; + dept.getId() + "/";// 获取原有的树路径String oldTreePath = this.getById(dept.getId()).getTreePath();// 获取所有子部门（循环更新也可以替换为使用Mysql的replace函数批量更新）LambdaQueryWrapper<Dept> queryWrapper = new LambdaQueryWrapper<>();// likeRight表示右模糊查询，即以oldTreePath开头的queryWrapper.likeRight(Dept::getTreePath, oldTreePath);this.list(queryWrapper).forEach(childDept -> {// 更新子部门的树路径childDept.setTreePath(childDept.getTreePath().replace(oldTreePath, newTreePath));this.updateById(childDept);});
}

上面的循环更新在数据量不大的时候可以这么做，如果量较大的话，推荐使用mysql中的replace函数替换：

update dept set tree_path = replace(tree_path,'旧路径','新路径')
where tree_path like '旧路径%'

把sql中的旧路径，新路径替换为上面代码中获取到的路径即可。

3.4.部门树组装

部门树组装只需要把需要组装的部门列表查询出来，然后根据parent_id的关联关系组装数据即可。这里tree_path就可以派上用场了，如果只有parent_id的话，要么必须全量查询所有的部门再过滤，要么需要根据parent_id做递归查询，而通过tree_path可以直接做右模糊查询，查询到的部门都是需要的部门。

我们可以在接口中接收一个部门的id，把这个部门作为部门子树的根节点：

@Override
public List<DeptNode> tree(Long id) {// 传入了主键id，则通过主键id对于treePath做右模糊查询，没有传入主键id，则查询所有List<Dept> list;if (id != null) {Dept baseDept = this.getById(id);list = this.list(new LambdaQueryWrapper<Dept>().likeRight(Dept::getTreePath, baseDept.getTreePath()));} else {list = this.list();}// 将Dept转换为DeptNodeList<DeptNode> deptNodes = new ArrayList<>();for (Dept dept : list) {DeptNode deptNode = BeanUtil.copyProperties(dept, DeptNode.class);deptNode.setLabel(dept.getName());deptNodes.add(deptNode);}// 循环遍历，将子节点放入父节点的children中for (DeptNode node : deptNodes) {deptNodes.stream().filter(item -> node.getId().equals(item.getParentId())).forEach(item -> {if (node.getChildren() == null) {node.setChildren(CollUtil.newArrayList(item));} else {node.getChildren().add(item);}});}// 返回根节点return deptNodes.stream().filter(item -> item.getParentId() == null || item.getId().equals(id)).collect(Collectors.toList());
}

4.测试

通过一个Controller接口发起测试：

@RestController
@RequestMapping("dept")
public class DeptController {@Resourceprivate DeptService deptService;@PostMapping("insert")public void insert(@RequestBody @Valid Dept dept) {this.deptService.insert(dept);}@PostMapping("update")public void update(@RequestBody @Valid Dept dept) {this.deptService.update(dept);}@PostMapping("/tree")public List<DeptNode> tree(Long id) {return this.deptService.tree(id);}
}

4.1.部门新增

按照下面的请求参数顺序发起insert请求，为了验证的方便，这里的部门加了数字后缀：

{"parentId": null,"name": "根部门"
}
{"parentId": 1,"name": "一级部门-1"
}
{"parentId": 1,"name": "一级部门-2"
}
{"parentId": 2,"name": "二级部门-1-1"
}
{"parentId": 3,"name": "二级部门-2-1"
}
{"parentId": 5,"name": "三级部门-2-1-1"
}
{"parentId": 5,"name": "三级部门-2-1-2"
}

执行后数据的结果如下，我们可以看到tree_path已经正常添加好了：

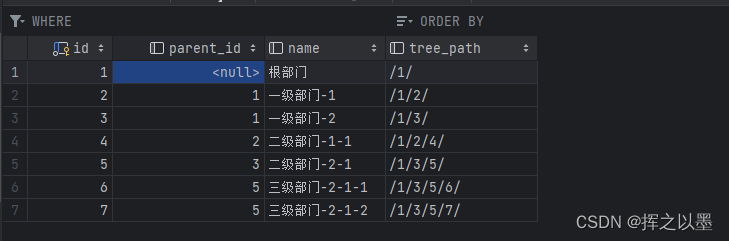
通过tree接口，不传id获取到的树结构如下，按照上面说的部门后缀进行对比验证，可以看出部门树已经正确组装了。

[{"children": [{"children": [{"children": [],"id": 4,"parentId": 2,"label": "二级部门-1-1","treePath": "/1/2/4/"}],"id": 2,"parentId": 1,"label": "一级部门-1","treePath": "/1/2/"},{"children": [{"children": [{"children": [],"id": 6,"parentId": 5,"label": "三级部门-2-1-1","treePath": "/1/3/5/6/"},{"children": [],"id": 7,"parentId": 5,"label": "三级部门-2-1-2","treePath": "/1/3/5/7/"}],"id": 5,"parentId": 3,"label": "二级部门-2-1","treePath": "/1/3/5/"}],"id": 3,"parentId": 1,"label": "一级部门-2","treePath": "/1/3/"}],"id": 1,"parentId": null,"label": "根部门","treePath": "/1/"}
]

4.2.部门修改

假设现在我想把二级部门-2-1直接挂接到根部门下，则两个三级部门也会跟着一起迁移，尝试一下做这个修改，请求参数如下：

{"id": 5,"parentId": null,"name": "二级部门-2-1（改）"
}

执行后，数据库的结果如下，tree_path中间的/3/已经去掉了：

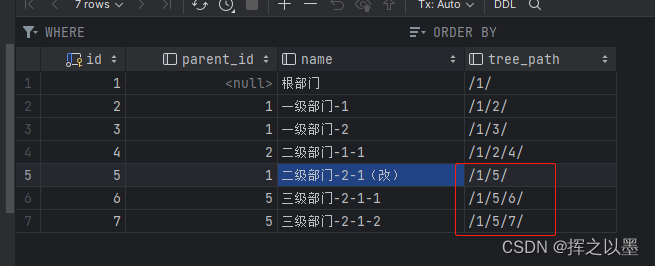
4.3.子树查询

传入二级部门-2-1（改）的id，查询子树，期望可以返回三个部门，一个父部门，两个子部门，请求tree接口的结果与期望相符：

[{"children": [{"children": [],"id": 6,"parentId": 5,"label": "三级部门-2-1-1","treePath": "/1/5/6/"},{"children": [],"id": 7,"parentId": 5,"label": "三级部门-2-1-2","treePath": "/1/5/7/"}],"id": 5,"parentId": 1,"label": "二级部门-2-1（改）","treePath": "/1/5/"}
]

5.结语

通过组合模式加上一点数据库的设计，可以实现大部分常规的树状结构的需求，希望对大家能有所帮助。