今天面试官问了我这个扔鸡蛋问题，以前学过，但是面试的时候想不起来了，应该是直接寄了，接下来总结一下这个问题的动态规划做法.

问题：有一个N层高的楼，现在给你若干个鸡蛋，要求你用最少的次数测试出第一个鸡蛋会碎的楼层

一个鸡蛋

只需要从第一层开始一层一层扔就行了，最坏情况需要扔N次

两个鸡蛋

两个鸡蛋
分析：
当我们在第i层扔鸡蛋时，会有两种情况

• 鸡蛋碎了，那代表碎了，那代表答案肯定在 [1,i-1]这个区间，鸡蛋只剩一个了，所以只能一层一层扔，所以最坏情况就是 i-1 + 1 = i次
• 鸡蛋没碎，那就又回到了对剩下的 n -i 层有两个鸡蛋测试的情况，所以此时最坏情况是 1 + dp[n-i]

所以我们需要取两种情况中次数最坏的情况

代码如下：

class Solution {
public:int twoEggDrop(int n) {if(n<=2)return n;int dp[1001];for(int i=1;i<=n;i++){int mmin=INT_MAX;for(int j=1;j<=i;j++){mmin=min(mmin,max(j,dp[i-j]+1));}dp[i]=mmin;}return dp[n];}
};

K个鸡蛋

K个鸡蛋
这里直接使用力扣网的官方题解：
动态规划法+二分查找

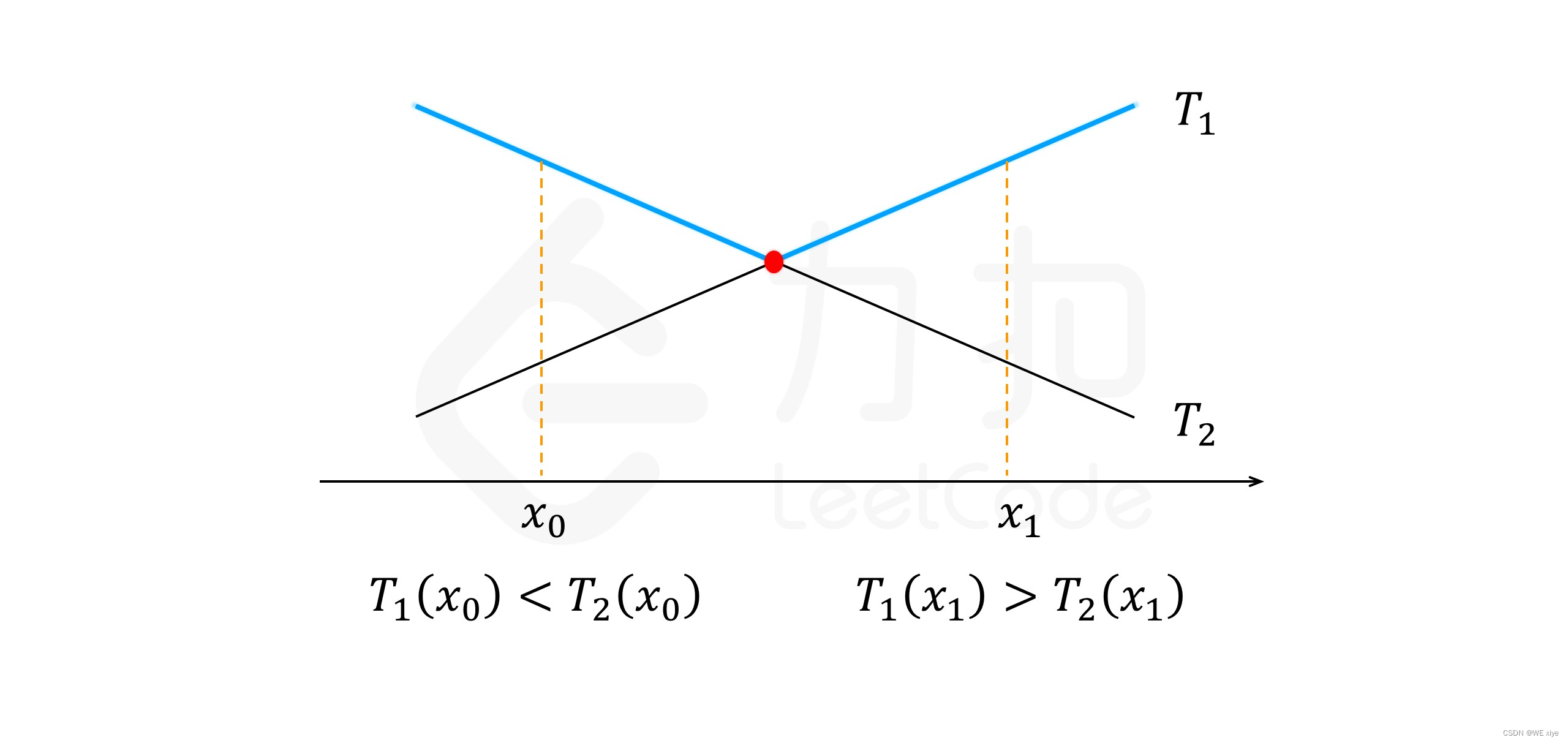
class Solution {
public:unordered_map<int,int> mmap;int dp(int k,int n){if(mmap.find(n*100+k)==mmap.end()){int ans;if(n==0)ans=0;else if(k==1)ans=n;else{int left=1;int right=n;while(left+1<right){int mid=(left+right)>>1;int t1=dp(k-1,mid-1);int t2=dp(k,n-mid);if(t1<t2){left=mid;}else if(t1>t2){right=mid;}else{left=right=mid;}}ans=1+min(max(dp(k-1,left-1),dp(k,n-left)),max(dp(k-1,right-1),dp(k,n-right)));}mmap[100*n+k]=ans;}return mmap[100*n+k];}int superEggDrop(int k, int n) {return dp(k,n);}
};