作为一门以数据及其模型为 研究对象的学科，优化模型、分析模型性能等都需要数学手段的帮助。和其他学科一样，数学 可以帮我们更清晰地描述和理解机器学习算法，也可以从理论上证明算法的有效性，是机器学习中必不可少的一环。

1 向量

向量 (vector)在数学中指具有大小和方向的量。与向量相对的，只具有大小、不具有方 向的量则称为标量 (scalar) 。 简单来说，我们可以将向量理解为由n 个数构成的n 元组， n 称 为向量的维数。向量通常有两种写法，如下所示的竖排写法称为列向量：

横排写法x=(x₁,x₂,…,x,) 称为行向量。 一个向量如果不加说明即默认为列向量，但实际中 为了节省空间，我们通常将列向量写成x=(x₁,x₂,…,x,) 的形式，其中，上标T表示转置 (transpose), 即将行和列翻转过来。行向量转置后就变成了列向量。例如，向量x=(1,2) 的

转置为

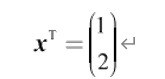
关于向量的含义，我们既可以将其看成n 维空间中的一个点，其中每一维的值代表坐标； 也可以将其看成从原点指向该坐标点的有向线段，具有长度和方向。无论哪种理解，每个 n 维 向量都与一个n 维空间中的点相对应，因此，全体n 维向量构成的空间与R"是等价的。在没有 额外说明的情况下，对于向量x∈R”, 我们用x;(1≤i≤n) 来表示其第i维的分量。此外，记 所有分量全部为0的向量为零向量0=(0,0, …,0)"。

希望尽可能找到某种形式的凸函数作为优化问题的目标。

5 小结

本章主要介绍了本书所讲解的机器学习算法中常用的数学工具。我们希望尽可能将重点放 在机器学习算法的讲解与实践上，所以并没有像数学教材那样过多地展示数学证明与定理。因 此，本章的内容以概念和定义为主，力求将这些数学概念以直观的方式展示给读者。对这些概 念的更多性质和原理感兴趣的读者，可以自行查阅相关的数学资料。

本文摘自：《动手学机器学习》

本书系统介绍了机器学习的基本内容及其代码实现，是一本着眼于机器学习教学实践的图书。

本书包含4个部分：第一部分为机器学习基础，介绍了机器学习的概念、数学基础、思想方法和最 简单的机器学习算法；第二部分为参数化模型，讲解线性模型、神经网络等算法；第三部分为非参数化 模型，主要讨论支持向量机和决策树模型及其变种；第四部分为无监督模型，涉及聚类、降维、概率图 模型等多个方面。本书将机器学习理论和实践相结合，以大量示例和代码带领读者走进机器学习的世界， 让读者对机器学习的研究内容、基本原理有基本认识，为后续进一步涉足深度学习打下基础。

本书适合对机器学习感兴趣的专业技术人员和研究人员阅读，同时适合作为人工智能相关专业机器 学习课程的教材。