目录
〇,背景
一,公开游戏、策梅洛定理
1,公开游戏
2,策梅洛定理
二,有向图游戏
1,狭义有向图游戏
2,广义有向图游戏
3,狭义有向图游戏的SG数
4,Bash Game
力扣 292. Nim 游戏(正向Bash)
51Nod 1066 Bash游戏(正向Bash)
51Nod 1067 Bash游戏 V2(正向拓展Bash)
51Nod 1068 Bash游戏 V3(正向拓展Bash)
三,公平游戏、公平组合游戏、Sprague-Grundy定理
1,公平游戏
2,公平组合游戏
3,Sprague-Grundy定理
4,Nim Game
HDU 2176 取(m堆)石子游戏 (正向Nim)
POJ 1704 Georgia and Bob (正向Nim的变形)
FZU 1928 硬币翻转游戏(正向1.5维Nim)
HDU 1907 John (反向Nim)
力扣 1908. Nim 游戏 II
5,Green Hackenbush
力扣 2005. 斐波那契树的移除子树游戏
四,有向有环图游戏
力扣 913. 猫和老鼠
〇,背景
本文收录基于有向图的博弈,提供通用的解法。
本文涉及5种博弈类型:公开游戏、有向图游戏、有向有环图游戏、公平游戏、公平组合游戏。
五者的关系:公开游戏包括有向图游戏,有向图游戏包括公平游戏,公平游戏包括公平组合游戏,而有向有环图游戏是单独的。
其中有向图游戏指的是基于有向无环图的游戏,有向有环图游戏是基于可能有环的有向图的游戏。
PS:在有向无环图上,我们定义只有胜负的游戏,而在可能有环的有向图上,我们定义有胜负平三种结局的游戏。
一,公开游戏、策梅洛定理
1,公开游戏
若一个游戏满足如下条件:
- 双人、回合制;
- 信息完全公开(perfect information);
- 无随机因素(deterministic);
- 必然在有限步内结束;
- 没有平局;
则称之为公开游戏。
2,策梅洛定理
策梅洛定理:公开游戏中的任何一个状态,要么先手有必胜策略,要么后手有必胜策略(下文把这两种状态分别称为“胜态”、“败态”)。
常见的牌类游戏大多不满足条件2、3。
常见的棋类游戏(如井字棋、五子棋、围棋、象棋、跳棋)大多满足条件2、3,在正式竞技中也会通过禁止循环的方式保证条件4,但不一定满足条件5。
二,有向图游戏
1,狭义有向图游戏
在一张有向无环图中,某一个节点上有一颗棋子,两名玩家轮流将棋子沿有向边移动,最先不能移动的一方输。

这里的绿色节点是败态,粉红色是胜态,整个图可以分为4层:

自底向上推导:
底层是最右边的最0层,是败态。
有一条边指向任意败态节点的就是胜态节点,所以第1层的2个节点是胜态。
所有边都指向胜态节点的节点的就是败态节点,所以第2层的1个节点是败态。
第3层的1个节点是胜态。
这个分层推导的例子,可以推广到所有的有向无环图,最终每个节点都有一个非负层数,层数的奇偶性直接决定是胜态还是败态。
2,广义有向图游戏
(1)推广1
在狭义有向图游戏的基础上进行推广,对于任意有向有环图,定义其中一些节点为胜或者负,两名玩家轮流将棋子沿有向边移动。
要想保证最终一定会走到定义了胜负的节点,需要保证出度为0的点一定定义了胜负,出度不为0的每一个点都可以定义或不定义胜负。
这一类游戏全部可以转化成狭义有向图游戏,具体方法是2步:
第1步,把所有定义了胜负的节点,出度置为0,即从他们出发的有向边全部删除。
第2步,新增1个定义为负的节点X,把所有定义成胜的节点,出度置为1,即从他们连一条有向边到X。
这样就转化成了狭义有向图游戏。
(2)推广2
因为有向图本身就是个建模工具,能表达丰富的信息,所以很多博弈都可以转化成有向图游戏(转化成狭义有向图游戏,或有向图游戏推广1),我们把这些游戏都称为广义有向图游戏。
一般说有向图游戏,指的都是广义有向图游戏,属于公开游戏的一种。
公开游戏可能不是广义有向图游戏,因为公开游戏可以不满足每步的走法数有限。
3,狭义有向图游戏的SG数
SG数的定义:
其中x->y表示存在x指向y的一条边,mex(S)表示不在集合S中的最小自然数。

SG为0则是败态,SG>0则是胜态。
无论是分层的方式,还是SG数,都可以通过遍历来求出所有状态是胜态还是负态。
4,Bash Game
有一堆石子共有N个。A B两个人轮流拿,A先拿。每次最少拿1颗,最多拿K颗。
正向:谁拿完就判胜,规律是N是K+1的倍数时先手负,否则先手胜
反向:谁拿完就判负,规律是N-1是K+1的倍数时先手负,否则先手胜
力扣 292. Nim 游戏(正向Bash)
题目:
你和你的朋友,两个人一起玩 Nim 游戏:桌子上有一堆石头,每次你们轮流拿掉 1 - 3 块石头。 拿掉最后一块石头的人就是获胜者。你作为先手。
你们是聪明人,每一步都是最优解。 编写一个函数,来判断你是否可以在给定石头数量的情况下赢得游戏。
示例:
输入: 4
输出: false
解释: 如果堆中有 4 块石头,那么你永远不会赢得比赛;
因为无论你拿走 1 块、2 块 还是 3 块石头,最后一块石头总是会被你的朋友拿走。
这分明是Bash Game,不是Nim Game
代码:
class Solution {
public:bool canWinNim(int n) {return n%4;}
};51Nod 1066 Bash游戏(正向Bash)
有一堆石子共有N个。A B两个人轮流拿,A先拿。每次最少拿1颗,最多拿K颗,拿到最后1颗石子的人获胜。假设A B都非常聪明,拿石子的过程中不会出现失误。给出N和K,问最后谁能赢得比赛。
例如N = 3,K = 2。无论A如何拿,B都可以拿到最后1颗石子。
Input
第1行:一个数T,表示后面用作输入测试的数的数量。(1 <= T <= 10000) 第2 - T + 1行:每行2个数N,K。中间用空格分隔。(1 <= N,K <= 10^9)
Output
共T行,如果A获胜输出A,如果B获胜输出B。
Sample Input
4
3 2
4 2
7 3
8 3Sample Output
B
A
A
B#include<iostream>
using namespace std;int main()
{int a,b;cin >> a;while (cin >> a >> b) {if (a % ++b)cout << "A\n";else cout << "B\n";}return 0;
}
51Nod 1067 Bash游戏 V2(正向拓展Bash)
有一堆石子共有N个。A B两个人轮流拿,A先拿。每次只能拿1,3,4颗,拿到最后1颗石子的人获胜。假设A B都非常聪明,拿石子的过程中不会出现失误。给出N,问最后谁能赢得比赛。
例如N = 2。A只能拿1颗,所以B可以拿到最后1颗石子。
Input
第1行:一个数T,表示后面用作输入测试的数的数量。(1 <= T <= 10000) 第2 - T + 1行:每行1个数N。(1 <= N <= 10^9)
Output
共T行,如果A获胜输出A,如果B获胜输出B。
Sample Input
3
2
3
4Sample Output
B
A
A思路:以7为周期
#include<iostream>
using namespace std;int main()
{int a;cin >> a;while (cin >> a) {if (a % 7 == 0 || a % 7 == 2)cout << "B\n";else cout << "A\n";}return 0;
}
51Nod 1068 Bash游戏 V3(正向拓展Bash)
有一堆石子共有N个。A B两个人轮流拿,A先拿。每次拿的数量只能是2的正整数次幂,比如(1,2,4,8,16....),拿到最后1颗石子的人获胜。假设A B都非常聪明,拿石子的过程中不会出现失误。给出N,问最后谁能赢得比赛。
例如N = 3。A只能拿1颗或2颗,所以B可以拿到最后1颗石子。(输入的N可能为大数)
Input
第1行:一个数T,表示后面用作输入测试的数的数量。(1 <= T <= 1000) 第2 - T + 1行:每行1个数N。(1 <= N <= 10^1000)
Output
共T行,如果A获胜输出A,如果B获胜输出B。
Sample Input
3
2
3
4Sample Output
A
B
A思路:2的幂其实就是mod 3等于1或2,所以只需要看总数是不是3的倍数
#include<iostream>
using namespace std;int main()
{int a;cin >> a;string s;while (a--) {cin >> s;int k = 0;for (int i = 0; i < s.length(); i++)k += s[i];if (k % 3 == 0)cout << "B\n";else cout << "A\n";}return 0;
}
三,公平游戏、公平组合游戏、Sprague-Grundy定理
1,公平游戏
若一个游戏满足以下条件:
1. 双人、回合制;
2. 信息完全公开(perfect information);
3. 无随机因素(deterministic);
4. 必然在有限步内结束,且每步的走法数有限(finite);
5. 没有平局;
6. 双方可采取的行动及胜利目标都相同(impartial);
7. 这个胜利目标是自己亲手达成终局状态,或者说走最后一步者为胜(normal play);
则称之为公平游戏。
公平游戏都属于有向图游戏。
虽然有向图游戏中的胜负很明确,但是如果图非常大,则遍历需要的时间很长。
2,公平组合游戏
如果一个公平游戏的每个状态,都可以表示成若干个子状态的组合,且游戏每一次操作,都只能对一个子状态进行操作,则称之为公平组合游戏。
公平组合游戏都属于公平游戏。
公平游戏可以表示成有向图,而公平组合游戏可以表示成若干个有向连通分量。
3,Sprague-Grundy定理
公平组合游戏中,一个状态的SG数,是所有子状态的SG数的异或和。
PS:只要学过NIM博弈,就很好理解了,每个公平组合游戏都可以映射成一个NIM博弈,其中每个有向连通分量,就是NIM博弈中的一个石头堆,整个有向图就是NIM博弈中的所有石头堆。
4,Nim Game
Nim is a mathematical game of strategy in which two players take turns removing (or "nimming") objects from distinct heaps or piles. On each turn, a player must remove at least one object, and may remove any number of objects provided they all come from the same heap or pile. Depending on the version being played, the goal of the game is either to avoid taking the last object or to take the last object.
正向Nim游戏就是谁拿完最后一堆获胜,规律很简单,只要保持自己每次拿完之后,所有堆的数量异或和为0 即可。
即:异或和为0时先手负,不为0时先手胜
反向是谁拿完就判负,规律比较复杂:如果至少有一堆数量大于1,那么,异或和为0时先手负,不为0时先手胜,否则,异或和为0时先手胜,不为0时先手负。
Nim游戏的SG数:一堆石头的SG数就是石头数。
HDU 2176 取(m堆)石子游戏 (正向Nim)
题目:
Description
m堆石子,两人轮流取.只能在1堆中取.取完者胜.先取者负输出No.先取者胜输出Yes,然后输出怎样取子.例如5堆 5,7,8,9,10先取者胜,先取者第1次取时可以从有8个的那一堆取走7个剩下1个,也可以从有9个的中那一堆取走9个剩下0个,也可以从有10个的中那一堆取走7个剩下3个.
Input
输入有多组.每组第1行是m,m<=200000. 后面m个非零正整数.m=0退出.
Output
先取者负输出No.先取者胜输出Yes,然后输出先取者第1次取子的所有方法.如果从有a个石子的堆中取若干个后剩下b个后会胜就输出a b.参看Sample Output.
Sample Input
2
45 45
3
3 6 9
5
5 7 8 9 10
0
Sample Output
No
Yes
9 5
Yes
8 1
9 0
10 3
Nim游戏早就被研究透了,我就不扯了,直接说结论。
取r为所有数的异或总值,如果r为0那么先手败,否则先手胜。
如果先手胜的话,他的策略是调整1个数,使得所有数的异或总值为0
也就是说,取某个x,将x变成x^r
只要x大于x^r,这个操作就是允许的。
这样的x,至少存在一个,可能会有很多个,本题要我们全部输出。
代码:
#include<iostream>
using namespace std;int num[200005];int main()
{ int m, r;while (scanf("%d",&m)){if (m == 0)break;r = 0;for (int i = 0; i < m; i++){scanf("%d", &num[i]);r = r^num[i];}if (r == 0)printf("No\n");else{printf("Yes\n");for (int i = 0; i < m; i++)if (num[i] >(num[i] ^ r))printf("%d %d\n", num[i], num[i] ^ r);}}return 0;
}POJ 1704 Georgia and Bob (正向Nim的变形)
题目:
Georgia and Bob decide to play a self-invented game. They draw a row of grids on paper, number the grids from left to right by 1, 2, 3, ..., and place N chessmen on different grids, as shown in the following figure for example:
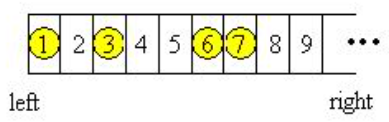
Georgia and Bob move the chessmen in turn. Every time a player will choose a chessman, and move it to the left without going over any other chessmen or across the left edge. The player can freely choose number of steps the chessman moves, with the constraint that the chessman must be moved at least ONE step and one grid can at most contains ONE single chessman. The player who cannot make a move loses the game.
Georgia always plays first since "Lady first". Suppose that Georgia and Bob both do their best in the game, i.e., if one of them knows a way to win the game, he or she will be able to carry it out.
Given the initial positions of the n chessmen, can you predict who will finally win the game?
Input
The first line of the input contains a single integer T (1 <= T <= 20), the number of test cases. Then T cases follow. Each test case contains two lines. The first line consists of one integer N (1 <= N <= 1000), indicating the number of chessmen. The second line contains N different integers P1, P2 ... Pn (1 <= Pi <= 10000), which are the initial positions of the n chessmen.
Output
For each test case, prints a single line, "Georgia will win", if Georgia will win the game; "Bob will win", if Bob will win the game; otherwise 'Not sure'.
Sample Input
2
3
1 2 3
8
1 5 6 7 9 12 14 17
Sample Output
Bob will win
Georgia will win
题意:
有N个棋子排成一排,位置分别是所给定的整数,双方轮流把其中一个棋子往左移,但是不能超过左边的棋子,也不能移到同一个位置,只能移到它的右边一格。
问先手还是后手有必胜策略。
思路:
两两一组,如果是奇数个,最左边的单独一组,通过差分,化成Nim博弈
代码:
#include<iostream>
#include<algorithm>
using namespace std;int main()
{int T, n, s, l[1005];cin >> T;while (T--){cin >> n;s = 0;for (int i = 0; i < n; i++)cin >> l[i];sort(l, l + n);if (n % 2)s = l[0] - 1;for (int i = n % 2; i < n; i += 2)s ^= l[i + 1] - l[i] - 1;if (s)cout << "Georgia will win\n";else cout << "Bob will win\n";}return 0;
}FZU 1928 硬币翻转游戏(正向1.5维Nim)
题目:
Description
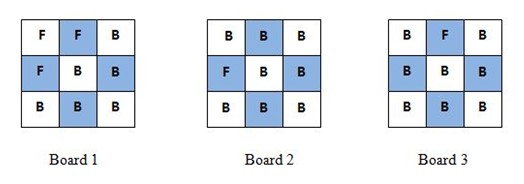
Alice和Bob决定玩一种硬币翻转游戏。游戏的最初有n * m个硬币被放在一个棋盘上,有的正面朝上,有的反面朝上,当游戏开始的时候,他们轮流对硬币进行操作。
游戏的规则是这样的,当轮到一个人操作的时候,他必须挑选两枚硬币,将它们分别翻转(不是交换),同时这两枚硬币必须满足以下条件:
1. 两枚硬币必须在同一行或同一列
2. 两枚硬币中最右下的那枚必须是从正面翻转到反面
当一方无法做出满足上面要求的操作时,这一方就输了,游戏结束。
比如,当游戏初始状态是棋盘1时,Alice翻转完2枚硬币,可以将其变成 棋盘2的状态或棋盘3的状态。
Alice总是第一个操作,假设Alice和Bob都采取最优策略来玩这个游戏,请 你写一个程序判断Alice是否能赢。
Input
首先第一行为T,表示有T组数据。接下来为每组数据的结构:
每组测试数据的第一行有两个整数n和m (2 <= n, m <= 1000),代表棋盘上排列着n行m列的硬币,接下来n行,每行 m个字符描述硬币的初始状态,’F’代表硬币正面朝上,’B’代表硬币反面朝上。
Output
对于每组数据输出一行先输出组数(从1开始),接下来如果Alice能赢,输出YES,否则输出NO.
Sample Input
2
2 2
FB
BB
2 2
BF
BB
Sample Output
Case 1: NO
Case 2: YES
我只能说这个OJ绝对有毒啊
#include<iostream>
using namespace std;int main()
{int t, n, m, ans = 0;cin >> t;char c;for (int cas = 1; cas <= t; cas++){cin >> n >> m;for (int i = 0; i < n; i++)for (int j = 0; j < m; j++){cin >> c;if (c == 'F')ans ^= (i^j);}if (ans)cout << "Case " << cas << ": " << "YES" << endl;else cout << "Case " << cas << ": " << "NO" << endl;}return 0;
}HDU 1907 John (反向Nim)
Little John is playing very funny game with his younger brother. There is one big box filled with M&Ms of different colors. At first John has to eat several M&Ms of the same color. Then his opponent has to make a turn. And so on. Please note that each player has to eat at least one M&M during his turn. If John (or his brother) will eat the last M&M from the box he will be considered as a looser and he will have to buy a new candy box.
Both of players are using optimal game strategy. John starts first always. You will be given information about M&Ms and your task is to determine a winner of such a beautiful game.
Input
The first line of input will contain a single integer T – the number of test cases. Next T pairs of lines will describe tests in a following format. The first line of each test will contain an integer N – the amount of different M&M colors in a box. Next line will contain N integers Ai, separated by spaces – amount of M&Ms of i-th color.
Constraints:
1 <= T <= 474,
1 <= N <= 47,
1 <= Ai <= 4747
Output
Output T lines each of them containing information about game winner. Print “John” if John will win the game or “Brother” in other case.
Sample Input
2
3
3 5 1
1
1Sample Output
John
Brother思路:
flag表示至少有1堆的数量大于1,s表示异或和,那么if (flag ^ (s > 0))则后手胜,否则先手胜。
代码:
#include<iostream>
using namespace std;int main()
{int n, a[50];cin >> n;while (cin >> n) {int flag = 0, s = 0;for (int i = 0; i < n; i++) {cin >> a[i];if (a[i] > 1)flag = 1;s ^= a[i];}if (flag ^ (s > 0))cout << "Brother\n";else cout << "John\n";}return 0;
}
力扣 1908. Nim 游戏 II
Alice 和 Bob 交替进行一个游戏,由 Alice 先手。
在游戏中,共有 n 堆石头。在每个玩家的回合中,玩家需要 选择 任一非空石头堆,从中移除任意 非零 数量的石头。如果不能移除任意的石头,就输掉游戏,同时另一人获胜。
给定一个整数数组 piles ,piles[i] 为 第 i 堆石头的数量,如果 Alice 能获胜返回 true ,反之返回 false 。
Alice 和 Bob 都会采取 最优策略 。
示例 1:
输入:piles = [1]
输出:true
解释:只有一种可能的情况:
- 第一回合,Alice 移除了第 1 堆中 1 块石头。piles = [0]。
- 第二回合,Bob 没有任何石头可以移除。Alice 获胜。
示例 2:
输入:piles = [1,1]
输出:false
解释:可以证明,Bob一定能获胜。一种可能的情况:
- 第一回合,Alice 移除了第 1 堆中 1 块石头。 piles = [0,1]。
- 第二回合,Bob 移除了第 2 堆中 1 块石头。 piles = [0,0]。
- 第三回合,Alice 没有任何石头可以移除。Bob 获胜。
示例 3:
输入:piles = [1,2,3]
输出:false
解释:可以证明,Bob一定能获胜。一种可能的情况:
- 第一回合,Alice 移除了第 3 堆中 3 块石头。 piles = [1,2,0]。
- 第二回合,Bob 移除了第 2 堆中 1 块石头。 piles = [1,1,0]。
- 第三回合,Alice 移除了第 1 堆中 1 块石头。piles = [0,1,0]。
- 第四回合,Bob 移除了第 2 堆中 1 块石头。 piles = [0,0,0]。
- 第三回合,Alice 没有任何石头可以移除。Bob 获胜。
提示:
n == piles.length
1 <= n <= 7
1 <= piles[i] <= 7
进阶:你能想出一个 线性时间 的解决方案吗?虽然这一答案可能超出了面试所需的范围,但了解它可能会很有趣。
class Solution {
public:bool nimGame(vector<int>& piles) {int ans=0;for(auto x:piles)ans^=x;return ans;}
};5,Green Hackenbush
Hackenbush游戏是通过移除一个有根图的某些边并自动不和根相连的部分,最终没有边可移除则判负。
Green Hackenbush,每条边都是绿色的,双方都可以操作。
Blue-Red Hackenbush,有些边是蓝色,有些边是红色,而玩家一只能删除蓝色边,玩家二只能删除红色边。
力扣 2005. 斐波那契树的移除子树游戏
斐波那契树是一种按这种规则函数 order(n) 创建的二叉树:
order(0)是空树。order(1)是一棵只有一个节点的二叉树。order(n)是一棵根节点的左子树为order(n - 2)、右子树为order(n - 1)的二叉树。
Alice 和 Bob 在玩一种关于斐波那契树的游戏,由 Alice 先手。在每个回合中,每个玩家选择一个节点,然后移除该节点及其子树。只能删除根节点 root 的玩家输掉这场游戏。
给定一个整数 n,假定两名玩家都按最优策略进行游戏,若 Alice 赢得这场游戏,返回 true 。若 Bob 赢得这场游戏,返回 false 。
一棵二叉树的子树 tree 是由 tree 中某个节点及其所有后代节点组成的树。树 tree 也可当作自身的子树。
示例 1:

输入: n = 3 输出: true 解释: Alice 移除右子树中的节点 1。 Bob 要么移除左子树中的 1,要么移除右子树中的 2。 Alice 可以移除 Bob 未移除的任意节点。 Bob 只能删除根节点 3,所以 Bob 输了。 返回 true,因为 Alice 赢了。
示例 2:

输入: n = 1 输出: false 解释: Alice 只能移除根节点 1, 所以 Alice 输了。 返回 false,因为 Alice 输了。
示例 3:
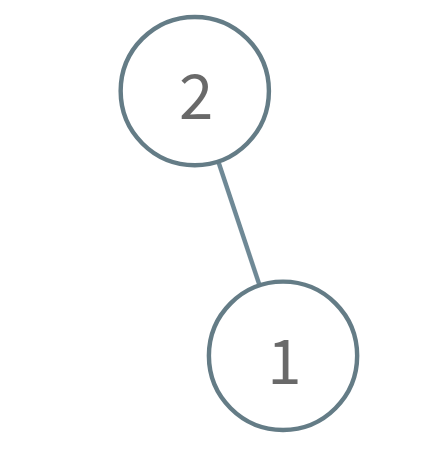
输入: n = 2 输出: true 解释: Alice 删除节点 1. Bob 只能删除根节点 2,所以 Bob 输了。 返回 true,因为 Alice 赢了。
提示:
1 <= n <= 100
思路:Green Hackenbush的一个特例。
如果是树而不是图,那么sg函数的递推式就是sg(root) = (sg(left)+1) ^ (sg(right)+1)
所以本题的sg值就是0 1 3 6 3 3 0 5 7 14 7 7 0 9 11 6 11 0 13......
class Solution {
public:bool findGameWinner(int n) {return n%6-1;}
};四,有向有环图游戏
在一张可能有环的有向图中,某一个节点上有一颗棋子,两名玩家轮流将棋子沿有向边移动,要么走到预先定义了胜负平的节点,要么沿着环移动判定为平局。
策略:
(1)能走到负节点,那就走到负节点,当前就是胜节点
(2)如果只能走到胜节点,那我就是负节点
(3)反复运用前2条规则之后,还没有确定的节点,都是平节点,包括有环的情况。
按照这个策略,其实求解过程也不难。
class SG2 {
public://输入每个节点的出度out, 反图rg,已知胜1负-1平0的节点集s,节点从0开始编号static void solve(vector<int>&out, map<int, vector<int>> &rg, map<int, int>&s){vector<int>visit(out.size());vector<int>v1, v2;for (auto si : s) {visit[si.first] = 1;if (si.second == -1)v1.push_back(si.first);if (si.second == 1)v2.push_back(si.first);}while (!v1.empty() || !v2.empty())fresh(v1, v2, s, visit, rg,out);for (int i = 0; i < out.size(); i++)s[i];}
private:static void fresh(vector<int>&v1, vector<int>&v2, map<int, int>&s, vector<int>&visit, map<int, vector<int>> &rg, vector<int>&out) {for (auto x : v1) {for (auto x2 : rg[x])if (visit[x2] == 0) {s[x2] = 1, v2.push_back(x2), visit[x2] = 1;}}v1.clear();for (auto x : v2) {for (auto x2 : rg[x])if (visit[x2] == 0) {if (--out[x2] == 0)s[x2] = -1, v1.push_back(x2), visit[x2] = 1;}}v2.clear();}
};力扣 913. 猫和老鼠
两位玩家分别扮演猫和老鼠,在一张 无向 图上进行游戏,两人轮流行动。
图的形式是:graph[a] 是一个列表,由满足 ab 是图中的一条边的所有节点 b 组成。
老鼠从节点 1 开始,第一个出发;猫从节点 2 开始,第二个出发。在节点 0 处有一个洞。
在每个玩家的行动中,他们 必须 沿着图中与所在当前位置连通的一条边移动。例如,如果老鼠在节点 1 ,那么它必须移动到 graph[1] 中的任一节点。
此外,猫无法移动到洞中(节点 0)。
然后,游戏在出现以下三种情形之一时结束:
- 如果猫和老鼠出现在同一个节点,猫获胜。
- 如果老鼠到达洞中,老鼠获胜。
- 如果某一位置重复出现(即,玩家的位置和移动顺序都与上一次行动相同),游戏平局。
给你一张图 graph ,并假设两位玩家都都以最佳状态参与游戏:
- 如果老鼠获胜,则返回
1; - 如果猫获胜,则返回
2; - 如果平局,则返回
0。
示例 1:

输入:graph = [[2,5],[3],[0,4,5],[1,4,5],[2,3],[0,2,3]] 输出:0
示例 2:
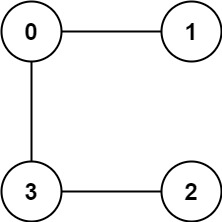
输入:graph = [[1,3],[0],[3],[0,2]] 输出:1
提示:
3 <= graph.length <= 501 <= graph[i].length < graph.length0 <= graph[i][j] < graph.lengthgraph[i][j] != igraph[i]互不相同- 猫和老鼠在游戏中总是可以移动
class Solution {
public:int catMouseGame(vector<vector<int>>& graph) {map<int, map<int, map<int, int>>>mn;map<int, int>s;int id = 0;for (int m = 0; m < graph.size(); m++) {for (int c = 0; c < graph.size(); c++) {for (int t = 0; t <= 1; t++) {mn[m][c][t] = id;if (m == 0 || c == 0)s[id] = (t ? -1 : 1);else if (m == c)s[id] = (t ? 1 : -1);id++;}}}vector<int>out(id);map<int, vector<int>> rg;for (int m = 0; m < graph.size(); m++) {for (int c = 0; c < graph.size(); c++) {for (auto m2 : graph[m])out[mn[m][c][0]]++, rg[mn[m2][c][1]].push_back(mn[m][c][0]);for (auto c2 : graph[c])out[mn[m][c][1]]++, rg[mn[m][c2][0]].push_back(mn[m][c][1]);}}SG2::solve(out, rg, s);int ans = s[mn[1][2][0]];return ans == -1 ? 2 : ans;}
};