代码随想录第46天|139.单词拆分，了解多重背包，背包总结

139.单词拆分

动规五部曲

1.确定valid数组以及下标的含义

valid[i] : 字符串长度为i的话，valid[i]为true，表示可以拆分为一个或多个在字典中出现的单词。

2.valid初始化

valid[0]一定要为true，否则递推下去后面都都是false了

3.递推公式

所以递推公式是 if([j, i] 这个区间的子串出现在字典里 && valid[j]是true) 那么 valid[i] = true。

4.遍历顺序

关于求组合还是排列还是最小数做一个总结：

求组合数：动态规划：518.零钱兑换II (opens new window)

求排列数：动态规划：377. 组合总和 Ⅳ (opens new window)，动态规划：70. 爬楼梯进阶版（完全背包） (opens new window)

求最小数：动态规划：322. 零钱兑换 (opens new window)、动态规划：279.完全平方数

而本题其实我们求的是排列数，为什么呢。拿 s = "applepenapple", wordDict = ["apple", "pen"] 举例。

"apple", "pen" 是物品，那么我们要求物品的组合一定是 "apple" + "pen" + "apple" 才能组成 "applepenapple"。

"apple" + "apple" + "pen" 或者 "pen" + "apple" + "apple" 是不可以的，那么我们就是强调物品之间顺序。

所以说，本题一定是先遍历背包，再遍历物品。

5.推导

代码实现

class Solution {public boolean wordBreak(String s, List<String> wordDict) {//完全背包//valid[i]表示字符串下标为i时，可以被字符串列表中的字符拼接出来HashSet<String> set=new HashSet<>(wordDict);//，将字典 wordDict 转化为一个 HashSet 集合 setboolean[] valid=new boolean[s.length()+1];//valid[i] 表示从字符串 s 的第 0 个字符到第 i 个字符（不包括第 i 个字符）所组成的子串是否可以被字典中的单词拆分。valid[0]=true;for(int i=1;i<=s.length();i++){for(int j=0;j<i&&!valid[i];j++){if(set.contains(s.substring(j,i))&&valid[j]){//i表示截取的结束位置，j表示截取的起始位置//对于每个子串，检查它是否存在字典中valid[i]=true;//表示从0到i的子串可以被拆分}}}return valid[s.length()];//表示整个字符串s是否可以被拆分成字典中的单词}
}

多重背包

有N种物品和一个容量为V 的背包。第i种物品最多有Mi件可用，每件耗费的空间是Ci ，价值是Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间总和不超过背包容量，且价值总和最大。

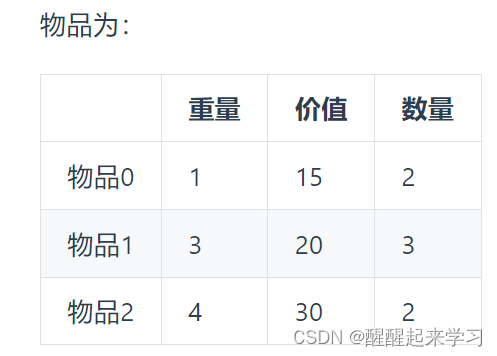
其实多重背包和01背包很想，01背包每个物品只有1个，多重背包只是每个物品有多个

ublic void testMultiPack1(){// 版本一：改变物品数量为01背包格式List<Integer> weight = new ArrayList<>(Arrays.asList(1, 3, 4));List<Integer> value = new ArrayList<>(Arrays.asList(15, 20, 30));List<Integer> nums = new ArrayList<>(Arrays.asList(2, 3, 2));int bagWeight = 10;for (int i = 0; i < nums.size(); i++) {while (nums.get(i) > 1) { // 把物品展开为iweight.add(weight.get(i));value.add(value.get(i));nums.set(i, nums.get(i) - 1);}}int[] dp = new int[bagWeight + 1];for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = bagWeight; j >= weight.get(i); j--) { // 遍历背包容量dp[j] = Math.max(dp[j], dp[j - weight.get(i)] + value.get(i));}System.out.println(Arrays.toString(dp));}
}