二分查找

  二分查找算法是一种在有序数组中查找特定元素的搜索算法。算法的工作原理是，通过比较数组中间元素和目标值，如果目标值等于中间元素，那么查找结束。如果目标值小于或大于中间元素，则在数组的前半部分或后半部分进行查找。此过程将一直持续到找到目标值，或者搜索范围为空。

  需要注意的是，二分查找算法只适用于已排序的数组。如果给定的数组是无序的，那么在进行二分查找之前，需要先对数组进行排序。

  以下是一个朴素二分查找算法的步骤：

  （1）选择数组的中间元素。

  （2）如果中间元素正好是要查找的元素，则搜索过程结束。

  （3）如果要查找的元素大于中间元素，则在数组的后半部分进行搜索。

  （4）如果要查找的元素小于中间元素，则在数组的前半部分进行搜索。

             

704. 二分查找

二分查找

（1）二分查找

  算法思路：(当 right = nums.size()-1 时)

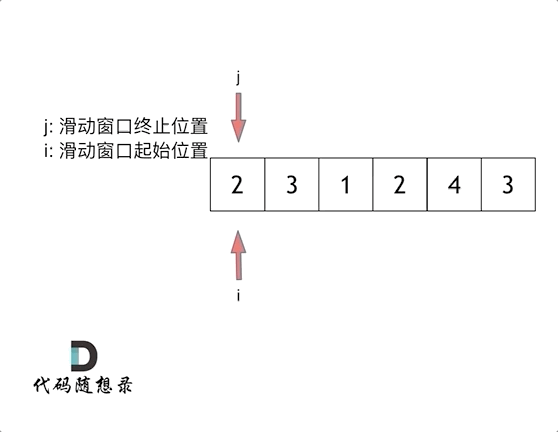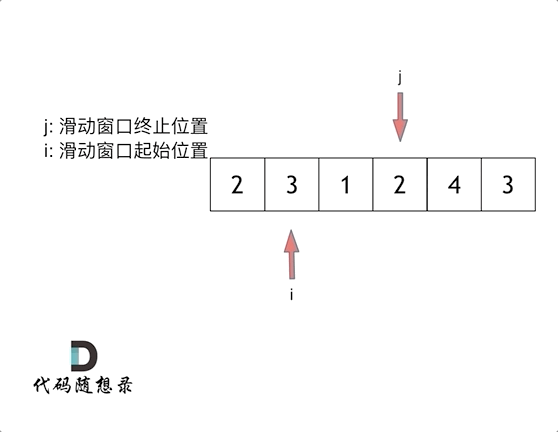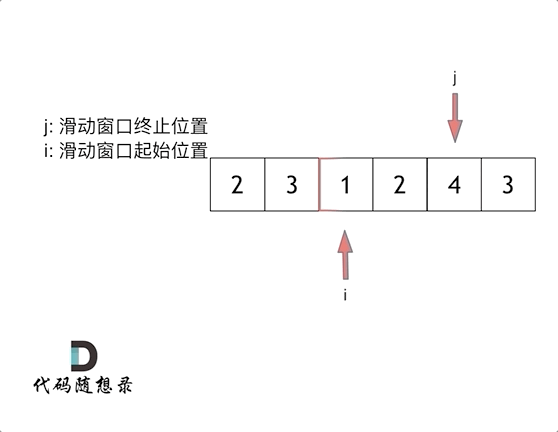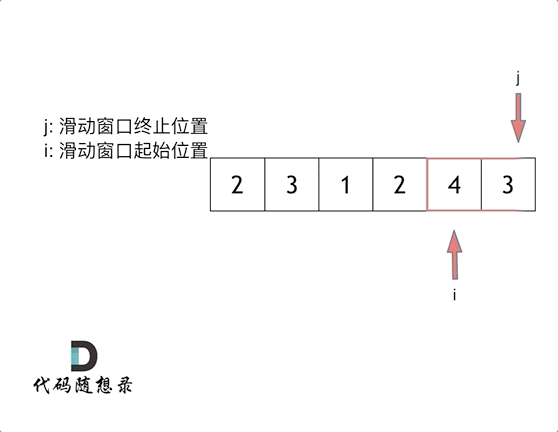
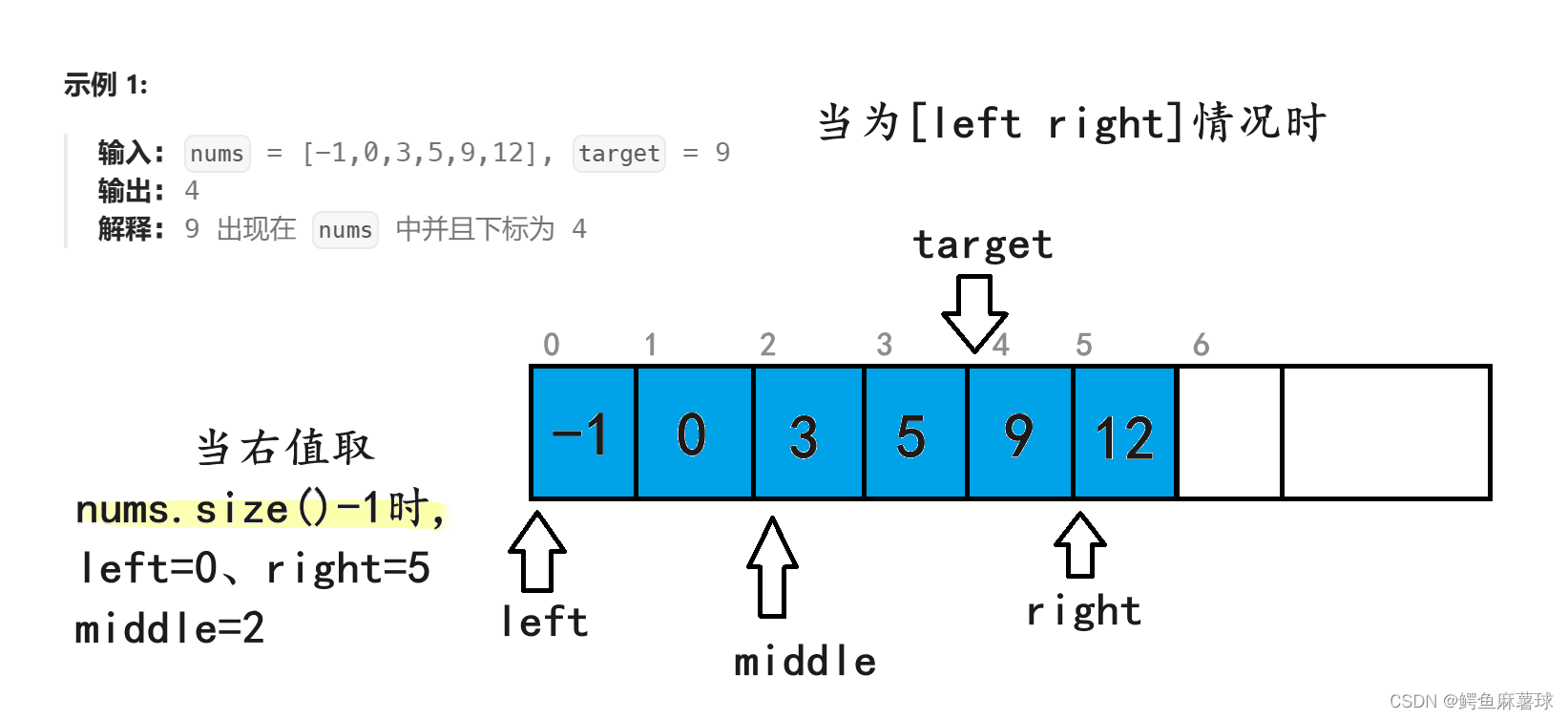
  我们定义 left ， right 指针，分别指向数组的左右区间。之后找到待查找区间的中间点 middle ，找到之后分三种情况讨论：

（1）nums[middle] == target 说明正好找到，返回 mid 的值；

（2）nums[middle] > target 说明 [middle, right] 这段区间都是大于 target 的， 因此舍去右边区间，在左边 [left, middle -1] 的区间继续查找，即让 right = middle - 1 ,然后重复 2 过程；

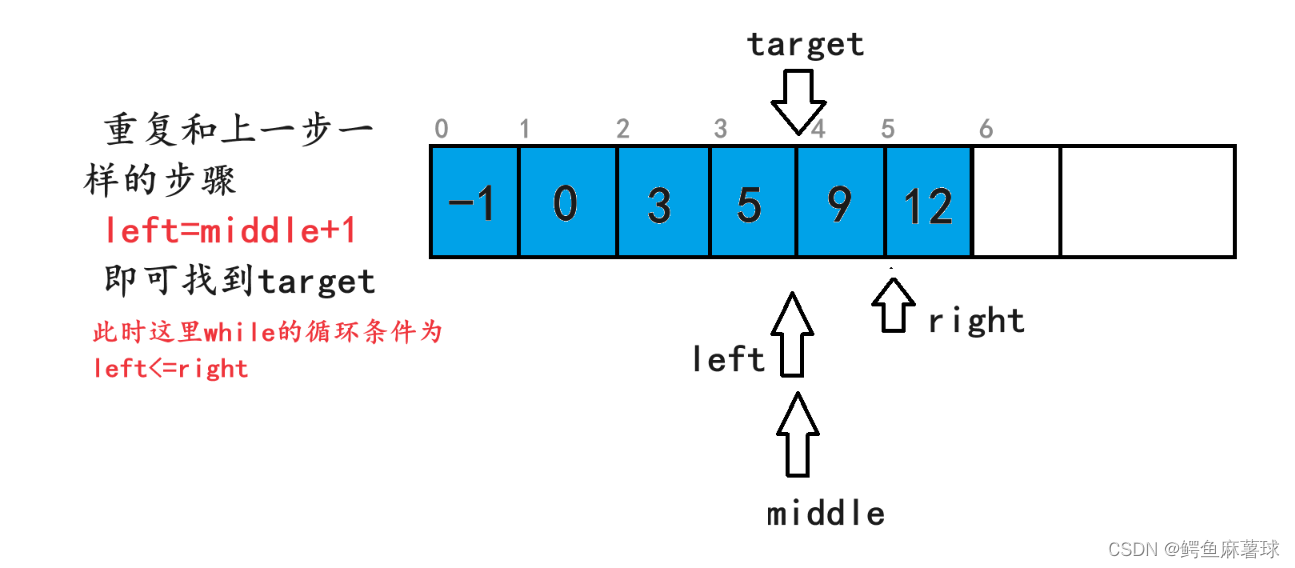
（3）nums[middle] < target 说明 [left, middle] 这段区间的值都是小于 target 的， 因此舍去左边区间，在右边 [middle + 1, right] 区间继续查找，即让 left = middle + 1 ,然后重复 2 过程；

  当 left 与 right 错开时，说明整个区间都没有这个数，返回 -1。

             

  算法实现过程：(当 right = nums.size()-1 时)

  首先，它初始化两个指针，‘left’和’right’，分别指向数组的开始和结束。 然后，它进入一个循环，在循环中，它找到数组中间的元素（‘middle’），并根据这个中间元素和目标值的比较结果来更新搜索范围。

  如果中间元素等于目标值，那么函数就返回中间元素的索引。

  如果中间元素大于目标值，那么目标值必然在数组的左半部分， 所以它将’right’指针移动到’middle - 1’，缩小搜索范围为左半部分。

  否则，目标值必然在数组的右半部分， 所以它将’left’指针移动到’middle + 1’，缩小搜索范围为右半部分。

  如果在数组中没有找到目标值，那么函数返回-1。

class Solution {
public:int search(vector<int>& nums, int target) {int left=0,right=nums.size()-1;while(left<=right)//[left right]{int middle=(right+left)/2;if(nums[middle]==target)return middle;else if(nums[middle]>target)//[left target middle   ...  right]right=middle-1;             //[left target right]else                        //[left  ...   middle target right]left=middle+1;              //[left target right]}return -1;}
};

             

当然right也可以等于nums.size()

  和上面的代码实现基本类似，只是有些条件需要改变。

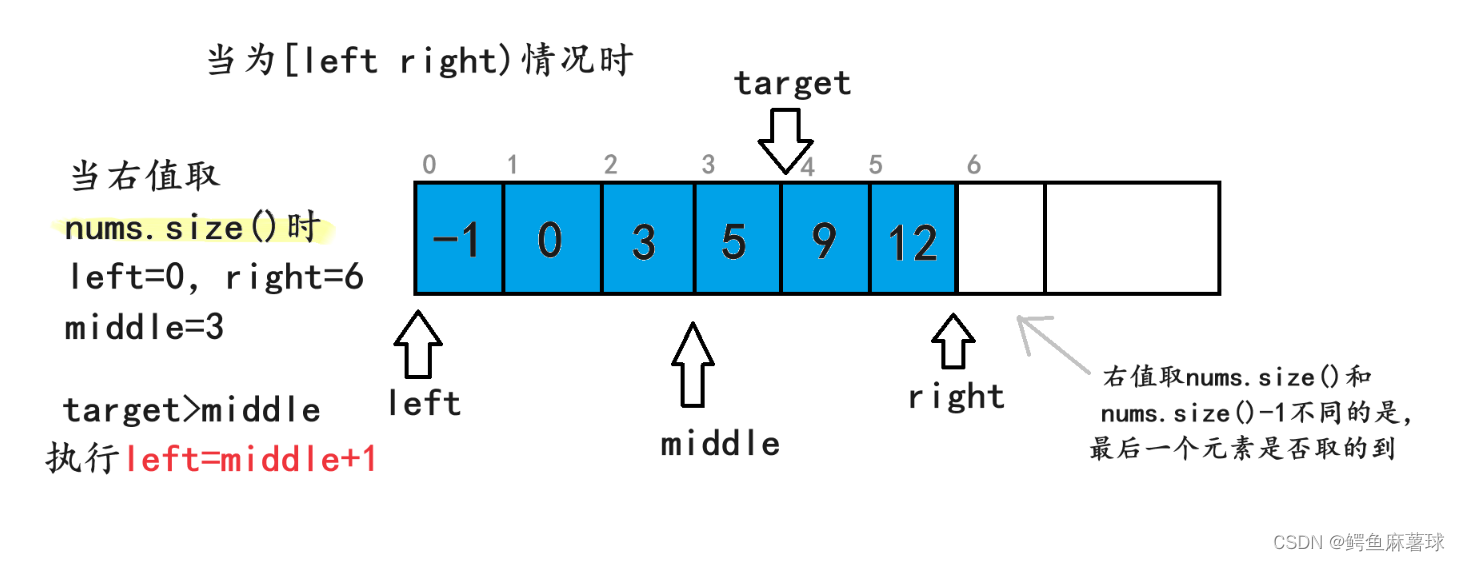
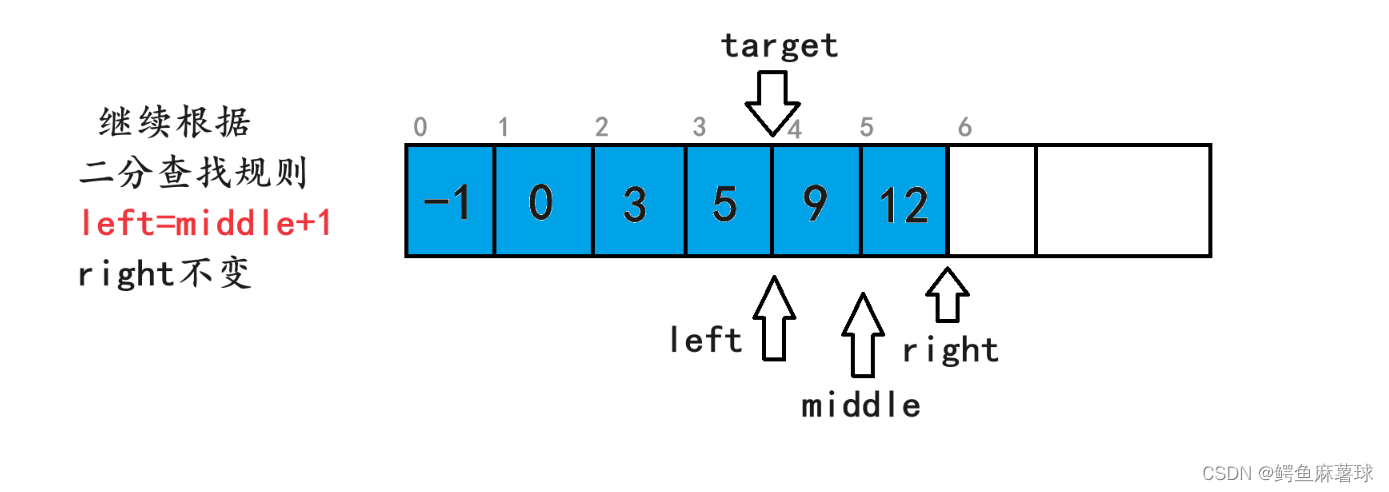
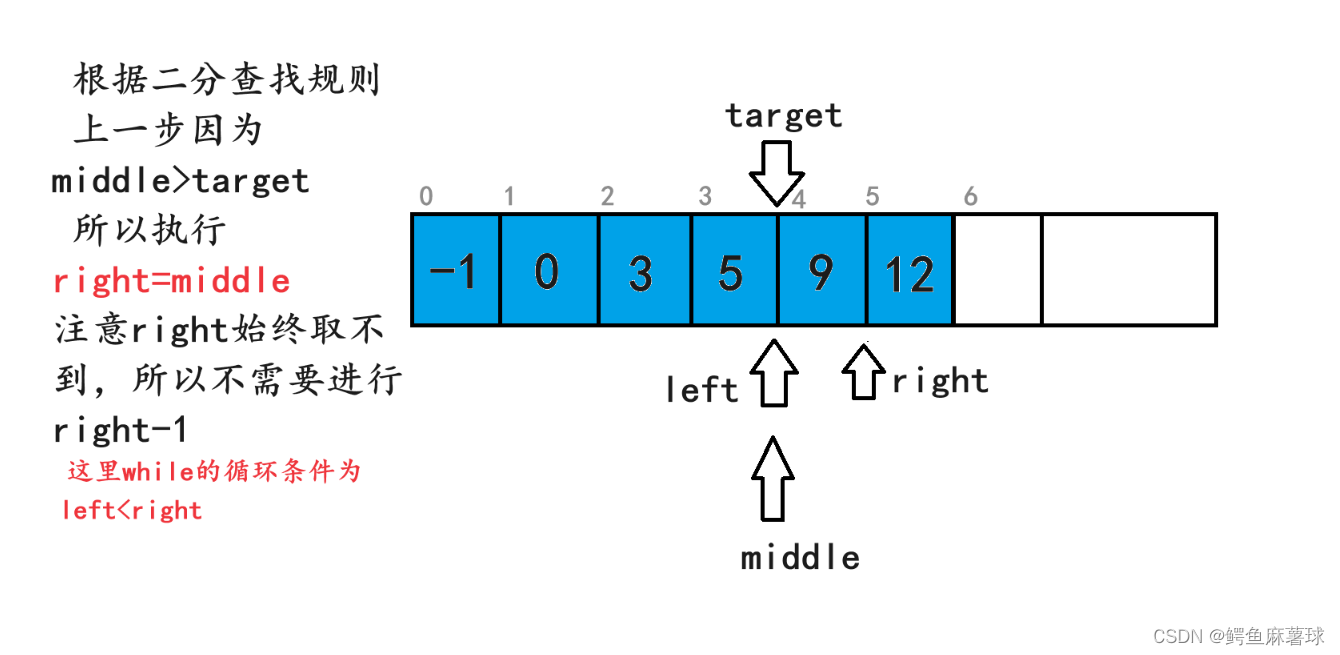
class Solution {
public:int search(vector<int>& nums, int target) {int left=0,right=nums.size();while(left<right)//[left right){int middle=(right+left)/2;if(nums[middle]==target)return middle;else if(nums[middle]>target)//[left target middle   ...  right)right=middle;               //[left target right)else                        //[left  ...   middle target right)left=middle+1;              //[left target right)}return -1;}
};

时间复杂度：O(logn)

             

35. 搜索插入位置

搜索插入位置

             

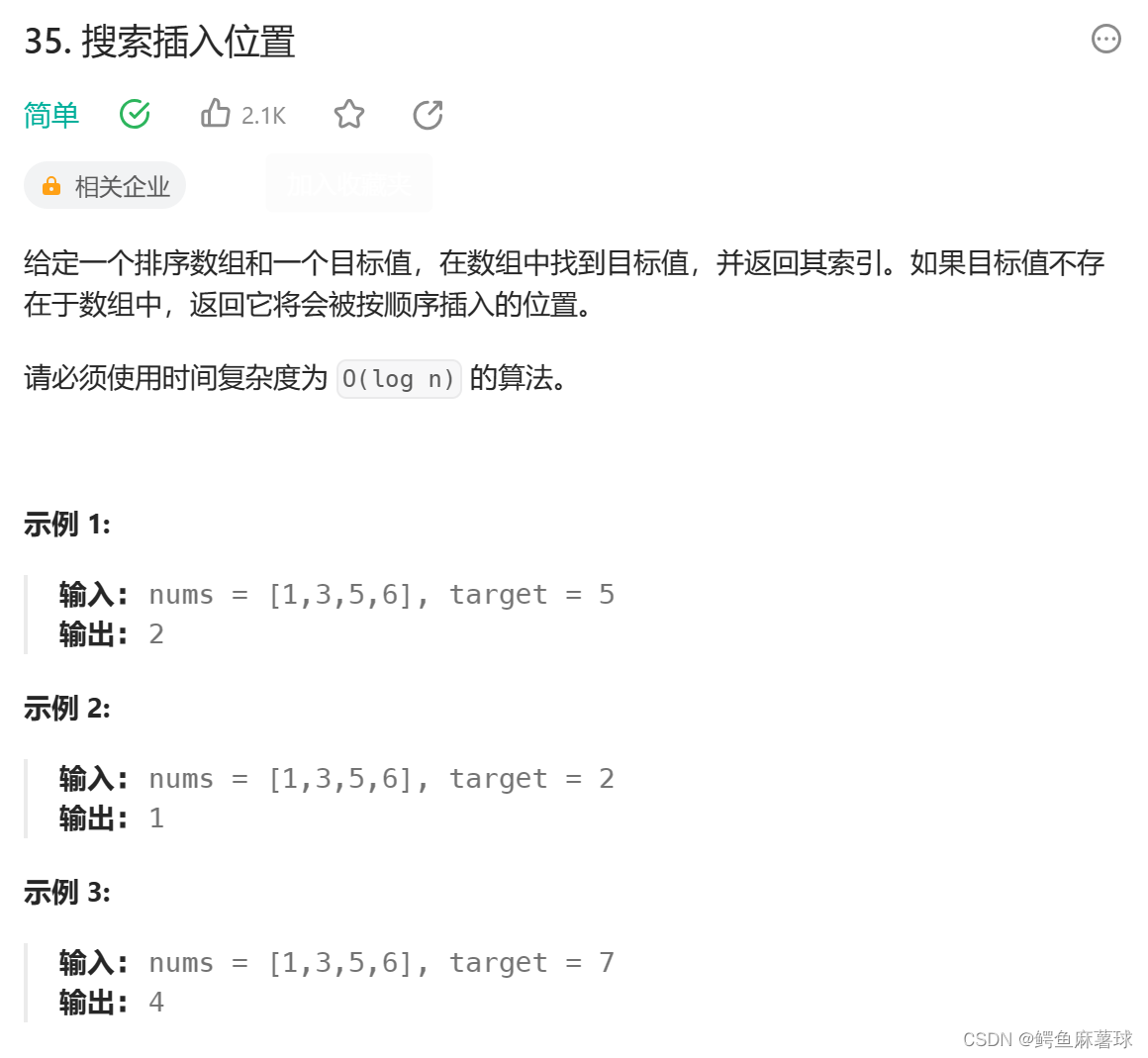
（1）二分查找

  算法思路：

  （1）设插入位置的坐标为 index ， 根据插入位置的特点可以知道：
  [left, index - 1] 内的所有元素均是小于 target 的；
  [index, right] 内的所有元素均是大于等于 target 的。

  （2）设 left 为本轮查询的左边界， right 为本轮查询的右边界。 根据 mid 位置元素的信息，分析下⼀轮查询的区间：
  当 nums[mid] >= target 时，说明 mid 落在了 [index, right] 区间上， mid 左边包括 mid 本身，可能是最终结果，所以我们接下来查找的区间在 [left, mid] 上。因此，更新 right 到 mid 位置，继续查找。
  当 nums[mid] < target 时，说明 mid 落在了 [left, index - 1] 区间上， mid 右边但不包括 mid 本⾝，可能是最终结果，所以我们接下来查找的区间在 [mid +1, right] 上。因此，更新 left 到 mid + 1 的位置，继续查找。

  （3）直到我们的查找区间的长度变为 1 ，也就是 left == right 的时候， left 或者right 所在的位置就是我们要找的结果。

             

  算法实现：

  （1）初始化两个指针，left和right，分别指向数组的开始和结束。

  （2）进入一个while循环，只要left小于right，循环就会继续。 在循环中，首先找到数组中间的元素（mid）。

  （3）如果中间元素小于目标值，那么目标值必然在数组的右半部分，所以将left移动到mid+1，缩小搜索范围为右半部分。

  （4）否则，目标值必然在数组的左半部分或者就是中间元素本身，所以将right移动到mid，缩小搜索范围为左半部分或者就是中间元素。

  （5）当循环结束时，right指向的元素可能是目标值，也可能不是。如果这个元素小于目标值，说明目标值应该插入到数组的右侧，所以返回right+1；否则，返回right。

class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left=0,right=nums.size()-1;while(left<right){int mid=(left+right)/2;if(nums[mid]<target)left=mid+1;elseright=mid;}if(nums[right]<target)//判断target是否大于nums中的最大值return right+1;return right;}
};

时间复杂度：O(logn)