你知道吗?对于连续的”构造+拷贝构造“,编译器其实是会默默做出优化的。👻
如果你不知道这个知识点的话,那下面这道笔试题就要失分了😵。
本篇分享一个关于编译器优化的小知识,看完本篇,你就能知道程序里的 构造函数、拷贝构造函数 究竟被调了几次~
题目引入
某笔试题:下面的程序经历了几次构造?几次拷贝构造?

答案为:
1次构造,4次拷贝
对此题的分析在本篇末尾。如果你对这道题尚有存疑,那相信看完本篇,你的疑惑将会烟消云散~👻
传值传参 的优化
我们知道,传值传参会产生拷贝,因为这样能保证 函数内部对参数的操作 不会影响到原始变量的值。
➡️先看一个没做优化的例子:
class W
{
public://构造函数W(int w) :_w(w){cout << "W()" << endl;}//拷贝构造函数W(const W& w) :_w(w._w){cout << "W(const W& w)" << endl;}//析构函数~W(){cout << "~W()" << endl;}
private:int _w;
};
void func(const W w) {}
int main()
{W w1=1; //构造func(w1); //拷贝构造:把w1的值拷贝一份,传到形参return 0;
}调用情况我们打印出来:

可见这种情况下:
W w1=1;
func(w1);是老老实实调用构造+拷贝构造的,并没有做出优化。
➡️再看一个做了优化的例子:
class W
{
public://构造函数W(int w) :_w(w){cout << "W()" << endl;}//拷贝构造函数W(const W& w) :_w(w._w){cout << "W(const W& w)" << endl;}//析构函数~W(){cout << "~W()" << endl;}
private:int _w;
};
void func(const W w) {}
int main()
{func(W(1)); //一个表达式步骤中,有连续的”构造+拷贝构造“return 0;
}结果:
我们发现:这次没调拷贝构造了!看来编译器做了优化。
原本,这个表达式的执行顺序是:W(1)先构造出一个W,这个W再拷贝构造,传递给形参,参与表达式func()。
func(W(1));而编译器做出了优化:
将连续的 构造+拷贝构造 优化成一步构造。
动图可以更直观地看出来:
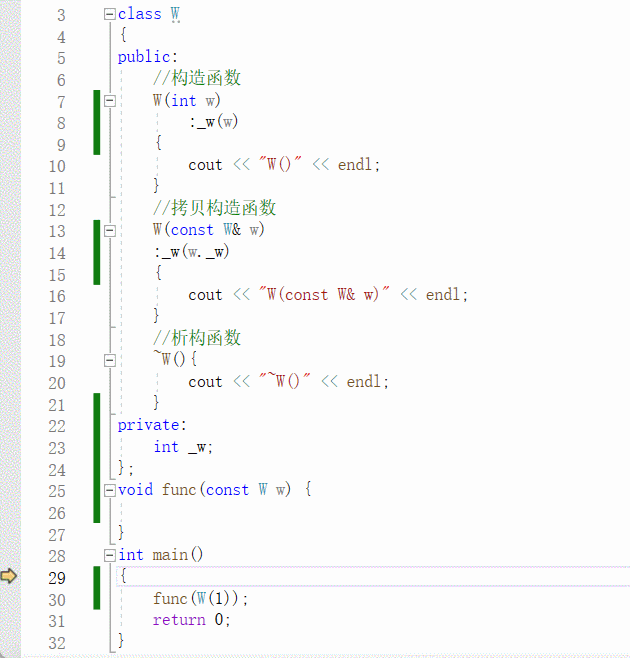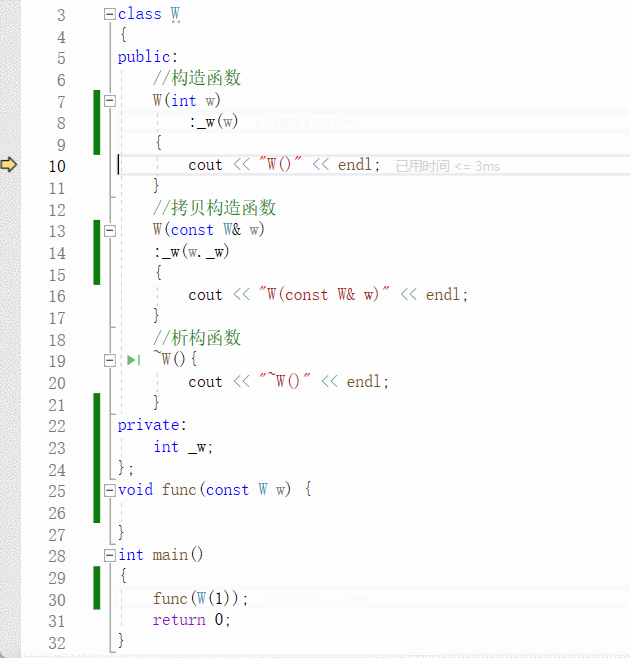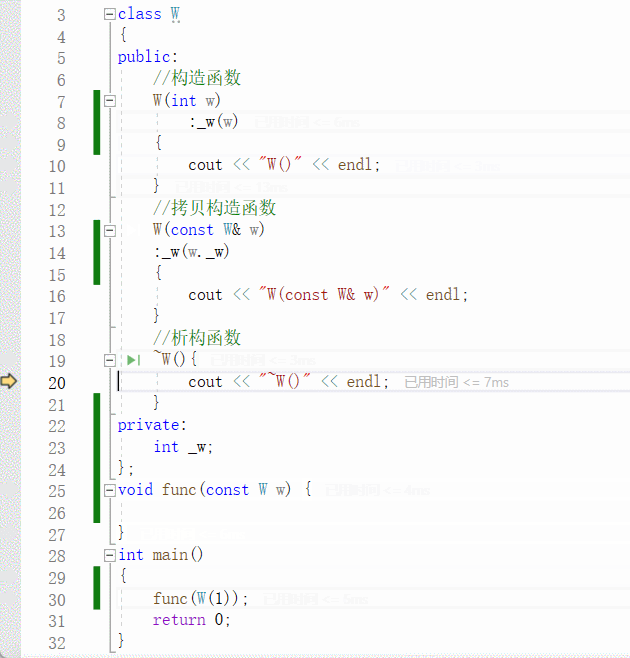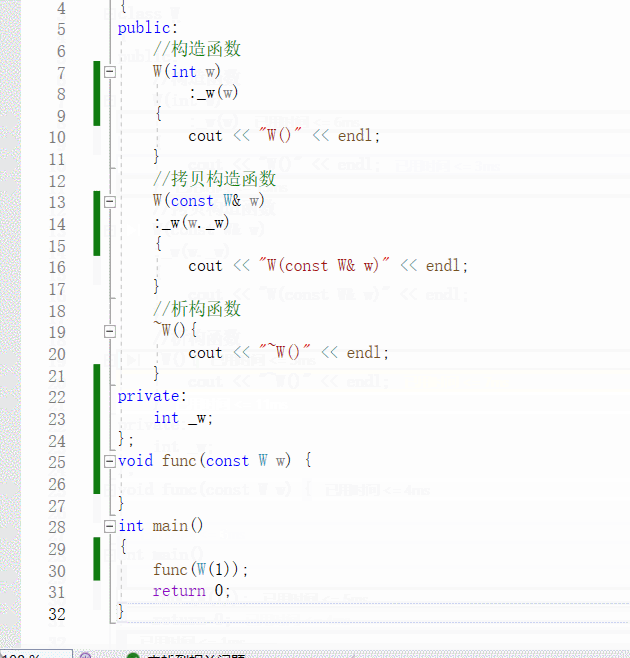
传匿名对象 的优化
我们学过的匿名对象,也是可以传参过去的,它的优化和刚刚讲的传值传参的优化 道理是一样的。
class W
{
public:W() {cout << "W()" << endl;}W(const W& w) {cout << "W(const W& w)" << endl;}~W(){cout << "~W()" << endl;}
};
void f1(W w) {
}
int main()
{f1(W()); //先构造一个匿名对象,然后作为参数 传值传参过去return 0;
}结果:
依然没调用拷贝构造。
看看程序怎么运行的:

还是刚刚讲的,这是因为编译器的优化,将 构造+拷贝构造 直接优化成了 一步构造。
结论:一个连续的表达式步骤中,连续构造一般都会被优化。
传值返回
可以优化的情况:
class W
{
public://构造函数W(int w=0) :_w(w){cout << "W()" << endl;}//拷贝构造函数W(const W& w) :_w(w._w){cout << "W(const W& w)" << endl;}//析构函数~W(){cout << "~W()" << endl;}
private:int _w;
};
W func() {W ret; //1次构造return ret; //1次拷贝构造:将ret的值通过拷贝构造返回
}
int main()
{W w1=func(); //W w1=……仍是一次拷贝构造。所以按理说是“1构造+2拷贝构造”return 0;
}然而实际上只进行了“1构造+1拷贝构造”:

为什么拷贝构造从2次变成了1次?
原来,这也是编译器的优化,它会将两个拷贝构造,优化成一个。
这里用图说明一下:

不能优化的情况
上面这种情况和下面的这种要区分,下面这种是不能优化的:
class W
{
public://构造函数W(int w=0) :_w(w){cout << "W()" << endl;}//拷贝构造函数W(const W& w) :_w(w._w){cout << "W(const W& w)" << endl;}//赋值运算符W& operator=(const W& w) {cout << "W& operator=(const W& w)" << endl;if (this != &w) {_w = w._w;}return *this;}//析构函数~W(){cout << "~W()" << endl;}
private:int _w;
};
W func() {W ret;return ret;
}
int main()
{W w1; w1 = func(); //赋值接收对象return 0;
}这种是分4步进行的:

可见,赋值接收对象 不如 拷贝构造的方式接收。后者可以被优化。
总结
1.连续的 构造和拷贝构造 会被优化成 直接调用构造。(分步的就无法优化了)
2.产生的临时变量往往会被优化掉。
题目的解析
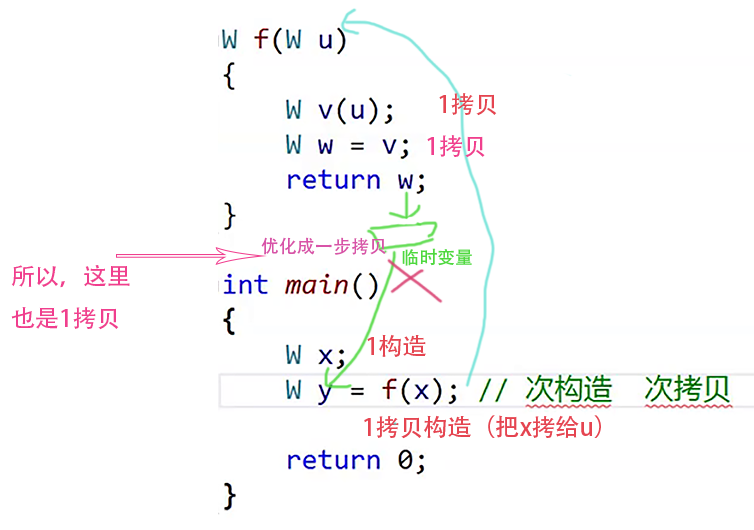
我们现在回过头看看一开始那道题:

首先,W x;是1次构造。
然后,f(x)会把x的值拷贝给u,是1次拷贝构造。
在函数f(W u)里,v的实例化是1次拷贝构造.
w究竟是拷贝构造还是赋值的呢?因为w原先不存在,所以不是赋值,是1次拷贝构造。
return w;(这里最易错) 原本是要拷贝产生临时变量,再用临时变量拷贝构造出y的。但经过编译器的优化,升级成一步拷贝构造。
所以,一共1构造+4拷贝构造。
把这题升级一下:
几次构造?几次拷贝构造?

和上题同理,只不过这次return w将连续的三步优化成一步。
答案:1次构造 7次拷贝构造