C#，《小白学程序》第二十六课：大数乘法（BigInteger Multiply）的Toom-Cook 3算法及源程序

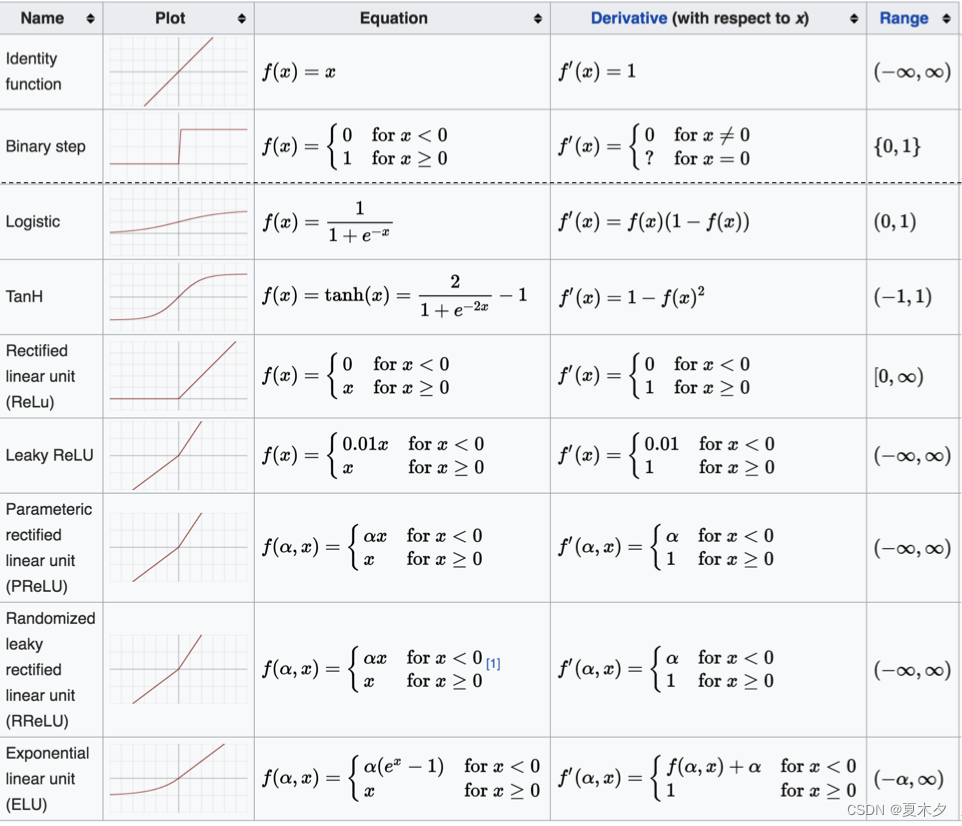
凑数的，仅供参考。

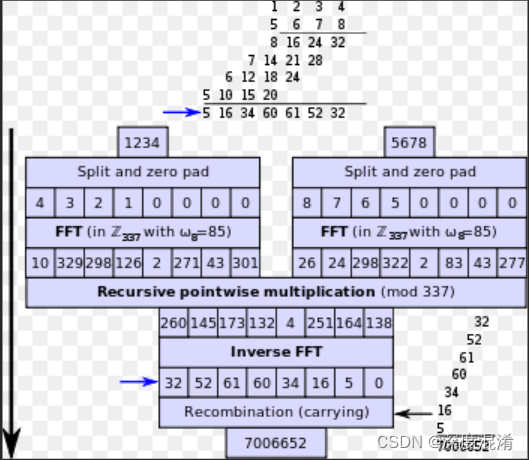
1 文本格式

/// <summary>
/// 《小白学程序》第二十六课：大数（BigInteger）的Toom-Cook 3乘法
/// Toom-Cook 3-Way Multiplication
/// </summary>
/// <param name="a"></param>
/// <param name="b"></param>
/// <returns></returns>
public static string toom_cook3_multiply(string a, string b)
{
    int n = Math.Max(a.Length, b.Length);
    int[] ra = string_to_digitals(a, n);
    int[] rb = string_to_digitals(b, n);
    toom_cook3_process_00(ra, rb, out int[] rz);
    toom_cook3_carry(rz, n * 2);
    return digitals_to_string(rz);
}

/// <summary>
/// 短数字的乘法（常规乘法，小学生算法）
/// </summary>
/// <param name="a"></param>
/// <param name="b"></param>
/// <param name="z"></param>
private static void toom_cook3_normal(int[] a, int[] b, ref int[] z)
{
    int n = a.Length;
    for (int j = 0; j < n; j++)
    {
        for (int i = 0; i < n; i++)
        {
            z[j + i] += a[i] * b[j];
        }
    }
}

/// <summary>
/// 完全按原始C++代码改写；运行成功；
/// </summary>
/// <param name="a"></param>
/// <param name="b"></param>
/// <param name="z"></param>
private static void toom_cook3_process_01(int[] a, int[] b, out int[] z)
{
    int n = a.Length;
    int n1 = n * 1 / 3;
    int n2 = n * 2 / 3;
    int n3 = n * 3 / 3;
    int n4 = n * 4 / 3;

    z = new int[n * 2];
    if (n <= 9)
    {
        toom_cook3_normal(a, b, ref z);
        return;
    }

    // int *a0 = &a[0];
    // Multiplicand / right side array pointer
    int a0 = 0;
    // int *a1 = &a[tLen / 3];
    // Multiplicand / central array pointer
    int a1 = n1;
    // int *a2 = &a[tLen * 2/ 3];
    // Multiplicand / left side array pointer
    int a2 = n2;// n * 2 / 3;

    // int *b0 = &b[0];
    // Multiplier / right side array pointer
    int b0 = 0;
    // int *b1 = &b[tLen / 3];
    // Multiplier / central array pointer
    int b1 = n1;
    // int *b2 = &b[tLen * 2 / 3];
    // Multiplier / left side array pointer
    int b2 = n2;// n * 2 / 3;

    // int *c0 = &z[(tLen / 3) * 0];
    int[] c0 = new int[n2];
    int[] c1 = new int[n2];
    // int *c2 = &z[(tLen / 3) * 2];
    int[] c2 = new int[n2];
    int[] c3 = new int[n2];
    // int *c4 = &z[(tLen / 3) * 4];
    int[] c4 = new int[n2];

    int[] a_m2 = new int[n1];  // a(-2)
    int[] a_m1 = new int[n1];  // a(-1)
    int[] a_0 = new int[n1];   // a(0)
    int[] a_1 = new int[n1];   // a(1)
    int[] a_inf = new int[n1]; // a(inf)
    int[] b_m2 = new int[n1];  // b-2)
    int[] b_m1 = new int[n1];  // b-1)
    int[] b_0 = new int[n1];   // b(0)
    int[] b_1 = new int[n1];   // b(1)
    int[] b_inf = new int[n1]; // b(inf)

    // ==== a(-2) = 4 * a2 - 2 * a1 + a0, b(-2) = 4 * b2 - 2 * b1 + b0
    for (int i = 0; i < n1; i++)
    {
        a_m2[i] = (a[a2 + i] << 2) - (a[a1 + i] << 1) + a[a0 + i];
        b_m2[i] = (b[b2 + i] << 2) - (b[b1 + i] << 1) + b[b0 + i];
    }
    // ==== c(-2) = a(-2) * b(-2)
    toom_cook3_process_01(a_m2, b_m2, out int[] c_m2);

    // ==== a(-1) = a2 - a1 + a0, b(-1) = b2 - b1 + b0
    for (int i = 0; i < n1; i++)
    {
        a_m1[i] = a[a2 + i] - a[a1 + i] + a[a0 + i];
        b_m1[i] = b[b2 + i] - b[b1 + i] + b[b0 + i];
    }
    // ==== c(-1) = a(-1) * b(-1)
    toom_cook3_process_01(a_m1, b_m1, out int[] c_m1);

    // ==== a(0) = a0, b(0) = b0
    for (int i = 0; i < n1; i++)
    {
        a_0[i] = a[a0 + i];
        b_0[i] = b[b0 + i];
    }
    // ==== c(0) = a(0) * b(0)
    toom_cook3_process_01(a_0, b_0, out int[] c_0);

    // ==== a(1) = a2 + a1 + a0, b(1) = b2 + b1 + b0
    for (int i = 0; i < n1; i++)
    {
        a_1[i] = a[a2 + i] + a[a1 + i] + a[a0 + i];
        b_1[i] = b[b2 + i] + b[b1 + i] + b[b0 + i];
    }
    // ==== c(1) = a(1) * b(1)
    toom_cook3_process_01(a_1, b_1, out int[] c_1);

    // ==== a(inf) = a2, b(inf) = b2
    for (int i = 0; i < n1; i++)
    {
        a_inf[i] = a[a2 + i];
        b_inf[i] = b[b2 + i];
    }

    // ==== c(inf) = a(inf) * b(inf)
    toom_cook3_process_01(a_inf, b_inf, out int[] c_inf);

    // ==== c4 = 6 * c(inf) / 6
    for (int i = 0; i < n2; i++)
    {
        c4[i] = c_inf[i];
    }
    // ==== c3 = -c(-2) + 3 * c(-1) - 3 * c(0) + c(1) + 12 * c(inf) / 6
    for (int i = 0; i < n2; i++)
    {
        c3[i] = -c_m2[i];
        c3[i] += (c_m1[i] << 1) + c_m1[i];
        c3[i] -= (c_0[i] << 1) + c_0[i];
        c3[i] += c_1[i];
        c3[i] += (c_inf[i] << 3) + (c_inf[i] << 2);
        c3[i] /= 6;
    }
    // ==== c2 = 3 * c(-1) - 6 * c(0) + 3 * c(1) - 6 * c(inf) / 6
    for (int i = 0; i < n2; i++)
    {
        c2[i] = (c_m1[i] << 1) + c_m1[i];
        c2[i] -= (c_0[i] << 2) + (c_0[i] << 1);
        c2[i] += (c_1[i] << 1) + c_1[i];
        c2[i] -= (c_inf[i] << 2) + (c_inf[i] << 1);
        c2[i] /= 6;
    }
    // ==== c1 = c(-2) - 6 * c(-1) + 3 * c(0) + 2 * c(1) - 12 * c(inf) / 6
    for (int i = 0; i < n2; i++)
    {
        c1[i] = c_m2[i];
        c1[i] -= (c_m1[i] << 2) + (c_m1[i] << 1);
        c1[i] += (c_0[i] << 1) + c_0[i];
        c1[i] += (c_1[i] << 1);
        c1[i] -= (c_inf[i] << 3) + (c_inf[i] << 2);
        c1[i] /= 6;
    }
    // ==== c0 = 6 * c(0) / 6
    for (int i = 0; i < n2; i++)
    {
        c0[i] = c_0[i];
    }
    // ==== z = c4 * x^4 + c3 * x^3 + c2 * x^2 + c1 * x + c0
    for (int i = 0; i < n2; i++)
    {
        z[i + n4] += c4[i];
        z[i + n3] += c3[i];
        z[i + n2] += c2[i];
        z[i + n1] += c1[i];
        z[i] += c0[i];
    }
}
 


    /// <summary>
    /// 乘积和的进位计算
    /// </summary>
    /// <param name="a"></param>
    /// <param name="n"></param>
    /// <exception cref="Exception"></exception>
    private static void toom_cook3_carry(int[] a, int n)
    {
        int cr = 0;
        for (int i = 0; i < n; i++)
        {
            a[i] += cr;
            if (a[i] < 0)
            {
                cr = -(-(a[i] + 1) / 10 + 1);
            }
            else
            {
                cr = a[i] / 10;
            }
            a[i] -= cr * 10;
        }
        if (cr != 0)
        {
            // Overflow
            throw new Exception("OVERFLOW! cr=" + cr);
        }
    }

2 代码格式

/// <summary>
/// 《小白学程序》第二十六课：大数（BigInteger）的Toom-Cook 3乘法
/// Toom-Cook 3-Way Multiplication
/// </summary>
/// <param name="a"></param>
/// <param name="b"></param>
/// <returns></returns>
public static string toom_cook3_multiply(string a, string b)
{int n = Math.Max(a.Length, b.Length);int[] ra = string_to_digitals(a, n);int[] rb = string_to_digitals(b, n);toom_cook3_process_00(ra, rb, out int[] rz);toom_cook3_carry(rz, n * 2);return digitals_to_string(rz);
}/// <summary>
/// 短数字的乘法（常规乘法，小学生算法）
/// </summary>
/// <param name="a"></param>
/// <param name="b"></param>
/// <param name="z"></param>
private static void toom_cook3_normal(int[] a, int[] b, ref int[] z)
{int n = a.Length;for (int j = 0; j < n; j++){for (int i = 0; i < n; i++){z[j + i] += a[i] * b[j];}}
}/// <summary>
/// 完全按原始C++代码改写；运行成功；
/// </summary>
/// <param name="a"></param>
/// <param name="b"></param>
/// <param name="z"></param>
private static void toom_cook3_process_01(int[] a, int[] b, out int[] z)
{int n = a.Length;int n1 = n * 1 / 3;int n2 = n * 2 / 3;int n3 = n * 3 / 3;int n4 = n * 4 / 3;z = new int[n * 2];if (n <= 9){toom_cook3_normal(a, b, ref z);return;}// int *a0 = &a[0];// Multiplicand / right side array pointerint a0 = 0;// int *a1 = &a[tLen / 3];// Multiplicand / central array pointerint a1 = n1;// int *a2 = &a[tLen * 2/ 3];// Multiplicand / left side array pointerint a2 = n2;// n * 2 / 3;// int *b0 = &b[0];// Multiplier / right side array pointerint b0 = 0;// int *b1 = &b[tLen / 3];// Multiplier / central array pointerint b1 = n1;// int *b2 = &b[tLen * 2 / 3];// Multiplier / left side array pointerint b2 = n2;// n * 2 / 3;// int *c0 = &z[(tLen / 3) * 0];int[] c0 = new int[n2];int[] c1 = new int[n2];// int *c2 = &z[(tLen / 3) * 2];int[] c2 = new int[n2];int[] c3 = new int[n2];// int *c4 = &z[(tLen / 3) * 4];int[] c4 = new int[n2];int[] a_m2 = new int[n1];  // a(-2)int[] a_m1 = new int[n1];  // a(-1)int[] a_0 = new int[n1];   // a(0)int[] a_1 = new int[n1];   // a(1)int[] a_inf = new int[n1]; // a(inf)int[] b_m2 = new int[n1];  // b-2)int[] b_m1 = new int[n1];  // b-1)int[] b_0 = new int[n1];   // b(0)int[] b_1 = new int[n1];   // b(1)int[] b_inf = new int[n1]; // b(inf)// ==== a(-2) = 4 * a2 - 2 * a1 + a0, b(-2) = 4 * b2 - 2 * b1 + b0for (int i = 0; i < n1; i++){a_m2[i] = (a[a2 + i] << 2) - (a[a1 + i] << 1) + a[a0 + i];b_m2[i] = (b[b2 + i] << 2) - (b[b1 + i] << 1) + b[b0 + i];}// ==== c(-2) = a(-2) * b(-2)toom_cook3_process_01(a_m2, b_m2, out int[] c_m2);// ==== a(-1) = a2 - a1 + a0, b(-1) = b2 - b1 + b0for (int i = 0; i < n1; i++){a_m1[i] = a[a2 + i] - a[a1 + i] + a[a0 + i];b_m1[i] = b[b2 + i] - b[b1 + i] + b[b0 + i];}// ==== c(-1) = a(-1) * b(-1)toom_cook3_process_01(a_m1, b_m1, out int[] c_m1);// ==== a(0) = a0, b(0) = b0for (int i = 0; i < n1; i++){a_0[i] = a[a0 + i];b_0[i] = b[b0 + i];}// ==== c(0) = a(0) * b(0)toom_cook3_process_01(a_0, b_0, out int[] c_0);// ==== a(1) = a2 + a1 + a0, b(1) = b2 + b1 + b0for (int i = 0; i < n1; i++){a_1[i] = a[a2 + i] + a[a1 + i] + a[a0 + i];b_1[i] = b[b2 + i] + b[b1 + i] + b[b0 + i];}// ==== c(1) = a(1) * b(1)toom_cook3_process_01(a_1, b_1, out int[] c_1);// ==== a(inf) = a2, b(inf) = b2for (int i = 0; i < n1; i++){a_inf[i] = a[a2 + i];b_inf[i] = b[b2 + i];}// ==== c(inf) = a(inf) * b(inf)toom_cook3_process_01(a_inf, b_inf, out int[] c_inf);// ==== c4 = 6 * c(inf) / 6for (int i = 0; i < n2; i++){c4[i] = c_inf[i];}// ==== c3 = -c(-2) + 3 * c(-1) - 3 * c(0) + c(1) + 12 * c(inf) / 6for (int i = 0; i < n2; i++){c3[i] = -c_m2[i];c3[i] += (c_m1[i] << 1) + c_m1[i];c3[i] -= (c_0[i] << 1) + c_0[i];c3[i] += c_1[i];c3[i] += (c_inf[i] << 3) + (c_inf[i] << 2);c3[i] /= 6;}// ==== c2 = 3 * c(-1) - 6 * c(0) + 3 * c(1) - 6 * c(inf) / 6for (int i = 0; i < n2; i++){c2[i] = (c_m1[i] << 1) + c_m1[i];c2[i] -= (c_0[i] << 2) + (c_0[i] << 1);c2[i] += (c_1[i] << 1) + c_1[i];c2[i] -= (c_inf[i] << 2) + (c_inf[i] << 1);c2[i] /= 6;}// ==== c1 = c(-2) - 6 * c(-1) + 3 * c(0) + 2 * c(1) - 12 * c(inf) / 6for (int i = 0; i < n2; i++){c1[i] = c_m2[i];c1[i] -= (c_m1[i] << 2) + (c_m1[i] << 1);c1[i] += (c_0[i] << 1) + c_0[i];c1[i] += (c_1[i] << 1);c1[i] -= (c_inf[i] << 3) + (c_inf[i] << 2);c1[i] /= 6;}// ==== c0 = 6 * c(0) / 6for (int i = 0; i < n2; i++){c0[i] = c_0[i];}// ==== z = c4 * x^4 + c3 * x^3 + c2 * x^2 + c1 * x + c0for (int i = 0; i < n2; i++){z[i + n4] += c4[i];z[i + n3] += c3[i];z[i + n2] += c2[i];z[i + n1] += c1[i];z[i] += c0[i];}
}/// <summary>/// 乘积和的进位计算/// </summary>/// <param name="a"></param>/// <param name="n"></param>/// <exception cref="Exception"></exception>private static void toom_cook3_carry(int[] a, int n){int cr = 0;for (int i = 0; i < n; i++){a[i] += cr;if (a[i] < 0){cr = -(-(a[i] + 1) / 10 + 1);}else{cr = a[i] / 10;}a[i] -= cr * 10;}if (cr != 0){// Overflowthrow new Exception("OVERFLOW! cr=" + cr);}}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/135638.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

【AI视野·今日NLP 自然语言处理论文速览 第三十五期】Mon, 18 Sep 2023

【AI视野·今日NLP 自然语言处理论文速览 第三十五期】Mon, 18 Sep 2023

AI视野今日CS.NLP 自然语言处理论文速览 Mon, 18 Sep 2023 Totally 51 papers &#x1f449;上期速览✈更多精彩请移步主页 Daily Computation and Language Papers "Merge Conflicts!" Exploring the Impacts of External Distractors to Parametric Knowledge Gra…
阅读更多...
6.1、Flink数据写入到文件

6.1、Flink数据写入到文件

1、前言 Flink API 提供了FileSink连接器&#xff0c;来帮助我们将数据写出到文件系统中去 版本说明&#xff1a;java1.8、flink1.17 官网链接&#xff1a;官网 2、Format Types - 指定文件格式 FileSink 支持 Row-encoded 、Bulk-encoded 两种格式写入文件系统 Row-encode…
阅读更多...
Vulnhub实战-DC9

Vulnhub实战-DC9

前言 本次的实验靶场是Vulnhub上面的DC-9&#xff0c;其中的渗透测试过程比较多&#xff0c;最终的目的是要找到其中的flag。 一、信息收集 对目标网络进行扫描 arp-scan -l 对目标进行端口扫描 nmap -sC -sV -oA dc-9 192.168.1.131 扫描出目标开放了22和80两个端口&a…
阅读更多...
GFS分布式文件系统

GFS分布式文件系统

目录 1、GFS理论 1.1、概述 1.2、GFS的基本概念和架构&#xff1a; 1.2.1. 基本概念 1.2.2. 架构&#xff1a; 1.3、GFS的基本组成部分包括&#xff1a; 1.4、GFS具有以下几个关键特点&#xff1a; 1.5、GlusterFS特点 1.6、GFS的术语 1.7、GlusterFS 采用模块化、堆…
阅读更多...
【C++】STL简介 | string类的常用接口

【C++】STL简介 | string类的常用接口

目录 STL简介 学string类前的铺垫 概念 为什么要学string类 string类的底层&#xff08;了解&#xff09; 编码表的故事 string类的常用接口与应用 3个必掌握的构造 赋值 访问字符operator[] 初识迭代器&#xff08;iterator&#xff09; 反向迭代器 用范围for遍历…
阅读更多...
【微信小程序】swiper的使用

【微信小程序】swiper的使用

1.swiper的基本使用 <jxz-header></jxz-header> <view class"banner"><swiperprevious-margin"30rpx"autoplayinterval"2000"indicator-dotsindicator-color"rgba(0,0,0,0.3)"indicator-active-color"#bda…
阅读更多...
每日一题 337. 打家劫舍 III

每日一题 337. 打家劫舍 III

难度&#xff1a;中等 整体思路相当于是前两天的方法倒过来&#xff0c;毕竟二叉树最常用的解法就是递归倒推 对于每一颗子树&#xff0c;他必定有一种最大的盗取方法&#xff0c;但是只有它的 root 的盗取情况才会影响到 root 的父节点&#xff0c;即如果收益最大的盗取方法…
阅读更多...
虚拟线上发布会带来颠覆性新体验，3D虚拟场景直播迸发品牌新动能

虚拟线上发布会带来颠覆性新体验，3D虚拟场景直播迸发品牌新动能

虚拟线上发布会是近年来在数字化营销领域备受关注的形式&#xff0c;而随着虚拟现实技术的不断进步&#xff0c;3D虚拟场景直播更成为了品牌宣传、推广的新选择。可以说&#xff0c;虚拟线上发布会正在以其颠覆性的新体验&#xff0c;为品牌带来全新的活力。 1.突破时空限制&am…
阅读更多...
竞赛选题 基于深度学习的人脸性别年龄识别 - 图像识别 opencv

竞赛选题 基于深度学习的人脸性别年龄识别 - 图像识别 opencv

文章目录 0 前言1 课题描述2 实现效果3 算法实现原理3.1 数据集3.2 深度学习识别算法3.3 特征提取主干网络3.4 总体实现流程 4 具体实现4.1 预训练数据格式4.2 部分实现代码 5 最后 0 前言 &#x1f525; 优质竞赛项目系列&#xff0c;今天要分享的是 &#x1f6a9; 毕业设计…
阅读更多...
09MyBatisX插件

09MyBatisX插件

MyBatisX插件 在真正开发过程中对于一些复杂的SQL和多表联查就需要我们自己去编写代码和SQL语句,这个时候可以使用MyBatisX插件帮助我们简化开发 安装MyBatisX插件: File -> Settings -> Plugins -> 搜索MyBatisx插件搜索安装然后重启IDEA 跳转文件功能 由于一个项…
阅读更多...
计算机竞赛 深度学习 opencv python 公式识别(图像识别 机器视觉)

计算机竞赛 深度学习 opencv python 公式识别(图像识别 机器视觉)

文章目录 0 前言1 课题说明2 效果展示3 具体实现4 关键代码实现5 算法综合效果6 最后 0 前言 &#x1f525; 优质竞赛项目系列&#xff0c;今天要分享的是 &#x1f6a9; 基于深度学习的数学公式识别算法实现 该项目较为新颖&#xff0c;适合作为竞赛课题方向&#xff0c;学…
阅读更多...
Unity Bolt 实现UI拖拽功能

Unity Bolt 实现UI拖拽功能

最近在学习使用Bolt插件实现五代码对UGUI Image元素实现拖拽。先看效果 录制_2023_09_15_17_50_45_29 下面是实现方式介绍&#xff1a; 1&#xff1a;注册RectTransformUtility 在使用Bolt插件实现UI拖拽的功能&#xff0c;需要使用 RectTransformUtility.ScreenPointToLoca…
阅读更多...
操作系统基本概念

操作系统基本概念

目录 一、基本概述 二、操作系统的特点 &#xff08;一&#xff09;并发性&#xff08;实质是微观的串行、宏观的并行&#xff09; 1. 对比看&#xff1a;并行性 2. 单核CPU和多核CPU &#xff08;二&#xff09;共享性 &#xff08;三&#xff09;虚拟性 &#xff08;…
阅读更多...
自动化和数字化在 ERP 系统中意味着什么？

自动化和数字化在 ERP 系统中意味着什么？

毋庸置疑&#xff0c;ERP系统的作用是让工作更轻松。它可以集成流程&#xff0c;提供关键分析&#xff0c;确保你的企业高效运营。这些信息可以提高你的运营效率&#xff0c;并将有限的人力资本重新部署到更有效、更重要的需求上。事实上&#xff0c;自动化和数字化是ERP系统最…
阅读更多...
【Unity程序技巧】Unity中的单例模式的运用

【Unity程序技巧】Unity中的单例模式的运用

&#x1f468;‍&#x1f4bb;个人主页&#xff1a;元宇宙-秩沅 &#x1f468;‍&#x1f4bb; hallo 欢迎 点赞&#x1f44d; 收藏⭐ 留言&#x1f4dd; 加关注✅! &#x1f468;‍&#x1f4bb; 本文由 秩沅 原创 &#x1f468;‍&#x1f4bb; 收录于专栏&#xff1a;Uni…
阅读更多...
爬虫 — 验证码反爬

爬虫 — 验证码反爬

目录 一、超级鹰二、图片验证模拟登录1、页面分析1.1、模拟用户正常登录流程1.2、识别图片里面的文字 2、代码实现 三、滑块模拟登录1、页面分析2、代码实现&#xff08;通过对比像素获取缺口位置&#xff09; 四、openCV1、简介2、代码3、案例 五、selenium 反爬六、百度智能云…
阅读更多...
【QT】day2

【QT】day2

1.完善登录框 点击登录按钮后&#xff0c;判断账号&#xff08;admin&#xff09;和密码&#xff08;123456&#xff09;是否一致&#xff0c;如果匹配失败&#xff0c;则弹出错误对话框&#xff0c;文本内容“账号密码不匹配&#xff0c;是否重新登录”&#xff0c;给定两个按…
阅读更多...
分布式缓冲-Redis

分布式缓冲-Redis

个人名片&#xff1a; 博主&#xff1a;酒徒ᝰ. 个人简介&#xff1a;沉醉在酒中&#xff0c;借着一股酒劲&#xff0c;去拼搏一个未来。 本篇励志&#xff1a;三人行&#xff0c;必有我师焉。 本项目基于B站黑马程序员Java《SpringCloud微服务技术栈》&#xff0c;SpringCloud…
阅读更多...
神经网络 02(激活函数)

神经网络 02(激活函数)

一、激活函数 在神经元中引入了激活函数&#xff0c;它的本质是向神经网络中引入非线性因素的&#xff0c;通过激活函数&#xff0c;神经网络就可以拟合各种曲线。 如果不用激活函数&#xff0c;每一层输出都是上层输入的线性函数&#xff0c;无论神经网络有多少层&#xff0c…
阅读更多...
（vue2）面经基础版-案例效果分析

（vue2）面经基础版-案例效果分析

配路由 先配一级&#xff0c;一级里面配二级。一级路由&#xff1a;首页&#xff08;二级&#xff1a;嵌套4个小页面&#xff09;、详情页 高亮a->router-link&#xff0c;高亮效果对自带高亮类名router-link(-exact)-active设置 注&#xff1a;通过children配置项&#…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023