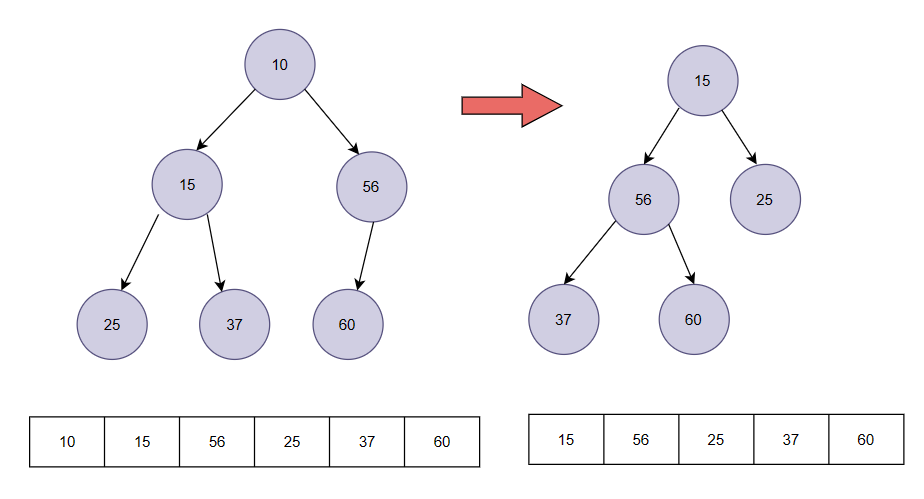
1.红黑树发明的原因

分析二叉排序树，平衡二叉树，红黑树的算法效率：

	BST	AVL Tree	Red-Black Tree
时间	1960	1962	1972
时间复杂度（增删查）	$O(n)$	$O(lo{g}_{2}n)$	$O(lo{g}_{2}n)$

1.平衡二叉树AVL的缺点

插入/删除很容易破坏“平衡”特性，需要频繁调整树的形态。

如:插入操作导致不平衡，则需要先计算平衡因子，
找到最小不平衡子树(时间开销大)，再进行LL/RR/LR/RL调整。

2.引入红黑树优化平衡二叉树

红黑树RBT:插入/删除很多时候不会破坏“红黑”特性，无需频繁调整树的形态。
即便需要调整，一般都可以在常数级时间内完成

3.红黑树和平衡二叉树的选择

• 平衡二叉树:适用于以查为主、很少插入/删除的场景
• 红黑树:适用于频繁插入、删除的场景，实用性更强

2.红黑树的定义

红黑树是二叉排序树：左子树结点值≤根结点值≤右子树结点值。

1.红黑规则

• ①每个结点或是红色，或是黑色的
• ②根节点是黑色的
• ③叶结点（外部结点、NULL结点、失败结点）均是黑色的
• ④不存在两个相邻的红结点（即红结点的父节点和孩子结点均是黑色)
• ⑤对每个结点，从该节点到任一叶结点的简单路径上，所含黑结点的数目相同

例如：

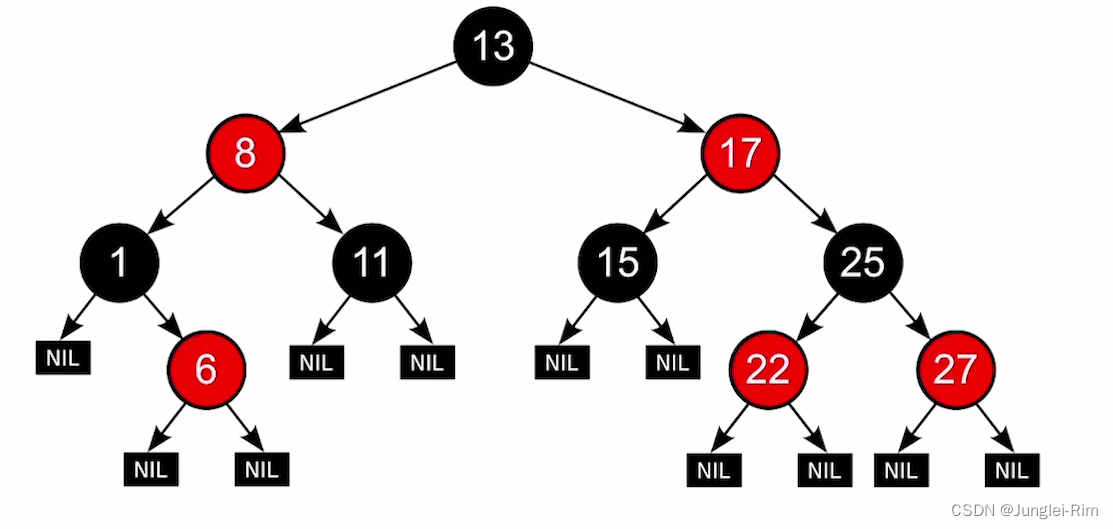
记忆口诀：“左根右，根叶黑，不红红，黑路同”。

2.结点数据结构设计

struct RBnode {//红黑树的结点定义int key ;//关键字的值RBnode* parent;//父节点指针RBnode* lchild;//左孩子指针RBnode* rChild;//右孩子指针int color;//结点颜色，如:可用0/1表示黑/红，也可使用枚举型enum表示颜色
};

3.结点的黑高

结点的黑高bh ：从某结点出发(不含该结点）到达任一空叶结点的路径上黑结点总数。

1.问：根节点黑高为h的红黑树，内部结点数（关键字）至少有多少个 ?

答：内部结点数最少的情况――总共h层黑结点的满树形态.
若根节点黑高为h，内部结点数（关键字）最少有$2^h$个。

例如：

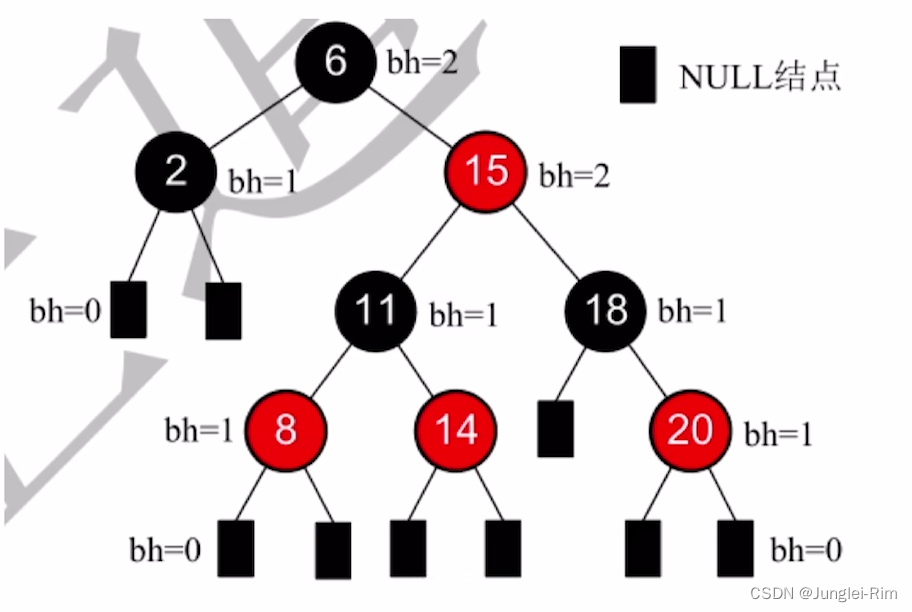
4.叶结点

在RBT中，“叶结点”通常指“失败结点”
(又名:空叶结点/NULL结点/外部结点)。

3.红黑树的性质

• 性质1:从根节点到叶结点的最长路径不大于最短路径的2倍
  证明:任何一条查找失败路径上黑结点数量都相同，而路径上不能连续出现两个红结点，即红结点只能穿插在各个黑结点中间。
• 性质2:有n个内部节点的红黑树高度h ≤ 2$lo{g}_2(n+1)$
  若红黑树总高度=h，)则根节点黑高≥$\frac{h}{2}$，因此内部结点数n>=$2^h-1$，由此推出h ≤ 2$lo{g}_2(n+1)$

1.时间复杂度

由性质2可以推出，红黑树查找操作时间复杂度=O($lo{g}_{2}n$)。

2.红黑树的查找

与BST、AVL 相同，从根出发，左小右大，
若查找到一个空叶节点，则查找失败。

4.红黑树的插入

1.插入的策略

1. 先查找，确定插入位置（原理同二叉排序树），插入新结点
2. 新结点是根：染为黑色
3. 新结点非根：染为红色
4. 若插入新结点后依然满足红黑树定义，则插入结束。
5. 若插入新结点后不满足红黑树定义，需要调整（根据叔叔结点的颜色），使其重新满足红黑树定义。

调整规则：

1 . 黑叔:旋转+染色

• LL型:右单旋，父换爷+染色
• RR型:左单旋，父换爷+染色
• LR型:左、右双旋，儿换爷+染色
• RL型:右、左双旋，儿换爷+染色

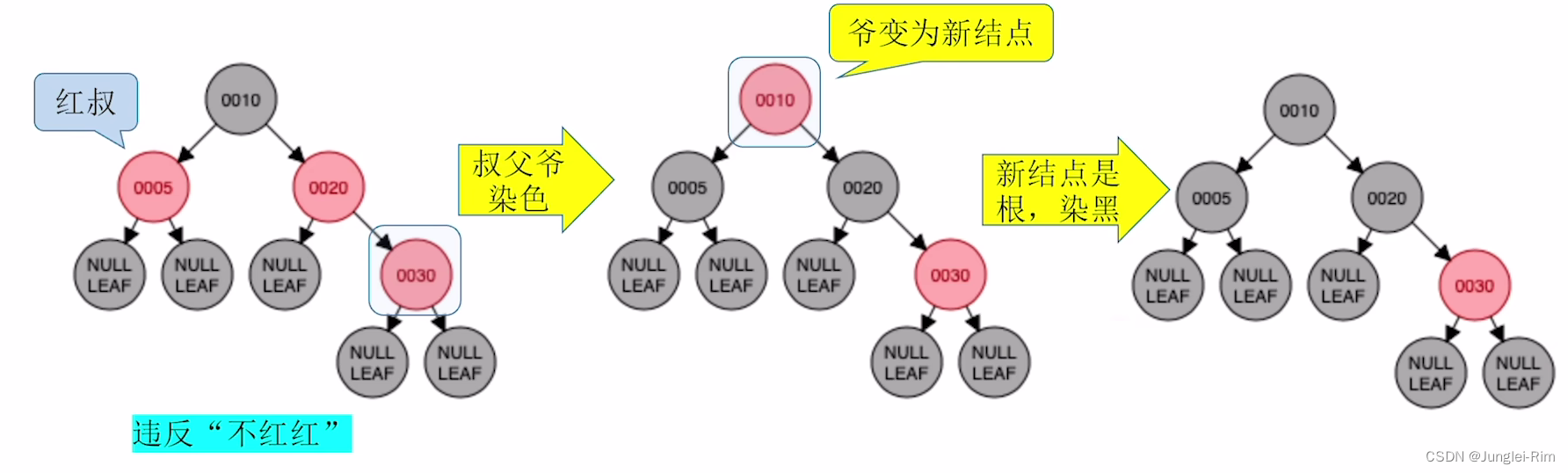
2 . 红叔:染色+变新

• 叔父爷染色，爷变为新结点
  例如：当插入元素30时的操作
  

5.红黑树的删除

1.考点

• ①红黑树删除操作的时间复杂度=$O(lo{g}_{2}n)$
• ②在红黑树中删除结点的处理方式和“二叉排序树的删除”一样
• ③按②删除结点后，可能破坏“红黑树特性”，此时需要调整结点颜色、位置，使其再次满足“红黑树特性”。