质数
质数的判定
866. 试除法判定质数 - AcWing题库
时间复杂度是logN
#include<bits/stdc++.h>
using namespace std;
int n;
bool isprime(int x)
{if(x<2) return false;for(int i=2;i<=x/i;i++){if(x%i==0) return false;}return true;
}
signed main()
{cin>>n; for(int i=1;i<=n;i++){int x;cin>>x;if(isprime(x)) puts("Yes");else puts("No");}return 0;
} 分解质因数
867. 分解质因数 - AcWing题库
#include<bits/stdc++.h>
using namespace std;
int n;
void divide(int x)
{for(int i=2;i<=x/i;i++){if(x%i==0) {int s=0;while(x%i==0) x/=i,s++;cout<<i<<" "<<s<<endl;}}if(x>1) cout<<x<<" "<<1<<endl;cout<<endl;
}
signed main()
{cin>>n; for(int i=1;i<=n;i++){int x;cin>>x;divide(x);}return 0;
} 筛质数(用线性筛,O(N)
868. 筛质数 - AcWing题库
朴素版,埃氏筛法
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
bool st[N];
int prime[N],cnt;
int n;
void getprimes(int x)
{for(int i=2;i<=x;i++){if(st[i]) continue;prime[cnt++]=i;for(int j=i+i;j<=x;j+=i) st[j]=true;}}
signed main()
{cin>>n; getprimes(n);cout<<cnt;return 0;
} 线性筛
868. 筛质数 - AcWing题库
线性筛把时间复杂度优化到O(n),就需要保证筛去一个数只用一次,保证最小质因数就可以确保这一点。
如。筛去24,24=2*12,24=3*8,显然这里2是最小质因数,如何确保不筛去3*8?
这里3*8=3*2*4,即i包含上一个prime,直接break。
只要i包含了prime就不能保证最小质因数!!
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
bool st[N];
int prime[N],cnt;
int n;
void getprimes(int x)
{for(int i=2;i<=x;i++){if(!st[i]) prime[cnt++]=i;for(int j=0;prime[j]<=x/i;j++){st[prime[j]*i]=true;if(i%prime[j]==0) break;}}}
signed main()
{cin>>n; getprimes(n);cout<<cnt;return 0;
} 约数
试除法求一个数的所有约束
869. 试除法求约数 - AcWing题库
#include<bits/stdc++.h>
using namespace std;void solve(int x)
{stack<int> s;for(int i=1;i<=x/i;i++){if(x%i==0) {cout<<i<<' ';if(i!=x/i) s.push(x/i);}}while(s.size()){cout<<s.top()<<" ";s.pop();}puts("");
}
signed main()
{int n;cin>>n;while(n--){int x;cin>>x;solve(x);}return 0;
} 约数个数//约数之和
870. 约数个数 - AcWing题库

#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
typedef long long LL;
signed main()
{int n;cin>>n;unordered_map<int,int> mp;while(n--){int x;cin>>x;for(int i=2;i<=x/i;i++){while(x%i==0){mp[i]++;x/=i;}}if(x>1) mp[x]++;}LL res=1;for(auto p:mp) res=res*(p.second+1)%mod;cout<<res<<endl; return 0;
} 871. 约数之和 - AcWing题库
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
typedef long long LL;
signed main()
{int n;cin>>n;unordered_map<int,int> mp;while(n--){int x;cin>>x;for(int i=2;i<=x/i;i++){while(x%i==0){mp[i]++;x/=i;}}if(x>1) mp[x]++;}LL res=1;for(auto p:mp){LL a=p.first,b=p.second;LL t=1;while(b--) t=(t*a+1)%mod;//秦九韶res=res*t%mod; }cout<<res<<endl; return 0;
} 最大公约数
872. 最大公约数 - AcWing题库
#include<bits/stdc++.h>
using namespace std;
int gcb(int a,int b)
{return b?gcd(b,a%b):a;
}
signed main()
{int n;cin>>n;while(n--){int a,b;cin>>a>>b;cout<<gcd(a,b)<<endl; }return 0;
}
欧拉函数
求任意一数的欧拉函数 O(n*sqrt(a))
873. 欧拉函数 - AcWing题库

#include<bits/stdc++.h>
using namespace std;signed main()
{int n;cin>>n;while(n--){int x;cin>>x;int res=x;for(int i=2;i<=x/i;i++){if(x%i==0){res=res/i*(i-1);while(x%i==0) x/=i;} }if(x>1) res=res/x*(x-1);cout<<res<<endl;}return 0;
} 求1-n中每个数的欧拉函数 O(n)
874. 筛法求欧拉函数 - AcWing题库
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int prime[N],cnt;
bool st[N];
int phi[N];//欧拉函数typedef long long LL;
signed main()
{int n;cin>>n;phi[1]=1;for(int i=2;i<=n;i++){if(!st[i]) {prime[cnt++]=i;phi[i]=i-1;//质数的欧拉函数 }for(int j=0;prime[j]<=n/i;j++){st[prime[j]*i]=true;if(i%prime[j]==0) {phi[prime[j]*i]=prime[j]*phi[i]; //括号里质因子是一样的,只是n要多乘上一个 break;}phi[prime[j]*i]=phi[i]*(prime[j]-1); //prime是质数且i不能整除prime,则说明两数没有公因数//那么prime[j]*i比i只是多了一个质因子prime[j] }}LL res=0;for(int i=1;i<=n;i++) res+=phi[i];cout<<res;return 0;
}快速幂
快速幂
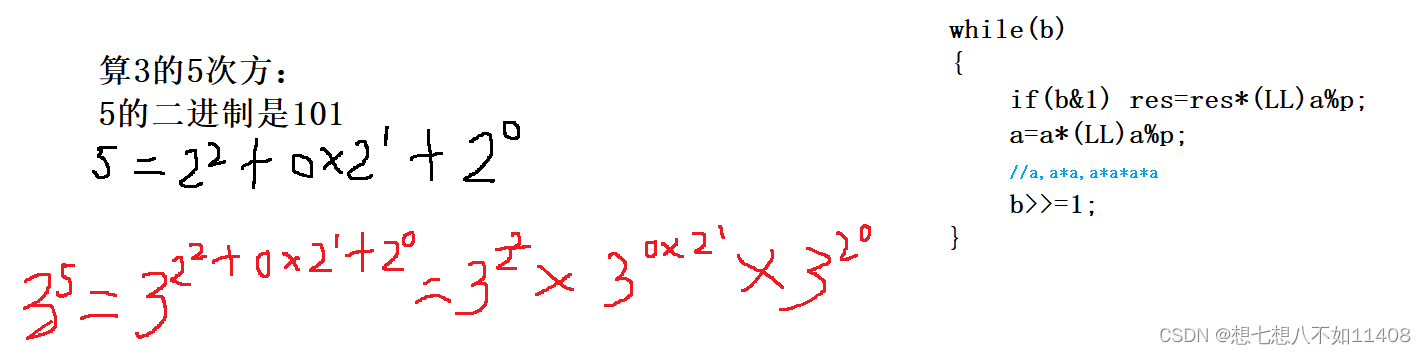
875. 快速幂 - AcWing题库
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;LL qmi(int a,int b,int p)
{LL res=1%p;while(b){if(b&1) res=res*(LL)a%p;a=a*(LL)a%p;b>>=1;}return res;
}
signed main()
{int n; cin>>n;while(n--){int a,b,p;cin>>a>>b>>p;cout<<qmi(a,b,p)<<endl; }return 0;
} 快速幂求逆元
876. 快速幂求逆元 - AcWing题库
(1)当a与p互质时,用快速幂求逆元(费马小定理):quick_power(a, b, p);
(2)当a与p不互质时,用扩展欧几里得算法求逆元:exgcd(a, p, x, y)。
概念:
 证明:费马小定理(通俗易懂) - 知乎 (zhihu.com)
证明:费马小定理(通俗易懂) - 知乎 (zhihu.com)
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;LL qmi(int a,int b,int p)
{LL res=1%p;while(b){if(b&1) res=res*(LL)a%p;a=a*(LL)a%p;b>>=1;}return res;
}
signed main()
{//当a和p不互质时无解,由于p是质数,也就只有a是p的倍数时无解 int n; cin>>n;while(n--){int a,b,p;cin>>a>>p;if(a%p==0) puts("impossible"); else cout<<qmi(a,p-2,p)<<endl; }return 0;
} 扩展欧几里得算法
扩展欧几里得算法
877. 扩展欧几里得算法 - AcWing题库
主要是递归。先正着求出gcd的值,求完之后倒着求x,y。
AcWing 877. 扩展欧几里得算法 - AcWing
#include<bits/stdc++.h>
using namespace std;int exgcd(int a,int b,int &x,int &y)
{if(b==0){x=1,y=0;return a; } int x1,y1,gcd;gcd=exgcd(b,a%b,x1,y1);x=y1,y=x1-a/b*y1;return gcd;
}signed main()
{int n;cin>>n;while(n--){int a,b,x,y;cin>>a>>b;exgcd(a,b,x,y);cout<<x<<" "<<y<<endl;}return 0;
}线性同余方程
878. 线性同余方程 - AcWing题库
想不明白主要应该是不太清楚裴属定理,看这个:裴蜀定理 - OI Wiki (oi-wiki.org)
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
int exgcd(int a,int b,int &x,int &y)
{if(b==0){x=1,y=0;return a; } int x1,y1,gcd;gcd=exgcd(b,a%b,x1,y1);x=y1,y=x1-a/b*y1;return gcd;
}signed main()
{int n;cin>>n;while(n--){int a,b,m;cin>>a>>b>>m;int x,y;int d=exgcd(a,m,x,y);if(b%d) puts("impossible");else cout<<(LL)b/d*x%m<<endl;}return 0;
}中国剩余定理
204. 表达整数的奇怪方式 - AcWing题库
基础中国剩余定理:算法学习笔记(10): 中国剩余定理 - 知乎 (zhihu.com)
好难,明天再看
高斯消元法
883. 高斯消元解线性方程组 - AcWing题库
#include<bits/stdc++.h>
using namespace std;
const int N=110;
const double eps = 1e-8;
int n;
double a[N][N];int gauss() // 高斯消元,答案存于a[i][n]中,0 <= i < n
{int c,r;//列,行for(c=0,r=0;c<n;c++)//遍历所有列 {int t=r;//最上面一个,还没确定for(int i = r ; i < n ; i ++){if( fabs(a[i][c]) > fabs(a[t][c]) ) t=i;//把最大的换上去 } if(fabs(a[t][c])<eps) continue;//如果这个最小的是0,跳过 for(int i=c;i<=n;i++) swap(a[t][i],a[r][i]);//交换 for(int i=n;i>=c;i--) a[r][i]/=a[r][c]; //首位变成1 for(int i=r+1;i<n;i++){if(fabs(a[i][c])>eps){for(int j=n;j>=c;j--){a[i][j]-=a[r][j]*a[i][c]; } }} r ++ ;}if(r<n){for(int i=r;i<n;i++)//从没走到的一行开始{if(fabs(a[i][n])>eps) return 2;//无解 }return 1; //无穷解 }//只有一解for(int i=n-1;i>=0;i--){for(int j=i+1;j<n;j++){a[i][n]-=a[i][j]*a[j][n];}} return 0;
}signed main()
{cin>>n;for(int i=0;i<n;i++){for(int j=0;j<n+1;j++){cin>>a[i][j]; }} int t=gauss();if (t == 2) puts("No solution");else if (t == 1) puts("Infinite group solutions");else{for (int i = 0; i < n; i ++ )printf("%.2lf\n", a[i][n]);}return 0;
} 从1开始存的版本。
#include<bits/stdc++.h>
using namespace std;
const int N=110;
const double eps=1e-8;
int n;
double a[N][N];int gauss()
{int r=1,c=1;//行列,r<=n,c<=n+1for(r=1,c=1;c<=n;c++) //遍历每一列 {int t=r;//记录行 for(int i=t;i<=n;i++){if(fabs(a[i][c]>fabs(a[t][c]))) t=i; }if(fabs(a[t][c])<eps) continue;//走了几列同时代表确定了几行 for(int i=c;i<=n+1;i++) swap(a[t][i],a[r][i]);for(int i=n+1;i>=c;i--) a[r][i]/=a[r][c];for(int i=r+1;i<=n;i++)//对每一行 {if(fabs(a[i][c])<eps) continue;//如果这个是0,不操作for(int j=n+1;j>=c;j--){a[i][j]-=a[r][j]*a[i][c]; } } r++;}if(r<n+1){for(int i=r;i<=n;i++){if(fabs(a[i][n+1])>eps) return 0;//无解 }return 2;//无穷解 }for(int i=n-1;i>=1;i--){for(int j=i+1;j<=n+1;j++){a[i][n+1]-=a[j][n+1]*a[i][j]; } } return 1;
}
signed main()
{cin>>n; for(int i=1;i<=n;i++){for(int j=1;j<=n+1;j++){cin>>a[i][j];}}int t=gauss();if(t==0) puts("No solution");else if(t==2) puts("Infinite group solutions");else{for(int i=1;i<=n;i++) printf("%.2lf\n",a[i][n+1]);}return 0;
}884. 高斯消元解异或线性方程组 - AcWing题库
#include<bits/stdc++.h>
using namespace std;
const int N=110;int n;
int a[N][N];void guass()
{int r,c;for(r=1,c=1;c<=n;c++)//枚举列 {int t=r;for(int i=r;i<=n;i++){if(a[i][c]){t=i;break;} }if(a[t][c]==0) continue;//说明第c列都是0 for(int i=c;i<=n+1;i++) swap(a[r][i],a[t][i]);for(int i=r+1;i<=n;i++){if(a[i][c]==0) continue;for(int j=c;j<=n+1;j++){a[i][j]^=a[r][j]; } } r++;}if(r<n+1)//说明等式左边都是0,判断等式右边即可 {for(int i=r;i<=n;i++){if(a[i][n+1]!=0)//无解 {puts("No solution");return; }} puts("Multiple sets of solutions");return;}//输出结果for(int i=n-1;i>=1;i--){for(int j=i+1;j<=n+1;j++){a[i][n+1]^=a[i][j]*a[j][n+1]; } } for(int i=1;i<=n;i++){cout<<a[i][n+1]<<endl;}
}
signed main()
{cin>>n; for(int i=1;i<=n;i++){for(int j=1;j<=n+1;j++){cin>>a[i][j];}}guass(); return 0;
}求组合数
885. 求组合数 I - AcWing题库
1<=b<=a<=2000
#include<bits/stdc++.h>
using namespace std;
const int N=2010,mod=1e9+7;
int a[N][N];void init()
{for(int i=0;i<N;i++){for(int j=0;j<=i;j++){if(j==0) a[i][j]=1;else a[i][j]=(a[i-1][j]+a[i-1][j-1])%mod;}}
}
signed main()
{init();int n;cin>>n;while(n--){int c,b;cin>>c>>b;cout<<a[c][b]<<endl;}return 0;
}886. 求组合数 II - AcWing题库
1<=b<=a<=1e5
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e5+10,mod=1e9+7;int fact[N],infact[N];
int qmi(int a,int k,int p)
{int res=1;while(k){if(k&1) res=(LL)res*a%p;a=(LL)a*a%p;k>>=1;}return res;
}
signed main()
{fact[0]=infact[0]=1;for(int i=1;i<N;i++){fact[i]=(LL)fact[i-1]*i%mod;infact[i]=(LL)infact[i-1]*qmi(i,mod-2,mod)%mod; }int n; cin>>n;while(n--){int a,b;cin>>a>>b;cout<<(LL)fact[a]*infact[b]%mod*infact[a-b]%mod<<endl;}return 0;
}