目录
题目:
示例:
分析:
代码:
题目:
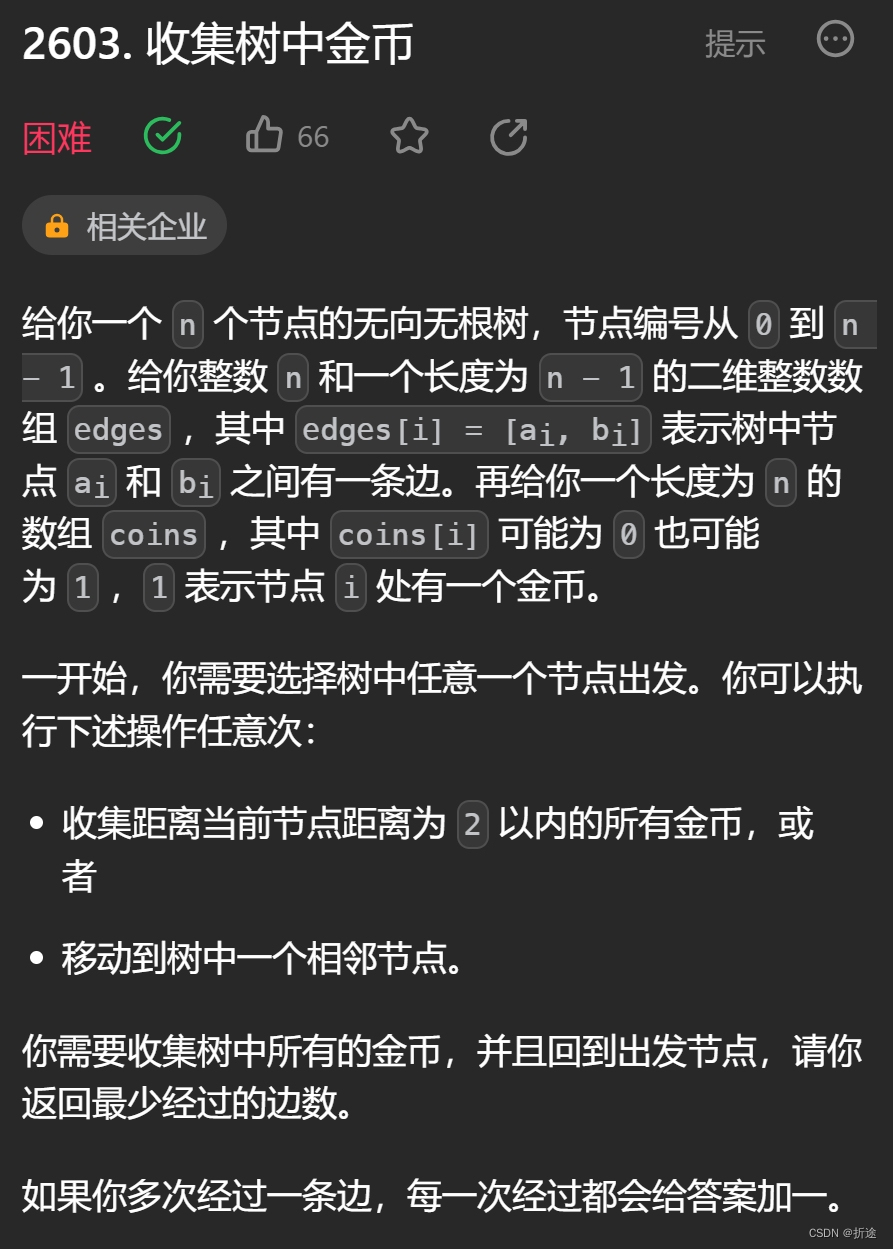
示例:
分析:
题目给我们一棵树,不过这棵树不是普通的树,而是无向无根树。给我们一个二维数组表示节点之间的连接关系,以及一个一维数组表示每个节点是否有金币。
我们可以从任何一个节点出发,并且可以收集距离两格的节点的金币,每次可以移动到相邻的节点。问我们要收集完所有的金币并且最终要回到起点,最少需要移动几次。
首先,题目说了这是一棵树,所以是不存在环的,两个节点之间连通的路径只会有唯一的一条。
因此我们不管选择哪一个节点当起点,都是可以到达任意一个节点的。
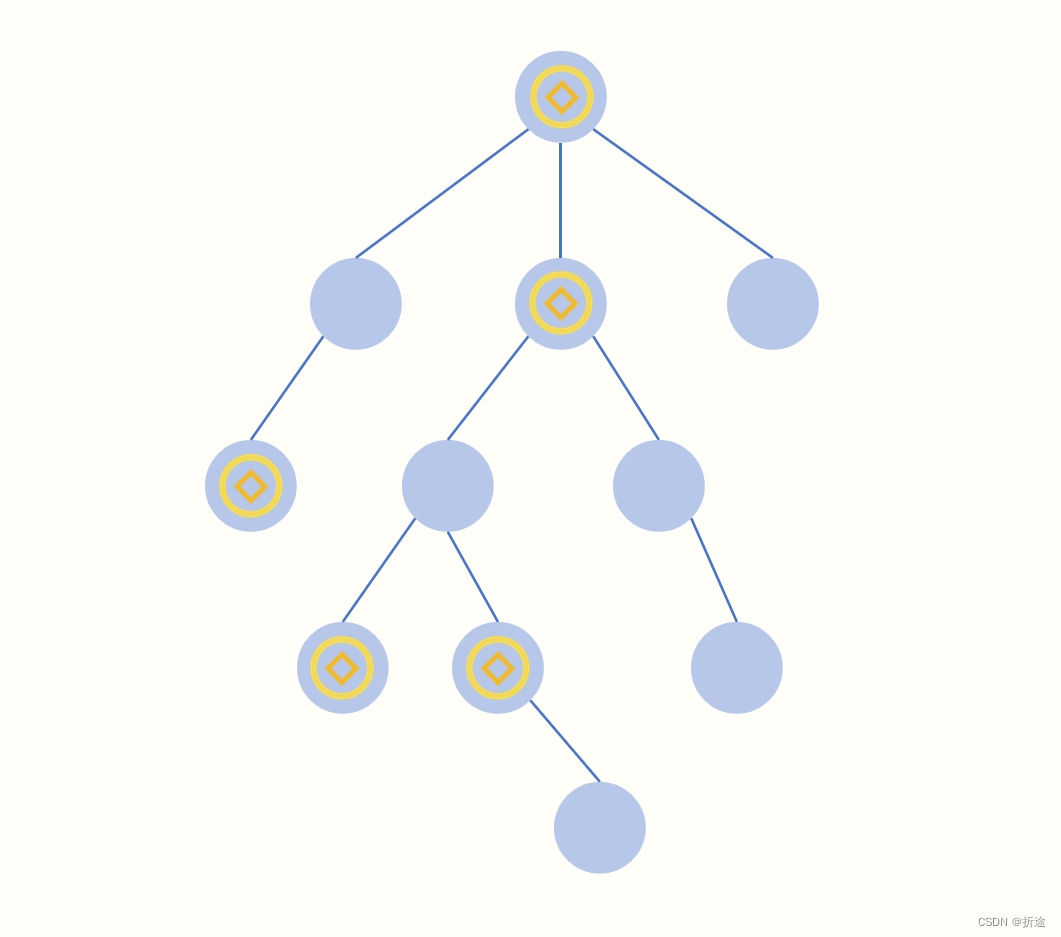
我们需要获取所有的金币,那么如果一个节点没有金币,并且这个节点是叶子节点,那么我们是不是可以将这个节点直接从树中移除,因为我们根本不需要走到这个节点。
我们把能删除的节点都删除了,是不是就说明剩下的节点都是我们需要走到或是收集金币的节点。
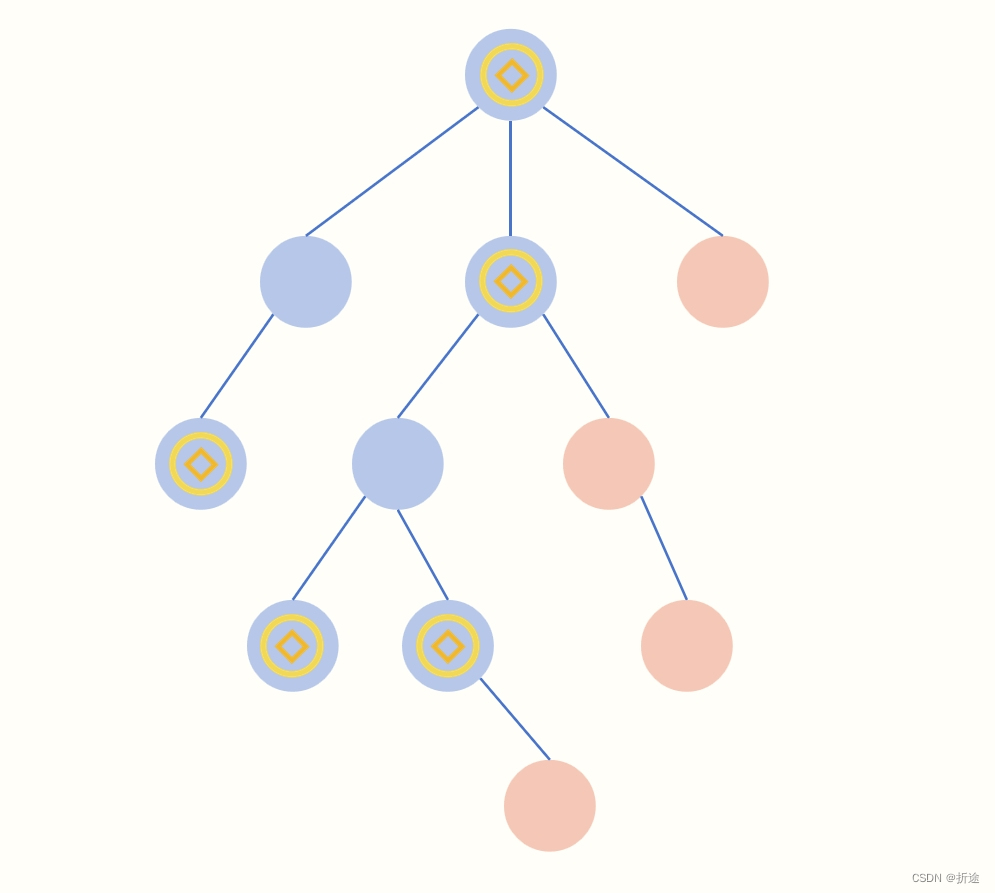
如果我们把整棵树剪到只剩下我们必须要走到的节点之后,答案就剩下节点数-1再乘2了。
为什么呢?
题目要求我们必须在收集完金币之后再返回原点,我们有n个必须到达的节点,由于这是树,是没有环的,因此节点之间的连线一共是n-1条。一来一回每个线段要走两次,所以答案是(n-1)*2
问题就变成了我们怎么把树的节点剪到只剩下我们必须要走的节点。
首先,没有金币的叶子节点我们是可以先删除的。判断依据也简单,如果一个节点没有金币,并且和这个节点连接的其他节点只有一个,那么它就是没有金币的叶子节点,可以把它删除。并且删除某个节点之后可能会诞生出新的无金币叶子节点,因此我们删除节点之后还需要判断一下与这个节点连接的节点是否也是无金币叶子节点,也就是延伸性地删除节点。
那么怎么删除呢,我们可没有构建出树来。
我们其实不需要真的删除。我们之前分析过了,答案就是剪枝后的节点数减1再乘2。我们可以当成一开始的树就是我们剪枝后的树,把答案初始化成总的节点数减1再乘2。每次我们删除一个节点就等于是移除了一个线段,把答案减2即可,这样就当成是删除一个节点了。
初步移除了没有金币的叶子节点之后剩下的节点就是我们要达到的节点或者是要收集金币的节点了。
我们把剩下的树看成是图,那么图边缘一圈的节点一定都是有金币的。

我们收集金币的时候可以距离金币节点两格,因此我们可以再一次把图的外围两层节点删除,不过删除是有条件的,最外层的叶子节点可以直接删除,不过第二层的节点我们得判断删除了外层节点后,第二层的节点是不是叶子节点,如果是我们才可以删除。
最终我们每次删除节点之后,都将答案-2,最终就是要返回出去的答案了。
不过最后还有一个问题,那就是如果整个树都是可以移除的,那么根据我们刚才说的每删除一个节点就把答案-2,而我们答案初始化是总的节点数减1再乘2,这样答案就变成了-2,因此最后我们做个判断,如果答案小于0,我们就返回0,反之就正常返回求出的答案。
代码:
class Solution {
public:unordered_map<int,vector<int>>pic; //记录节点连接图unordered_map<int,int>rel; //记录每个节点的邻接数量关系int collectTheCoins(vector<int>& coins, vector<vector<int>>& edges) {int n=coins.size();int res=2*(n-1); //答案初始化成图中线段数乘2,表示每个线段都要走两边//建图for(auto& edge:edges){if(pic.find(edge[0])==pic.end()) pic[edge[0]]=vector<int>(0);if(pic.find(edge[1])==pic.end()) pic[edge[1]]=vector<int>(0);pic[edge[0]].push_back(edge[1]);pic[edge[1]].push_back(edge[0]);rel[edge[0]]++;rel[edge[1]]++;}queue<int> q;//删除无金币的叶子节点(可延伸)for(int i=0;i<n;i++){if(coins[i]==0 && rel[i]==1) q.push(i);}while(!q.empty()){res-=2; //减少一个线段,答案减2,因为默认每个线段走两次.int cur=q.front();q.pop();for(int i:pic[cur]){if(--rel[i]==1&&coins[i]==0) q.push(i);}}//确定到有金币的叶子节点的范围.for(int i=0;i<n;i++){if(coins[i]==1&&rel[i]==1) q.push(i);}res-=2*q.size();//减少叶子节点,不延伸(因为可以收集距离两格的金币,所以可以在边缘处再缩小一圈)while(!q.empty()){int x=q.front();q.pop();for(int j:pic[x]){if(--rel[j]==1) res-=2;}}if(res>0) return res;return 0;}
};







![[设计模式] 浅谈SOLID设计原则](https://img-blog.csdnimg.cn/f845bb46162944a4b7f3f8e7292cf2aa.png)