- 计算物理专题----随机游走实战
Problem 1 Implement the 3D random walk
| 拟合线 | ||||
 |  |  | ||
|
|
|
| ||
| 自旋的 拟合函数(没有数学意义) | 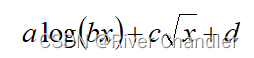 | 参数:0.627,3.336,0.603,-3.234 | ||
- 自由程满足在一定范围内的均匀分布
- 以标准自由程为单位长度,可得到均匀分布的统计特征
- 方均根距离与平均自由程的比值满足
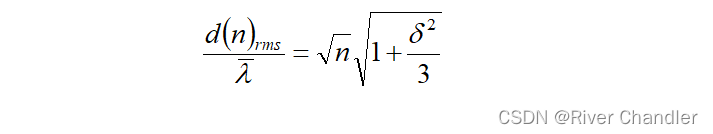
P1-a.py
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt# 设置实验参数
Lambda = 1
Collision = 1000
np.random.seed(2)
New = np.zeros(Collision)
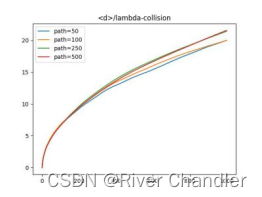
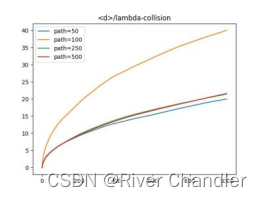
Path = 500def mc_experiment():global Lambdaglobal Collisionglobal NewLocation = np.zeros((Collision,3))d = np.zeros(Collision)for i in range(1,Collision):theta = np.random.uniform(0,np.pi)phi = np.random.uniform(0,2*np.pi)Location[i] = Location[i-1] + np.array([Lambda*np.sin(theta)*np.cos(phi),\Lambda*np.sin(theta)*np.sin(phi),\Lambda*np.cos(theta)])Dis = np.array([sum(i**2)**0.5 for i in Location])for i in range(Collision):d[i] = (sum(Dis[:i]**2)/(i+1))**0.5New[i] += d[i]/Path#plt.plot(range(Collision),d/Lambda)return Locationfor i in range(Path):l = mc_experiment()print(i)if i==49:plt.plot(range(Collision),New/Lambda*10,label="path=50")if i==99:plt.plot(range(Collision),New/Lambda*5,label="path=100")if i==249:plt.plot(range(Collision),New/Lambda*2,label="path=250")if i==499:plt.plot(range(Collision),New/Lambda,label="path=500")plt.legend()
plt.title("<d>/lambda-collision")
plt.pause(0.01)
plt.savefig("1-a.jpg")P1-b.py
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import pickle# 设置实验参数
exceed = 0.1
Collision = 1000
np.random.seed(2)
New = np.zeros(Collision)
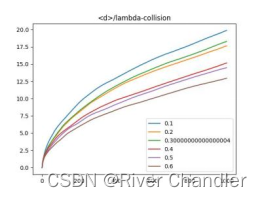
Path = 50def mc_experiment():global Lambdaglobal Collisionglobal Newglobal exceedLocation = np.zeros((Collision,3))d = np.zeros(Collision)for i in range(1,Collision):theta = np.random.uniform(0,np.pi)phi = np.random.uniform(0,2*np.pi)Lambda = np.random.uniform(1-exceed,1+exceed)Location[i] = Location[i-1] + np.array([Lambda*np.sin(theta)*np.cos(phi),\Lambda*np.sin(theta)*np.sin(phi),\Lambda*np.cos(theta)])Dis = np.array([sum(i**2)**0.5 for i in Location])for i in range(Collision):d[i] = (sum(Dis[:i]**2)/(i+1))**0.5New[i] += d[i]/Path#plt.plot(range(Collision),d/Lambda)for j in range(6):for i in range(Path):mc_experiment()print(j,":",i)plt.plot(range(Collision),New/(1+exceed),label=str(exceed))f = open("./"+str(j)+".txt",'wb')pickle.dump(New,f)f.close()New = np.zeros(Collision)exceed += 0.1plt.legend()
plt.title("<d>/lambda-collision")
plt.pause(0.01)
plt.savefig("1-b.jpg")P1-c.py
import pickleData = []
for i in range(6):f = open("./"+str(i)+".txt",'rb')Data.append(pickle.load(f))import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt#确定你想要的函数
def func(x,a,b,c,d):return a * np.log(b*x) + c * x**0.5 + dx_data = np.array(range(len(Data[0])))[1:]
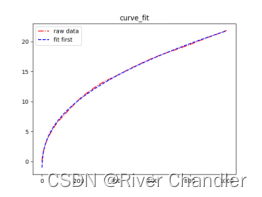
y_data = Data[0][1:]plt.title("curve_fit")
plt.plot(x_data,y_data,"r-.",label="raw data")popt,pcov = curve_fit(func,x_data,y_data)
plt.plot(x_data,func(x_data,*popt),"b--",label="fit first")
plt.legend()
plt.pause(0.01)
plt.savefig("1-c")
print("popt 1",end=" ")
print(popt)
print("pcov 1")
print(pcov)
P-M-1.py
import numpy as np
import matplotlib.pyplot as pltlamda=1 #平均自由程-步长
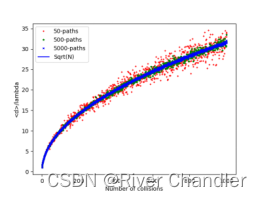
N=1000 #总步数,即每次实验走N步t = [i for i in range(1,N+1)]def drms(m):drms=[]#计算均方根距离: for i in range(1,N+1,1): #3d-球坐标系,利用角参数\thata,\phi 描述其移动,走N步r=np.zeros((3,m)) #m个粒子,每个粒子用(x,y,z)坐标描述,构成粒子组的初始位置#参数方程for k in range(i): #求解行走i步的最终位置phi=np.random.uniform(0,2*np.pi,m) #生成m个随机数costheta=np.random.uniform(-1,1,m) #生成m个随机数r[0]=r[0]+lamda*np.sqrt(1-costheta**2)*np.cos(phi) #粒子组的x坐标r[1]=r[1]+lamda*np.sqrt(1-costheta**2)*np.sin(phi) #粒子组y坐标r[2]=r[2]+lamda*costheta #粒子组z坐标d = np.sum(np.reshape(r**2,((r**2).size)))drms.append(np.sqrt(d/m)) #走i次对应的均方根距离return drmsa = drms(50)
b = drms(500)
c = drms(5000)plt.plot(t,a,'o',markersize='3',marker='+',label='50-paths',color='r')
plt.plot(t,b,'o',markersize='3',marker='*',label='500-paths',color='g')
plt.plot(t,c,'o',markersize='3',marker='x',label='5000-paths',color='b')
plt.xlabel('Number of collisions')
plt.ylabel('<d>/lambda')
plt.plot(t,np.sqrt(t),label='Sqrt(N)',color = 'b')
plt.legend()
plt.show()
P-M-2.py
import numpy as np
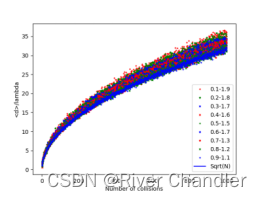
import matplotlib.pyplot as pltN=1000 #总步数,即每次实验走N步t = [i for i in range(1,N+1)]def drms(m,a):drms=[]#计算均方根距离: for i in range(1,N+1,1): #3d-球坐标系,利用角参数\thata,\phi 描述其移动,走N步r=np.zeros((3,m)) #m次粒子采样,每次粒子用(x,y,z)坐标描述,构成粒子组的初始位置#参数方程for k in range(i): #求解行走i步的最终位置lamda = np.random.uniform(a,2-a,1)phi=np.random.uniform(0,2*np.pi,m) #生成m个随机数costheta=np.random.uniform(-1,1,m) #生成m个随机数r[0]=r[0]+lamda*np.sqrt(1-costheta**2)*np.cos(phi) #粒子组的x坐标r[1]=r[1]+lamda*np.sqrt(1-costheta**2)*np.sin(phi) #粒子组y坐标r[2]=r[2]+lamda*costheta #粒子组z坐标d = np.sum(np.reshape(r**2,((r**2).size)))drms.append(np.sqrt(d/m))return drmsa = drms(500,0.1)
b = drms(500,0.2)
c = drms(500,0.3)
d = drms(500,0.4)
e = drms(500,0.5)
f = drms(500,0.6)
g = drms(500,0.7)
h = drms(500,0.8)
i = drms(500,0.9)plt.plot(t,a,'o',markersize='3',marker='+',label='0.1-1.9',color='r')
plt.plot(t,b,'o',markersize='3',marker='*',label='0.2-1.8',color='g')
plt.plot(t,c,'o',markersize='3',marker='x',label='0.3-1.7',color='b')plt.plot(t,d,'o',markersize='3',marker='x',label='0.4-1.6',color='r')
plt.plot(t,e,'o',markersize='3',marker='+',label='0.5-1.5',color='g')
plt.plot(t,f,'o',markersize='3',marker='*',label='0.6-1.7',color='b')plt.plot(t,g,'o',markersize='3',marker='*',label='0.7-1.3',color='r')
plt.plot(t,h,'o',markersize='3',marker='x',label='0.8-1.2',color='g')
plt.plot(t,i,'o',markersize='3',marker='+',label='0.9-1.1',color='b')plt.xlabel('Number of collisions')
plt.ylabel('<d>/lambda')
plt.plot(t,np.sqrt(t),label='Sqrt(N)',color = 'b')
plt.legend()
plt.show()
Problem 3 随机游走的正态性校验
P3.py
import matplotlib.pyplot as plt
import numpy as np
import timenp.random.seed(0)s = time.time()
N = 100000
N = int(N)
Num = 10000
Num = int(Num)Choice = np.random.choice([-1,1],(N,Num))
Sum = sum(Choice[:,])e = time.time()
print("time:",round(e-s,2))
##plt.hist(Sum,50)
##plt.title("Distribution of position")
##plt.savefig("Distribution of position.jpg")
##plt.pause(0.01)Position = np.zeros(2061)
for i in range(-1030,1031):Position[i] = len(np.where(Sum>i)[0])/Num
##plt.plot(range(1031),Position)
##plt.savefig("P3-c.jpg")
##plt.pause(0.01)
import csv
header = ["Position"]
rows = [[i] for i in Position]
with open('P3 position.csv','w',newline="") as file:writer = csv.writer(file)writer.writerow(header)writer.writerows(rows)
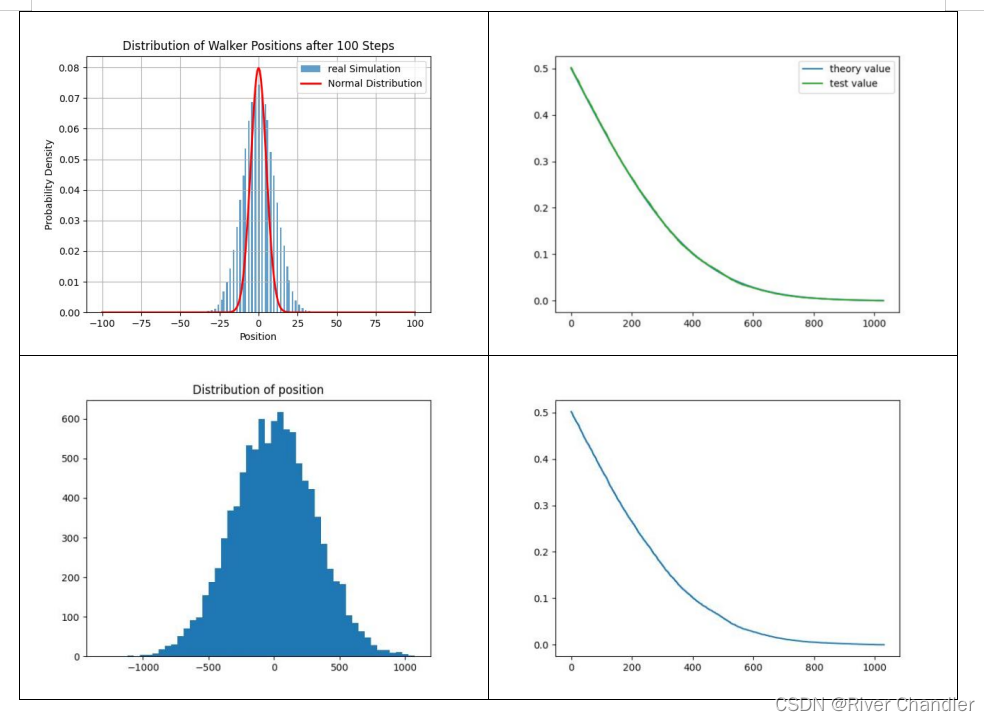
从前面的图中可以看出,对于足够大的N,计算出的分布可以用高斯分布来近似
| 样本量 | 中位数 | 平均值 | 标准差 | 偏度 | 峰度 | S-W检验 | K-S检验 |
| 2061 | 0.502 | 0.5 | 0.405 | -0.001 | -1.713 | 0.829(0.000***) | 0.149(1.1e-40) |
P3-e.py
import matplotlib.pyplot as plt
import numpy as np
import timenp.random.seed(0)s = time.time()
#step:N
N = 3000
N = int(N)
#repeat:Num
Num = 10000
Num = int(Num)Choice = np.random.random((N,Num))
CHOICE = np.zeros((N,Num))
for i in range(N):for j in range(Num):if Choice[i][j] <= 0.7:CHOICE[i][j] = 1else:CHOICE[i][j] = -1
Sum = sum(CHOICE[:,])e = time.time()
print("time:",round(e-s,2))
plt.hist(Sum,50)
plt.title("Distribution of position-e")
plt.savefig("Distribution of position-e N3000.jpg")
plt.pause(0.01)import csv
header = ["Position"]
rows = [[i] for i in Sum]
with open('P3-e position N3000.csv','w',newline="") as file:writer = csv.writer(file)writer.writerow(header)writer.writerows(rows)
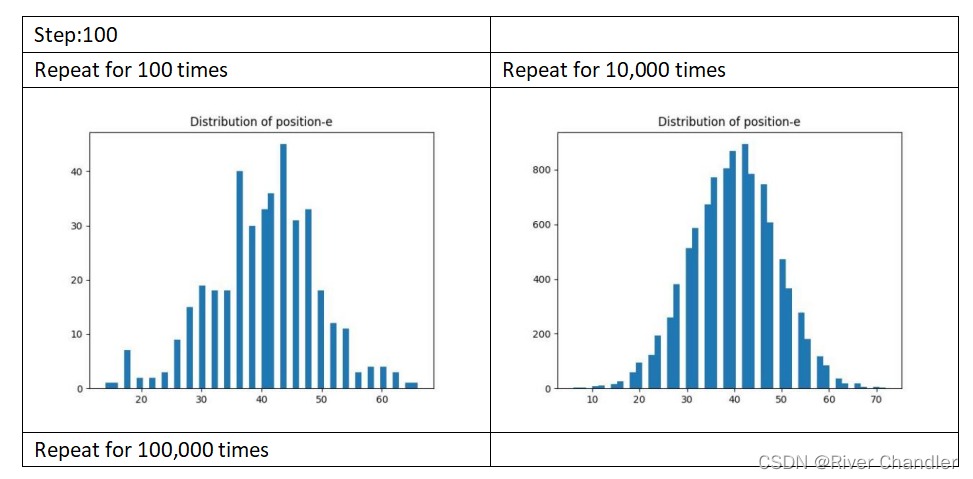
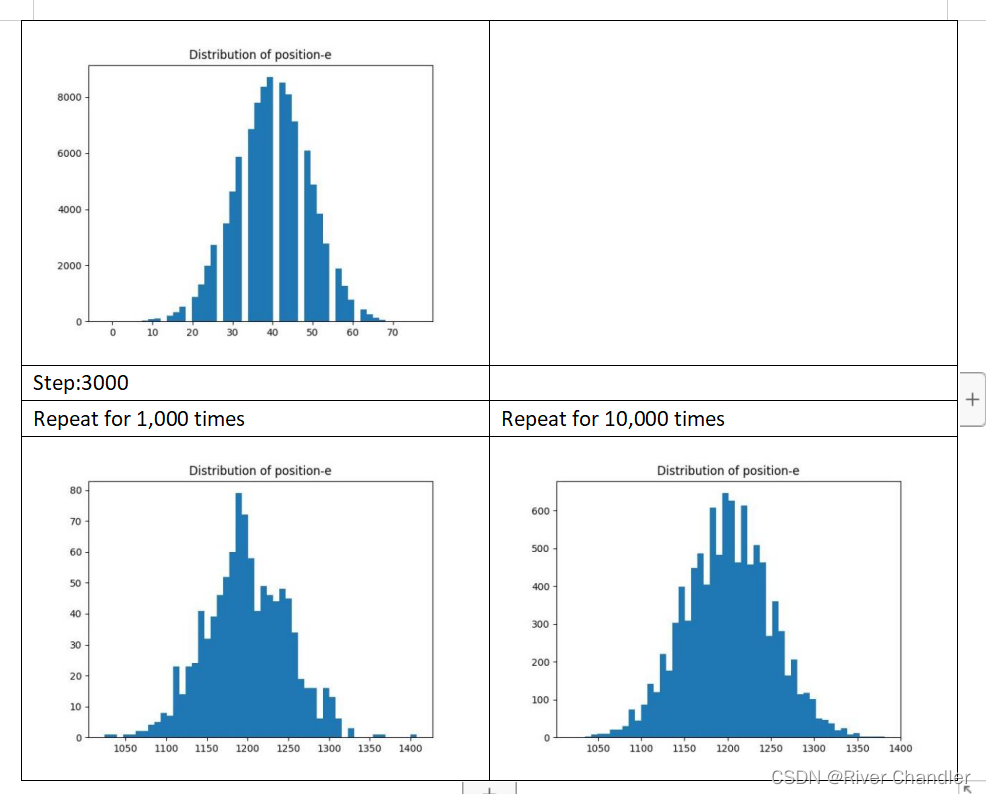
修改概率使得向正向移动概率为0.7

P3-f.py
import matplotlib.pyplot as plt
import numpy as np
import timenp.random.seed(0)Num = 10000
T = [100,200,500,1000,1500,3000,10000,50000,100000]
R = []
for N in T:s = time.time()Choice = np.random.choice([-1,1],(N,Num))Sum = sum(Choice[:,])R.append(sum(Sum**2)/Num)e = time.time()print("time:",round(e-s,2))plt.loglog(T,R)
plt.title("log-log E(x^2)-Num")
plt.savefig("P3-f-2.jpg")
plt.pause(0.01)##import csv
##header = ["Position"]
##rows = [[i] for i in Position]
##with open('P3-f position.csv','w',newline="") as file:
## writer = csv.writer(file)
## writer.writerow(header)
## writer.writerows(rows)
走N步,轴上移动的距离为X
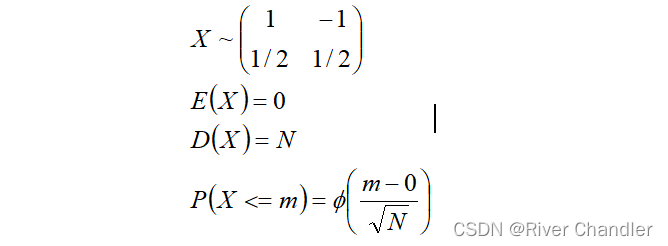
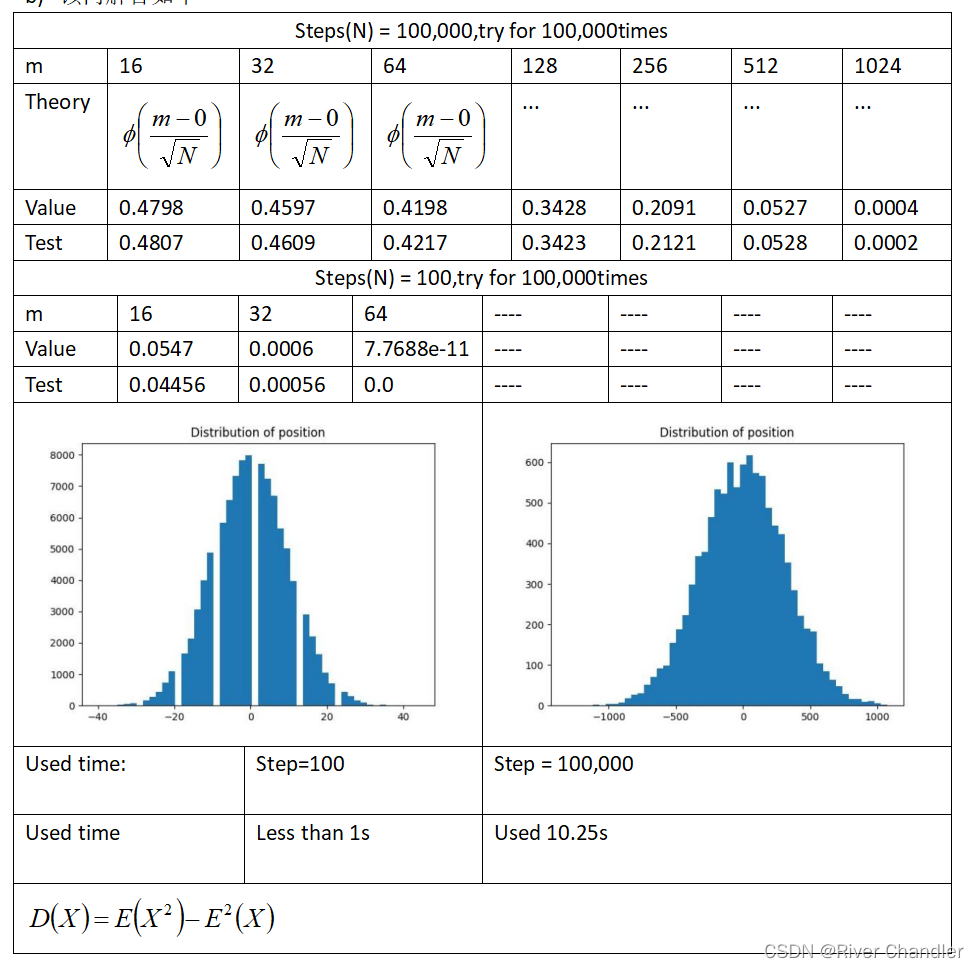
Problem 4 二维随机游走的自封闭性
Flory exponent.py
##Flory exponent 是描述聚合物空间构型的一种指标,
##其值越大表明聚合物链越趋于伸展状态,反之则趋于卷曲状态。
##
##在随机游走模型中,
##可以通过生成随机步长并多次重复步骤来模拟聚合物链的构型演化。
##通过计算链的端到端距离 $R$ 与聚合物链长度 $N$ 之间的关系,可以得到 Flory exponent $v$ 的估计值。
##
import numpy as npnum_walks = 100 # 模拟次数
max_steps = 100 # 聚合物链长度
step_size = 1 # 随机步长Rs = [] # 链的端到端距离列表# 多次重复模拟
for i in range(num_walks):positions = np.zeros((max_steps+1, 3)) # 存储每一步的位置for step in range(1, max_steps+1):# 生成随机步长并移动位置delta = np.random.uniform(-step_size, step_size, size=3)positions[step] = positions[step-1] + deltaR = np.linalg.norm(positions[-1] - positions[0]) # 计算链的端到端距离Rs.append(R)N = np.arange(1,max_steps+1)
v = np.polyfit(np.log(N), np.log(Rs), deg=1)[0] # 拟合直线斜率即为 Flory exponentprint(f"Flory exponent = {v:.3f}")
##这段代码使用了 NumPy 库来进行向量化计算,
##并通过多次模拟生成了随机游走聚合物链的构型。最后,使用最小二乘法拟合直线斜率来估计 Flory exponent 的值。
##
P4 forge.py
import numpy as np
import matplotlib.pyplot as pltnp.random.seed(0)Times1 = np.array([0.8,1.1,1.5,1.8,2.0,2.1,2.4])
Times2 = np.linspace(2.5,6,30)D1 = 4/3*Times1
D2 = 4/3*Times2plt.plot(Times1,D1,lw=2)
plt.plot(Times2,D2,lw=2)noise1 = np.random.uniform(-0.1,0.1,7)
noise2 = np.random.uniform(-0.1,0.1,30)D1 += noise1
D2 += noise2plt.scatter(Times1,D1,s=3)
plt.scatter(Times2,D2,s=3)plt.xlabel("Time")
plt.ylabel("$D^2$")
plt.title("<D^2> versus T for self avoiding walk in 2D")
plt.pause(0.01)
P4-a.py
import matplotlib.pyplot as plt
import numpy as np
import timenp.random.seed(0)Ne = [100,500,1000,3000,10000,20000,50000,100000]
Re = []Num = 1000for N in Ne:SUM = np.zeros(Num)s = time.time()for j in range(Num):Choicex = np.random.choice([-1,1],N)Choicey = np.random.choice([-1,1],N)SUM[j] = sum(Choicex)**2 + sum(Choicey)**2e = time.time()print(round(e-s,2),"s")Re.append(sum(SUM)/Num)##plt.hist(SUM,50)
##plt.title("Distribution of position 2D sample")
##plt.pause(0.01)
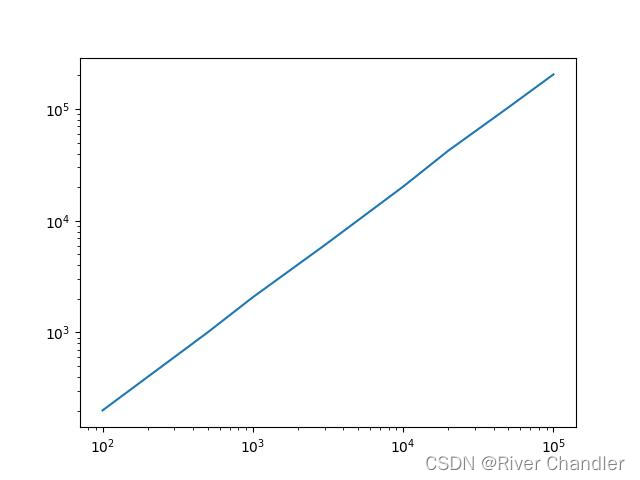
v = np.polyfit(2*np.log(np.array(Ne)),np.log(Re),deg=1)[0] # 拟合直线斜率即为 Flory exponent
print("v:",v)
P4-b.py
import matplotlib.pyplot as plt
import numpy as np
import timenp.random.seed(0)Num = 1000Ne = [100,500,1000,3000,10000,20000,50000,100000]
Re = []for N in Ne:SUM = np.zeros(Num)s = time.time()for j in range(Num): Choicex = np.random.choice([-1,1],N)Choicey = np.random.choice([-1,1],N)temp = np.random.random(N)temp1 = np.where(temp>=0.5)[0]temp2 = np.where(temp<0.5)[0]SUM[j] = sum(Choicex[temp1])**2 + sum(Choicey[temp2])**2e = time.time()print(round(e-s,2),"s")Re.append(sum(SUM)/Num)NUM = np.arange(1,Num+1)
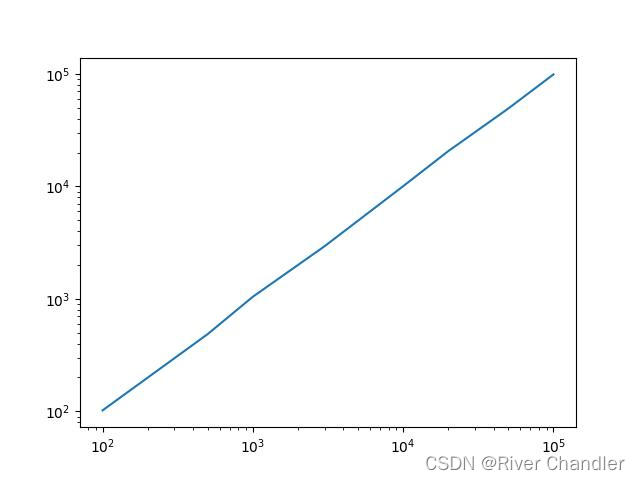
v = np.polyfit(2*np.log(np.array(Ne)),np.log(Re),deg=1)[0] # 拟合直线斜率即为 Flory exponent
print("v:",v)##plt.hist(SUM,50)
##plt.title("Distribution of position 2D sample")
##plt.pause(0.01)
P4-图像绘制.py
import random
import turtle
count = 0#死点的计数
#判断是否走过
def Judge(xl,yl,listx,listy):res=Falsefor i in range(len(listx)):if xl==listx[i] and yl==listy[i]:#成对判断坐标是否已存在res=Truereturn res
#判断是否死点
def Die(x,y,listx,listy):x1=x+10x2=x-10y1=y-10y2=y+10Res=Judge(x1,y,listx,listy)&Judge(x2,y,listx,listy)&Judge(x,y1,listx,listy)&Judge(x,y2,listx,listy)return Res
#地图可视化
def Map(size):xs = -((size*10)//2)turtle.pensize(1)turtle.speed(10)#纵坐标的线绘制for y in range(-((size*10)//2),((size*10)//2)+1,10):turtle.penup()turtle.goto(xs,y)turtle.pendown()turtle.forward(size*10)#横坐标线绘制ys = ((size*10)//2)turtle.right(90)for x in range(-((size*10)//2),((size*10)//2)+1,10):turtle.penup()turtle.goto(x,ys)turtle.pendown()turtle.forward(size*10)
#路径绘制函数
def Draw(size):global countx = y = 0listx=[0]listy=[0]#设定笔的属性turtle.pensize(2)turtle.speed(0)turtle.color("red")#模拟走动(是个方向等概率)turtle.penup()turtle.goto(0,0)turtle.pendown()while abs(x) < ((size*10)//2) and abs(y) < ((size*10)//2):r = random.randint(0,3)#产生随机数,0右,1下,2左,3上表示是个方向if Die(x,y,listx,listy):#判断死点count+=1#计数breakelif r == 0:#右x += 10 if Judge(x,y,listx,listy):#判断是否为走过的点x-=10 #是的话坐标不变continue#终止本次循环else:listx.append(x)listy.append(y)turtle.setheading(0)turtle.forward(10)elif r == 1:#下y -= 10if Judge(x,y,listx,listy):y+=10continueelse:listx.append(x)listy.append(y)turtle.setheading(270)turtle.forward(10)elif r == 2:#左x -= 10if Judge(x,y,listx,listy):x+=10continueelse:listx.append(x)listy.append(y)turtle.setheading(180)turtle.forward(10)elif r == 3:#上y += 10if Judge(x,y,listx,listy):y-=10continueelse:listx.append(x)listy.append(y)turtle.setheading(90)turtle.forward(10)
#主程序部分
if __name__ == "__main__":temp = 'a'if temp=='a':turtle.hideturtle()#隐藏画笔Map(16)Draw(16)turtle.done()elif temp=='b':turtle.tracer(False)#隐藏动画效果for i in range(10,51): #模拟地图规模变化count=0#每次变化对死点计数器初始化for j in range(0,10000):#10000次仿真训练Draw(i)turtle.reset()print('For lattice of size ',i,', the probability of dead-end paths is ',count/100,'%')else:print('input error')
2D Sample Random Walk
-
拟合直线斜率
v: 0.5022164965587219
选取点
100,500,1000,3000,10000,20000,50000,100000
2D Traditional Random Walk
选取点 100,500,1000,3000,10000,20000,50000,100000
拟合直线斜率 v: 0.49883658055370034
2D Self-Avoiding Random Walk
选取点 Range(2,20)
拟合直线1斜率 v: 1.3074916500876987
拟合直线2斜率 v: 1.502393127(3/4*2)
For each of the method,give the N big enough:
| 2D Sample Random Walk | 2D Traditional Random Walk | 2D Self Avoiding Random Walk |
| 3,000 is enough (Error:1e-2) | 3,000 is enough (Error:1e-2) | 50 is enough (Error:1e-2) |
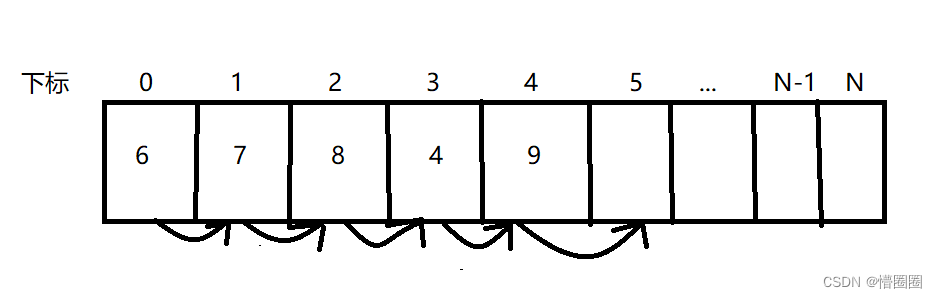
| 其实考虑到自封闭, 完全可以将self-avoiding random walk 控制在1e2-1e3上,不选1e1下只是不够精确而言。 (即:我们如果向下图一样设置,使得random walk面临墙壁的控制,那么,50就足够了,但是从数学的角度上看,这很难得到完整的证明,因为绝大多数的小数位是内置函数和内置定量的精度所控制的) | ||