排序算法-----归并排序

前言：

归并排序

1. 定义

2.算法过程讲解

2.1大致思路

2.2图解示例

拆分合成步骤

编辑

前言：

今天我们就开始学习新的排序算法----归并排序，说到归并排序，最重要的思想就是分而治之，先分后治。相较于前面所学过的排序算法，归并排序过程相对比较复杂，但是不要慌！我会详细讲解这个过程的！下面我们就一起来学习吧！

归并排序

1. 定义

归并排序是建立在归并操作上的一种有效，稳定的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并

2.算法过程讲解

2.1大致思路

已知一个数组arr[0,n-1],实现对这个数组进行拆分为arr[0,n/2]和arr[n/2+1,n-1]然后对这个数组进行进一步对半拆分，直到拆成每个分数组里面只有一个元素时，结束拆分；然后进入排序，按照拆分过程的路径进行排序合并，直到合并为一个数组的时候结束，最终得到的数组就是排序完成的数组。

归并排序是用分治思想，分治模式在每一层递归上有三个步骤：

分解（Divide）：将n个元素分成个含n/2个元素的子序列。
解决（Conquer）：用合并排序法对两个子序列递归的排序。
合并（Combine）：合并两个已排序的子序列已得到排序结果

2.2图解示例

拆分合成步骤

已知一个数组 [6,5,3,1,8,7,2,4]，要求通过归并排序进行排序

第一步，依次拆分，直到每一个分数组剩下一个元素，如下所示：

6 5 3 1 8 7 2 4

第一次拆分 6 5 3 1 8 7 2 4

第二次拆分 6 5 3 1 8 7 2 4

第三次拆分 6 5 3 1 8 7 2 4

第二步，拆分完成之后，就进行排序合并,如下所示：

6 5 3 1 8 7 2 4

第一次合并： 5 6 1 3 7 8 2 4

第二次合并： 1 3 5 6 2 4 7 8

第三次合并： 1 2 3 4 5 6 7 8

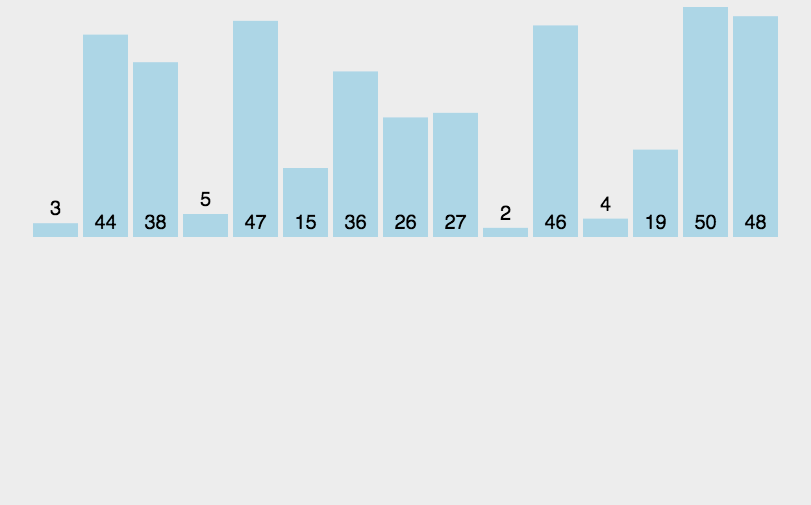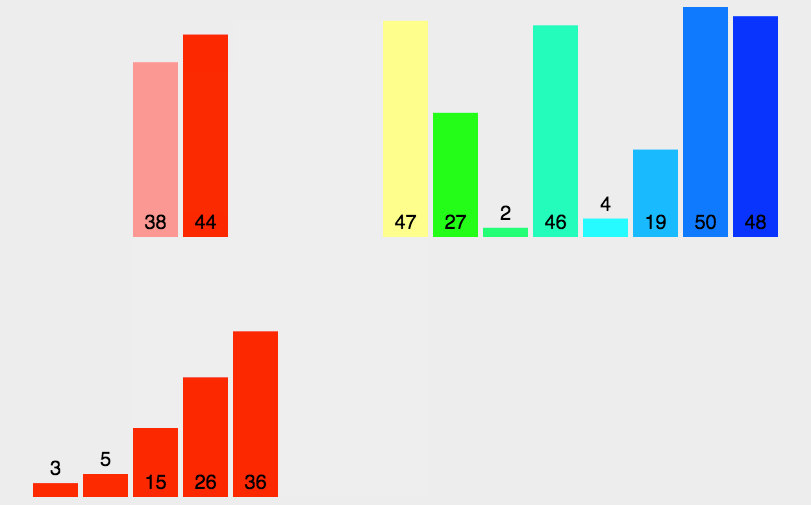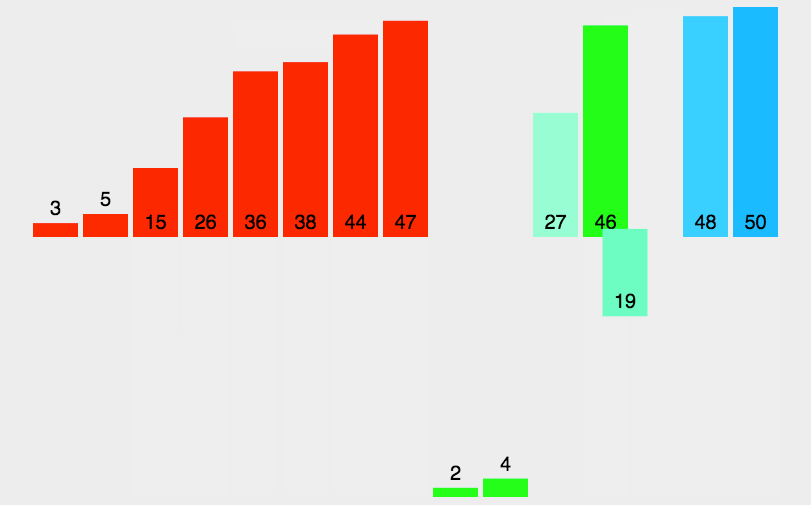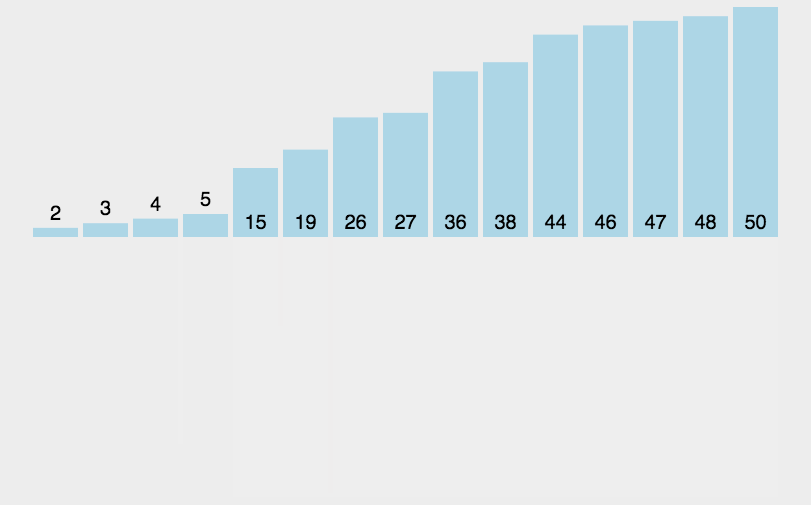
以上步骤就完成了归并排序的过程了，演示图如下所示：

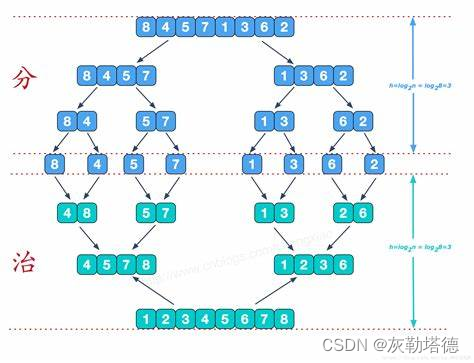
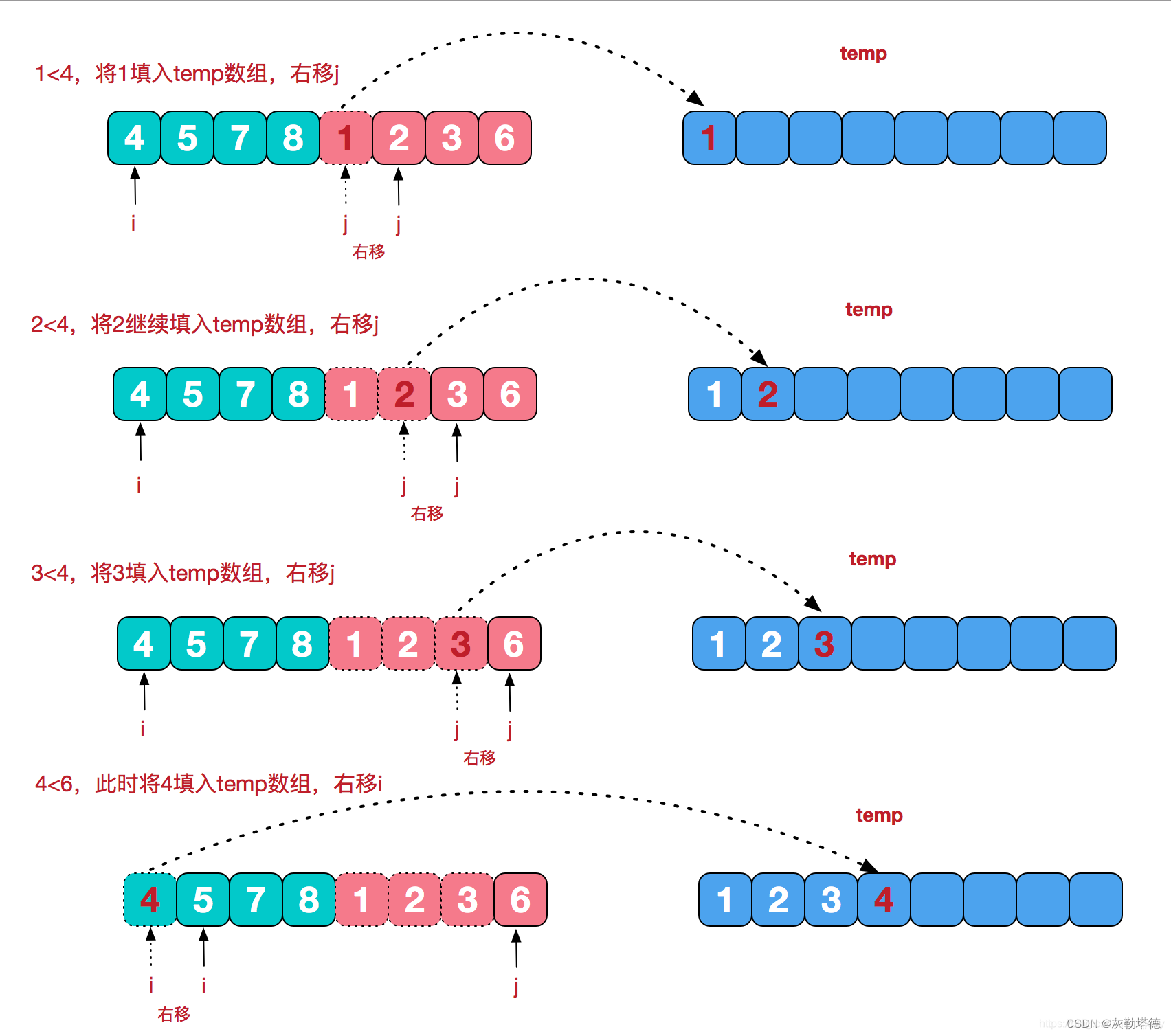
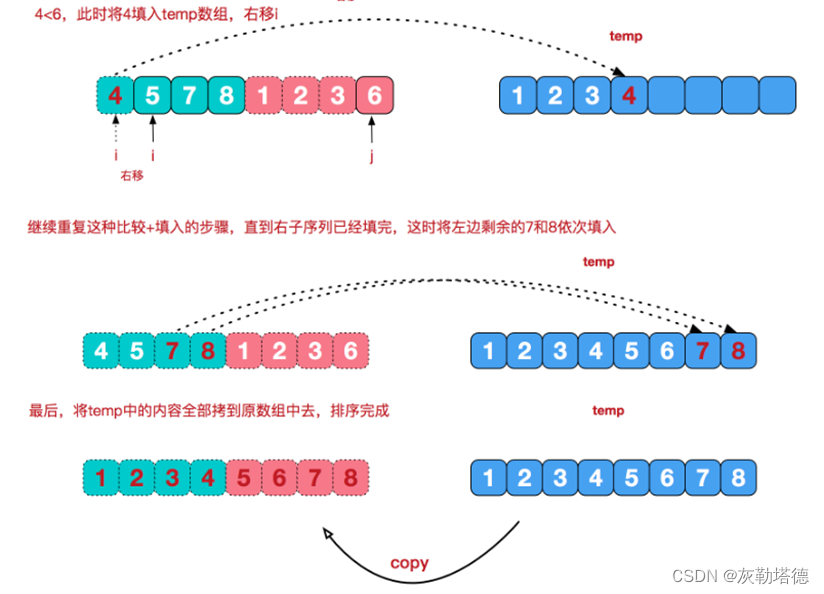动态图：

3.代码实现（C语言）

#include<stdio.h>
//归并排序
//合成排序
void merge(int* n,int *temp,int left,int mid,int rigth) {int l_pos = left;int r_pos = mid+1;int pos = left;//左右两部分数组进行比较合并while (l_pos <= mid && r_pos <= rigth) {if (n[l_pos] < n[r_pos])temp[pos++] = n[l_pos++];elsetemp[pos++] = n[r_pos++];}//如果左边还有多余的就直接补到后面去while (l_pos <= mid)temp[pos++] = n[l_pos++];//如果右边有多余的就直接补到后面去while (r_pos <= rigth)temp[pos++] = n[r_pos++];//这里只需要把原来的数组覆盖掉就行了while (left <= rigth) {n[left] = temp[left];left++;}}
//拆分与归并
void msort(int *n,int *temp,int left,int right) {if (left < right) {			int mid = (left + right) / 2;	//先拆分为两部分msort(n, temp, left, mid); //左边递归msort(n, temp, mid+1, right);//右半递归merge(n, temp, left, mid, right);	//拆分完成之后进行归并和排序}
}
//排序函数接口
void merge_sort(int* n, int length) {int* temp = (int*)malloc(sizeof(int) * length);//申请一个同样大小的辅助数组空间if (temp) {//如果申请成功msort(n, temp, 0, length-1);    //进入到排序free(temp);						//释放掉这个空间}else {printf("Space allocation failure");}
}int main() {int array[8] = { 25,24,6,65,11,43,22,51 };printf("排序前:");for (int i = 0; i < sizeof(array) / sizeof(int); i++) {printf("%d ", array[i]);}printf("\n排序后：");merge_sort(array, sizeof(array) / sizeof(int));for (int i = 0; i < sizeof(array) / sizeof(int); i++) {printf("%d ", array[i]);}
}
//排序前:25 24 6 65 11 43 22 51
//排序后：6 11 22 24 25 43 51 65