2013年,太老了,先不看 比较老的一篇论文,近规则铣削纹理中的自适应异常检测
1 Abstract
在钢质量控制中的应用,我们提出了图像处理算法,用于无监督地检测隐藏在全局铣削模式内的异常。因此,我们考虑了基于全局傅里叶的方法和局部剪切波分解来阻尼铣削纹理。这些基于频率的方法与空间域基于模板的自相关进行了比较。作为一种替代方法,所谓的匹配追踪是通过联合傅立叶和基于小波的字典提出的,可以同时利用全局铣削槽和局部异常的两个模型。所有这些方法都使用定量和特定领域的定性指标针对手动注释的真实世界数据集进行评估。
2 Introduction
钢的清洁度是其质量的一个重要属性。它由钢基体中非金属夹杂物的数量、大小、形态、分布和化学组成定义。这些不受欢迎的遏制是钢加工过程的固有副产品。然而,清洁因素对钢的力学性能有直接影响,因此需要不断监测。在[1]中,我们提出了一种组合铣削和光学扫描方法,用于评估原始生产输出的钢样品中不同类型非金属夹杂物的3D分布。因此,通过铣削刀将钢样品切成数百层。在本文中,我们将介绍和评估图像处理技术,用于将铣削模式的周期性背景纹理与非金属夹杂、收缩孔和微裂纹等钢基体中包含的各种相关异常分离。这是一个具有挑战性的任务,因为铣削纹理是实际机械钢性能、铣削工具磨损、铣削机的振动、铣削刀具的旋转和前进速度、铣削刀具的旋转和前进速度、照明特性、插值和拼接伪影的复杂相互作用的结果,这是由于图像捕获、相机设备的噪声特性和许多其他其他因素。因此,准周期铣削纹理中总是有一些变化,因此结果只是近正则的。因此,我们的目标是检测异常,我们松散地定义为与通常的铣削纹理的偏差,同时承认铣削纹理本身本质上是不同的。我们所有的图像分割方法都是考虑到异常的这种模糊定义而设计的。然而,在评估部分,我们将针对一组手动标记的图像测试算法,以评估它们在仅检测验证异常方面的实际有效性。
A.问题陈述
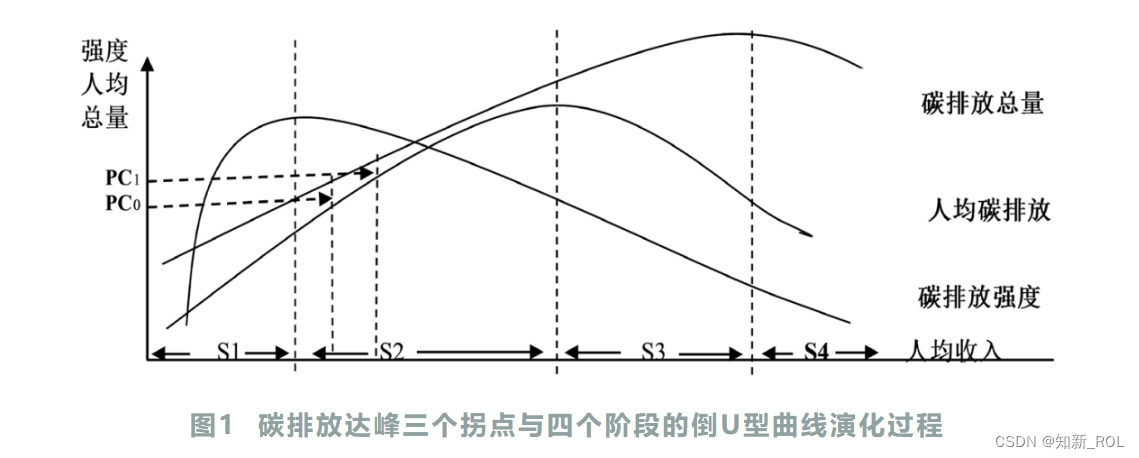
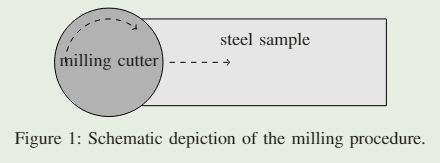
铣削刀具示意图如图1所示。铣削工具不断旋转,同时向前移动,以磨表面。因此,在整个钢表面创建了一个周期性的铣削纹理模式。当表面图像转换为频域时,可以最好地评估该信号的周期性,如图2所示。因此,不同的基于频率的变换显示了铣削纹理与非金属夹杂物(圆形缺陷)的质量不同的分离。例如,在D4小波变换下,它们与较高的频段很好地分离,而Haar小波变换仍然显示与高频异常相关的系数。在下文中,我们希望利用信号中的这些类型的规律,以便将铣削纹理与异常分离。因此,需要一种数据驱动和高度自适应的方法,因为即使是转换后的信号仍然有噪声,因为铣削纹理的唯一近规则(即不完全规则)属性。
B. Previous Work
近正则纹理的问题在[2]中得到了广泛的讨论和分析。工业图像处理中表面检测领域有很多出版物,其中讨论了其他规则表面纹理中的异常检测[3]、[4]、[5]、[6]。然而,通常情况下,背景纹理被假定为均匀随机的,否则由于印刷材料的检查,它具有很高的规则质量,没有太多的图像噪声。一个值得注意的例外是网络检查领域,它在质量上接近此处讨论的纹理分离问题。然而,网络纹理通常是 2D 周期性的,并且由于它们的正交性,这些可以通过特征值 [7] 或共现矩阵 [8] 进行分析。[9]描述了一种基于频率的自滤波方法,用于常规背景模式内的异常检测。它只进行了测试在合成图像数据和我们的真实近规则纹理的结果并不令人鼓舞。

3 APPROACHES
A.基于模型的分离
假设每个表面图像可以建模为铣削槽F、非金属夹杂E和图像噪声R的叠加。在这里,我们不考虑裂纹样缺陷,因为这些缺陷与拉长的铣削槽太相似。因此,图像 B 可以定义为:B = F + E + R。
a) 匹配追踪:匹配追踪 (MP) [10] 是一种用于稀疏近似的贪心算法。该方法通过使用基函数字典找到与信号 f 最佳匹配。迭代地,选择字典(ψi)i∈i的基函数ψi,其内积|<R,ψi>|与当前残差R最大,其中初始残差是信号f本身。然后,residuum 更新为 Rnew = Rold −<Rold, ψmax i >ψmax i。重复此过程,直到满足某些终止标准,例如最大迭代次数。最后,原始信号f将稀疏地近似为最多n个基函数:
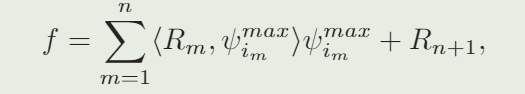
其中索引 m 描述了第 m 次迭代。
b) 全局和局部字典:我们提出了一种与两种类型的字典的匹配追踪,其中全局字典包含近似铣削纹理的基函数,局部字典包含适合拟合非金属夹杂等局部异常的基函数。假设铣削纹理是准周期性的,其行周期为2πc1c2。周期函数可以描述为正弦波和余弦波的叠加,因此逐行一维傅里叶变换为我们提供了两种构建全局字典基函数:


对于本地字典像Haar和Daubechies (D4)这样的小波是合适的。由于我们想对非常本地化的异常进行建模,我们只使用两个级别,即两个不同的缩放小波和缩放函数。因此,我们的非金属夹杂物最好用缩放函数来描述。但是,小波函数可以更好地描述边界。由于异常自然地出现在沿图像像素的每一行的未知位置,因此我们额外翻译字典中的小波和缩放函数。最后,这两个词典由欧几里得 L2 范数归一化,因此它们被平等对待。每次迭代的数值复杂度结合了小波变换的线性复杂度和表示两个模型的傅里叶变换:O(N + N log2 N )。
c) 匹配追踪异常检测:借助两个先前定义的字典,我们扩展了通常的匹配追踪,现在需要在两个全局和局部字典之间切换。因此,与本地字典完全匹配只会更新输出图像,因为我们只对仅由本地字典描述的异常感兴趣。因此,最后,我们得到了非金属夹杂物的稀疏近似E,即局部异常。引入全局字典dglobal的加权因子w,以避免局部字典DLocal的过拟合问题,因为全局铣削模式只是准周期的,因此全局字典并不总是解释最佳拟合(尽管它是预期的)。清单 1 显示了扩展匹配追踪与附加归一化的完整伪代码。
到目前为止,我们的图像模型的噪声分量 R 被忽略了。然而,由于我们的近似 E 仅包含最少数量的稀疏基函数,因此大部分噪声已经得到充分处理。对于更稳健的结果,输入图像 B 可以通过高斯核预先平滑,例如。然而,这个预处理步骤也模糊了异常的确切轮廓。总而言之,本文提出的扩展匹配追踪是基于模型的分离[11]方法的成功例子,其中分别联合利用了代表背景和前景纹理的全局和局部模型。[12]给出了类似的几何分离字典。然而,这是一个缺点,我们只能使用一维模型,因此我们忽略了图像中相邻行的空间相关性。另一方面,此属性可以实现高效和并发处理。

B.基于剪切分解
如果感兴趣的区域足够小(例如在我们的例子中为 256 × 256 或 512 × 512 像素),弯曲的铣削槽往往看起来相当直线。对于像剪切波[13]、[14]这样的方向敏感变换,我们可以建立一个类似于定向梯度直方图(HoG)的剪切波系数的直方图,其中[15]表明剪切波的性能优于HoG。其他可能的转换可能是Gabor滤波器组[16]或曲线[17],但只有剪切波可以很容易地离散化(锥体[18]上的剪切波),是可逆的,并且具有多分辨率能力。剪切波是通过额外的剪切变换对小波的扩展。因此,剪切波可以支持图像中边缘的检测,而唯一的小波变换只能表示点奇点。在我们的应用中,我们希望使用剪切波变换对图像补丁进行变换,然后将最突出的方向(即系数)设置为零或抑制,因为这些方向肯定代表了全局铣削纹理。最后,使用滤波系数和反剪切波变换再次重建输入图像。该结果图像将不受铣削纹理的影响。它只包含来自重建过程的异常和额外的伪影,这些伪影被进一步过滤,以便可以对异常进行二值化。快速剪切波变换[18]的复杂度为O(N 2 log2 N2),这是由于多次FFT乘以尺度的数量。
d)剪切波:我们使用基于频率的剪切波变换,定义为

典型的剪切函数ψ,如[18]所述。图3显示了剪切波变换的结果系数三个层次。对于更高级别的方向分辨率更精细,但更可疑的图像噪声。较亮的像素意味着较大的系数,很明显,当剪切波核的电流方向与铣削槽的角度匹配时,成功地检测到铣削模式。此外,圆形异常往往具有局部较大的响应。然而,我们也不使用这些信息,因为我们只想匹配铣削纹理。

图4:使用剪切波分解从图像2a中分割圆形缺陷,如图3所示。第一个结果4a是在k-means聚类最显著的系数后得到的。第二个结果 4b 是系数自适应邻域的加权和。在这里,背景更加均匀,重建伪影更少,从而允许稳健的二值化。
e)剪切波系数的滤波:为了自适应地检测和去除铣削槽,我们使用每个系数图像的对数欧氏L2范数的kmeans聚类。有两个簇,一个用于表示铣削模式的方向,另一个用于所有其他方向的第二个簇。属于第一个簇的所有系数都设置为零,并且图像被重建为示例,如图 4a 所示。为了减少重建伪影,由于系数的严厉切割可能属于铣削纹理,我们实现了系数的软加权,它考虑了局部邻域[19],从而产生稍微更平滑的背景纹理,如图4b所示。
由于裂纹状缺陷具有与铣削槽相似的拉长线性外观,如果它们的方向与铣削模式相似,则无法识别这些外观。因此,系数永远不应该设置为零,而是对所有系数进行加权求和,其权重由聚类为非铣削纹理的系数图像的平均 L2 范数自适应计算。中值绝对偏差 (MAD) 是在未分类为表示铣削纹理的所有图像 Gl(如图 3 所示的系数图像)上计算的:M AD(Gl(x, y))) = 中值(|中位数(Gl))−Gl(x, y)|)。标准偏差为 σ = M AD0.675。最终加权图像Gw的阈值选择为t =中位数(Gl)+k·σ,其中k > 1。使用这种方法,面向整体铣削纹理的微裂纹分割结果如图5所示。请注意,即使是这种微裂纹的精细细节也明显与铣削纹理分离。


图 5:使用剪切波分解分割微裂纹。由于裂纹的线状性质,它们与背景铣削纹理的相似性本身就很高。因此,所有系数的加权和,如 5b 所示,对于它们在 5c 中的最终可检测性至关重要。
C.傅里叶空间中的楔形滤波器
模式的2D傅里叶谱揭示了一个大幅度的楔形区域(见图2b),它与空间铣削纹理线条的方向正交。楔形主要代表铣削槽对应的较高频率。楔形的参数可以通过沿从光谱中心辐射为铅笔的虚直线采样平均幅度来估计。通过对平均幅度[1]应用kmeans聚类,可以找到定义楔形区域的开始和结束旋转角度。最后,可以对傅立叶谱应用掩码,该谱将楔形内的值设置为零,以便投射较低的频率。在傅里叶反变换之后,可以使用马氏距离分割铣削图案的周期部分和被认为是不规则缺陷。在这里,我们只自适应地参数化铣削纹理的全局楔形模型。然而,由于傅立叶分析中频谱的全局性质,我们省略了局部细化。因此,由于铣削纹理的近正则性引起的小扰动不包括在模型中,因此铣削纹理的二值化会产生伪影(即异常的假阳性分类),但也会产生假阴性,因为极端局部异常的傅里叶信号变为与铣削纹理的变化纠缠在一起。由于沿对角线轴的傅里叶变换遵循复杂度可以近似为 O(√N + N log2 N )。
D.纯相位变换
仅相位变换 (PHOT) [20] 对 2D 傅里叶域中的幅度进行归一化,从而消除所有规律。图像I(x, y)的归一化二维傅里叶谱F(u, v)计算为
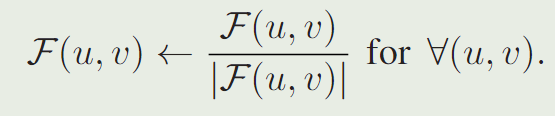
然后,应用逆变换得到 ^I(x, y) =F−1(u, v)。由于傅里叶谱的大小被丢弃,因此仅使用包含图像重要部分的相位信息。PHOT检测已经很好地符合我们的表面模型的图案区域的小缺陷和边界。此外,我们将标准 PHOT 与多尺度扩展 MPHOT [21] 进行比较,后者使用应用于纹理高斯金字塔的 PHOT 滤波器的融合。这允许精确分割更大的缺陷。数值复杂度由系数归一化的傅里叶变换定义:O(N 2 log2 N )。
E.基于模板的自相关