代码随想录算法训练营动态规划part17

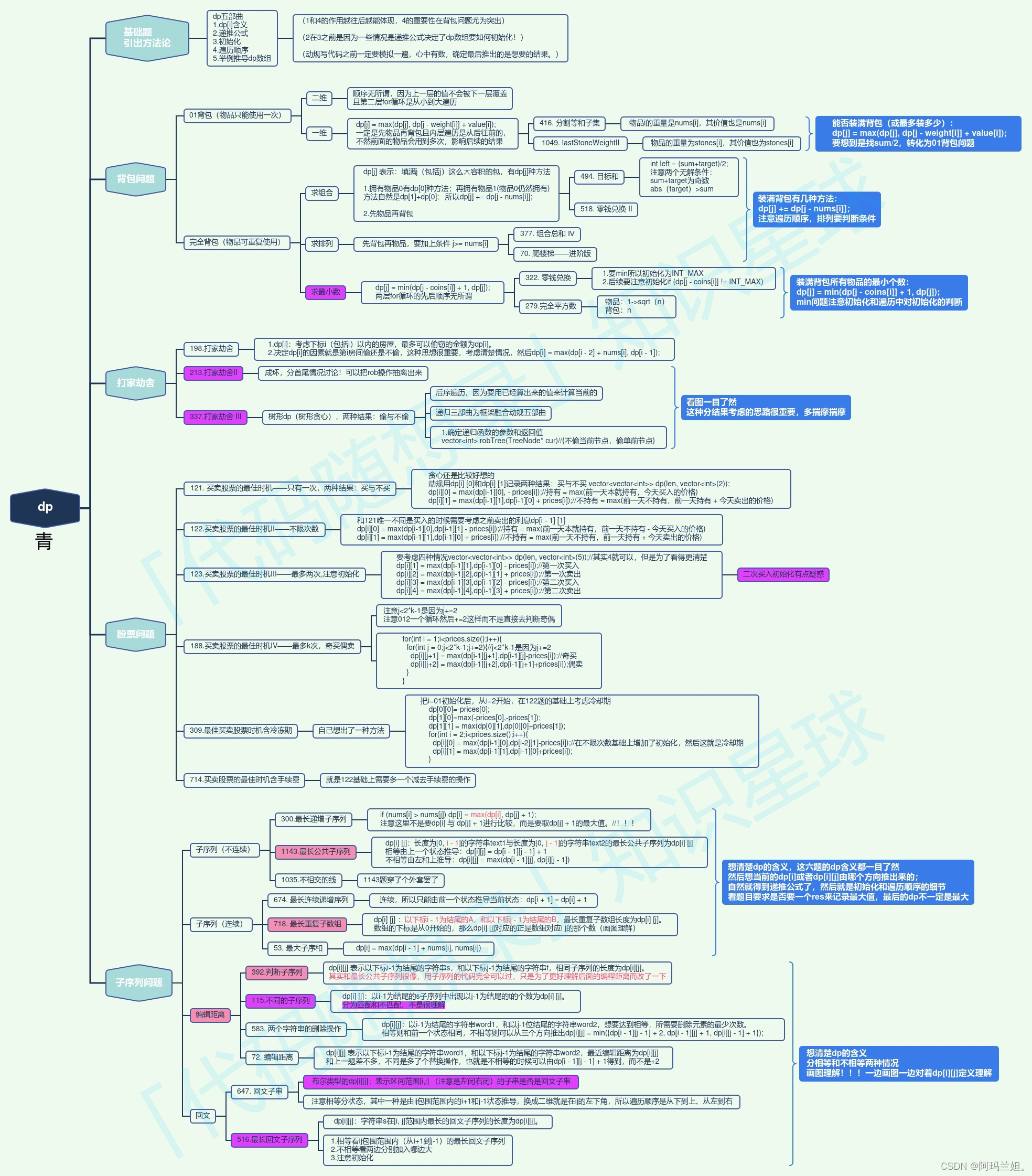
一、回文子串

647. 回文子串 - 力扣（LeetCode）

class Solution {public int countSubstrings(String s) {boolean[][] dp = new boolean[s.length()][s.length()];int ans = 0;for (int j = 0; j < s.length(); j++) {for (int i = 0; i <= j; i++) {if (s.charAt(i) == s.charAt(j) && (j - i < 2 || dp[i + 1][j - 1])) {dp[i][j] = true;ans++;}}}return ans;}
}

二、最长回文子序列

516. 最长回文子序列 - 力扣（LeetCode）

用 dp[i][j] 表示字符串 s 的下标范围 [i,j]内的最长回文子序列的长度。假设字符串 s 的长度为 n，则只有当 0≤i≤j<n 时，才会有 dp[i][j]>0，否则 dp[i][j]=0。

由于任何长度为 1 的子序列都是回文子序列，因此动态规划的边界情况是，对任意 0≤i<n，都有 dp[i][i]=1。

当 i<j 时，计算 dp[i][j] 需要分别考虑 s[i] 和 s[j] 相等和不相等的情况：

如果 s[i]=s[j]，则首先得到 s 的下标范围 [i+1,j−1] 内的最长回文子序列，然后在该子序列的首尾分别添加 s[i] 和 s[j]，即可得到 s 的下标范围 [i,j] 内的最长回文子序列，因此 dp[i][j]=dp[i+1][j−1]+2；

如果 s[i]≠s[j]，则 s[i] 和 s[j] 不可能同时作为同一个回文子序列的首尾，因此 dp[i][j]=max⁡(dp[i+1][j],dp[i][j−1])。

由于状态转移方程都是从长度较短的子序列向长度较长的子序列转移，因此需要注意动态规划的循环顺序。

最终得到 dp[0][n−1] 即为字符串 s 的最长回文子序列的长度。

class Solution {public int longestPalindromeSubseq(String s) {int n = s.length();int[][] dp = new int[n][n];for (int i = n - 1; i >= 0; i--) {dp[i][i] = 1;char c1 = s.charAt(i);for (int j = i + 1; j < n; j++) {char c2 = s.charAt(j);if (c1 == c2) {dp[i][j] = dp[i + 1][j - 1] + 2;} else {dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);}}}return dp[0][n - 1];}
}