题目
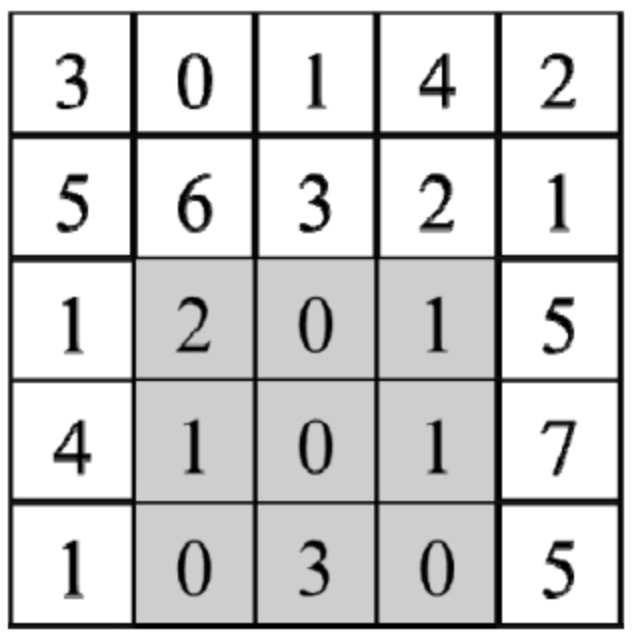
输入一个二维矩阵,如何计算给定左上角坐标和右下角坐标的子矩阵的数字之和?对于同一个二维矩阵,计算子矩阵的数字之和的函数可能由于输入不同的坐标而被反复调用多次。例如,输入图2.1中的二维矩阵,以及左上角坐标为(2,1)和右下角坐标为(4,3)的子矩阵,该函数输出8。
分析
如果不考虑时间复杂度,则采用蛮力法用两个嵌套的循环总是可以求出一个二维矩阵的数字之和。如果矩阵的行数和列数分别是m和n,那么这种蛮力法的时间复杂度是O(mn)。
只是这个题目提到,对于一个二维矩阵,可能由于输入不同的坐标而反复求不同子矩阵的数字之和,这说明应该优化求和的过程,要尽可能快地实现子矩阵的数字求和。
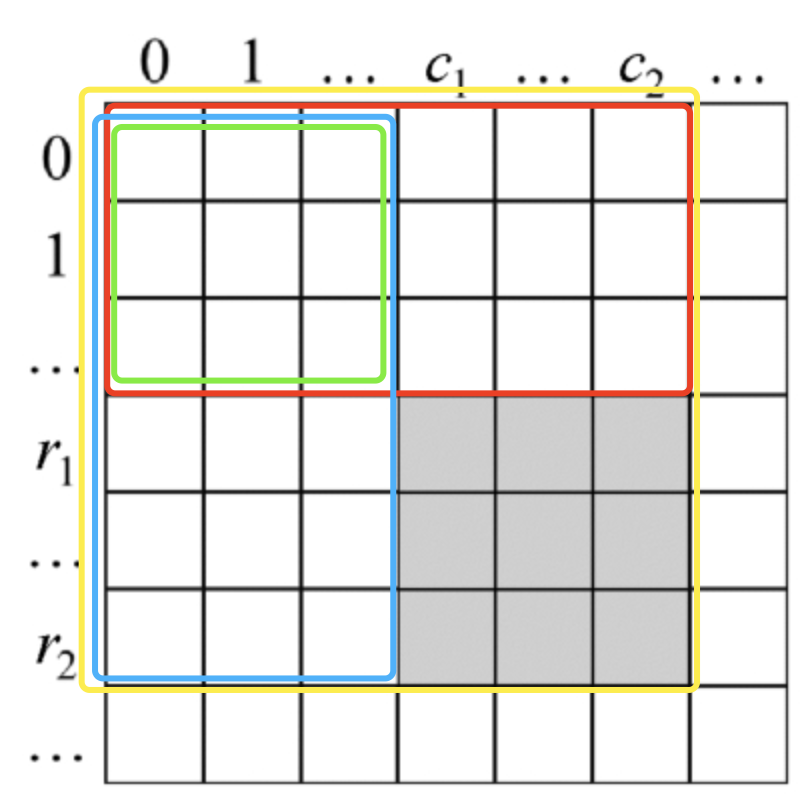
阴影面积 = 黄色正方形面积 + 绿色正方行面积 - 红色长方形面积 - 蓝色长方形面积
因此,可以在预处理阶段求出从左上角坐标为(0,0)到每个右下角坐标的子矩阵的数字之和。首先创建一个和输入矩阵大小相同的辅助矩阵sums,该矩阵中的坐标(i,j)的数值为输入矩阵中从左上角坐标(0,0)到右下角坐标(i,j)的子矩阵的数字之和。
下面分析如何生成辅助矩阵sums,即求得数组中的每个数字sums[i][j]。按照生成辅助矩阵sums的规则,sums[i][j]的值等于输入矩阵中从左上角坐标为(0,0)到右下角坐标为(i,j)的子矩阵的数字之和。可以把从左上角坐标为(0,0)到右下角坐标为(i,j)的子矩阵的数字看成由两部分组成。第1部分是从左上角坐标为(0,0)到右下角坐标为(i-1,j)的子矩阵,该子矩阵的数字之和等于sums[i-1][j]。第2部分是输入矩阵中第i行中列号从0到j的所有数字。如果按照从左到右的顺序计算sums[i][j],则可以逐个累加第i行的数字,从而得到子矩阵第2部分的数字之和。
解
public class Test {public static void main(String[] args) {int[][] nums = {{3, 0, 1, 4, 2},{5, 6, 3, 2, 1},{1, 2, 0, 1, 5},{4, 1, 0, 1, 7},{1, 0, 3, 0, 5}};sums = generateNumMatrix(nums);int result = sumRegion(2, 1, 4, 3);System.out.println(result);}private static int[][] sums;public static int[][] generateNumMatrix(int[][] matrix) {if (matrix.length == 0 || matrix[0].length == 0) {return null;}int[][] sums = new int[matrix.length + 1][matrix[0].length + 1];for (int i = 0; i < matrix.length; i++) {int rowSum = 0;for (int j = 0; j < matrix[0].length; j++) {rowSum += matrix[i][j];sums[i + 1][j + 1] = sums[i][j + 1] + rowSum;}}return sums;}public static int sumRegion(int row1, int col1, int row2, int col2) {//return sums[row2][col2] + sums[row1-1][col1-1] - sums[row1-1][col2] - sums[row2][col1-1];return sums[row2 + 1][col2 + 1] + sums[row1][col1] - sums[row1][col2 + 1] - sums[row2 + 1][col1];}
}
如果输入矩阵的行数和列数分别是m和n,那么辅助数组sums的行数和列数分别为m+1和n+1,这样只是为了简化代码逻辑。如果用公式sums[r2][c2]+sums[r1-1][c2]-sums[r2][c1-1]+sums[r1-1][c1-1]求解左上角坐标为(r1,c1)、右下角坐标为(r2,c2)的子矩阵的数字之和,由于坐标值r1或c1有可能等于0,因此r1-1或c1-1可能是负数,不再是有效的数组下标。如果在矩阵的最上面增加一行,最左面增加一列,这样就不必担心出现数组下标为-1的情形。