原始 Markdown文档、Visio流程图、XMind思维导图见:https://github.com/LiZhengXiao99/Navigation-Learning
文章目录
- 一、基础概念
- 1、坐标系定义
- 1. 惯性坐标系( i 系 )
- 2. 地心地固坐标系( e 系 )
- 3. 导航坐标系( n 系)
- 4. 载体坐标系( b 系 )
- 5. 地理坐标系( g 系)
- 6. 大地坐标系( LLA )
- 2、反对称阵
- 3、欧拉角
- 4、旋转矩阵/方向余弦阵
- 5、四元数
- 6、等效旋转矢量
- 二、PSINS中的表示转换
- 1、姿态阵/姿态四元数/欧拉角的表示 Cnb/qnb/att
- 2、四元数计算
- 1. 四元数共轭:qconj
- 2. 四元数归一化:qconj
- 3. 四元数相乘:qmual
- 4. 四元数乘向量(三维向量的坐标变换):qmulv
- 5. 四元数加失准角误差:qaddphi
- 6. 四元数减失准角误差:qdelphi
- 7. 由四元数和真实四元数计算失准角误差:qq2phi
- 3、各种姿态表示的转换
- 1. 欧拉角 -> 姿态阵:a2mat
- 2. 姿态阵 -> 欧拉角:m2att
- 3. 四元数 -> 姿态阵:q2mat
- 4. 姿态阵 -> 四元数:m2qua
- 5. 欧拉角 -> 四元数:a2qua
- 6. 四元数 -> 欧拉角:q2att
- 7. 四元数 -> 等效旋转矢量:q2rv
- 8. 等效旋转矢量 -> 四元数:rv2q
- 9. 姿态阵 -> 等效旋转矢量:m2rv
- 10. 等效旋转矢量 -> 姿态阵:rv2m
- 11. 反对称阵
- 11. 反对称阵
载体的姿态指的是载体坐标系(b系)和导航坐标系(n系)之间的方位关系,而两坐标系直接的方位关系可以等效成力学中的 刚体定点转动问题。在刚体定点转动理论中,描述动坐标系相对参考坐标系方位关系的传统方法有 欧拉角法、 方向余弦法、 四元数法。传统的方向余弦法和四元数法都是假设机体做定轴运动,在此种情况下没有 不可交换性误差。然而在捷联惯导系统中,惯性器件是直接安装在机体上,跟随机体的运动,所以假定机体运动为定轴不太符合实际环境,因此针对高动态境,还有更高精度的姿态解算方法: 等效旋转矢量法。
由于捷联惯导系统采用通过姿态矩阵计算建立的数学平台,在捷联惯导系统的姿态、速度和位置的更新算法中,姿态算法对整个系统的精度影响最大,它是算法研究和设计的核心。
姿态求解目标:知道初始姿态参数,实时根据陀螺仪的测量,输出姿态参数:

一、基础概念
1、坐标系定义
根据原点的位置和轴线得到指向,可以将惯导坐标系分为以下几类:
1. 惯性坐标系( i 系 )
也称 ECI,原点在地球质心,坐标轴不随地球自转(Z轴指向北极,X轴指向春分点)。惯性传感器输出以此为基准。尽管受到太阳引力场的作用,存在 6 ∗ 1 0 − 7 g 6*10^{-7}g 6∗10−7g 的公转向心力;但在地球表面以地球做惯导参考基准时,运动载体与地球处于近似相同的太阳引力场中,可以不考虑其影响。
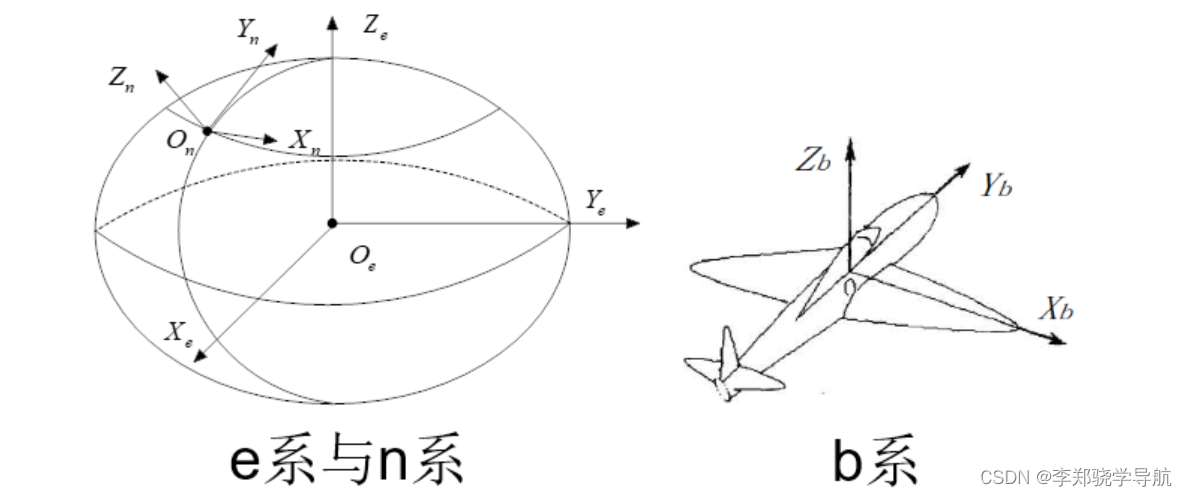
2. 地心地固坐标系( e 系 )
也称 ECEF,原点在地图质心,坐标轴随地球自转(Z轴指北极,X轴指向赤道和本初子午线交点)。GNSS 系统最常用此坐标系。ECEF 相对于 ECI 的角运动大小就是地球自转角速率 ω i e \omega_{ie} ωie。
3. 导航坐标系( n 系)
也称当地水平坐标系,原点在载体,坐标轴不随载体变化。有两种描述:北东地(NED)、东北天(ENU)。是惯导求解参数时所使用的坐标系,惯导解算对重力加速度特别在意,可以由此坐标系显现出来。
4. 载体坐标系( b 系 )
原点在载体,坐标轴随载体变化。与导航坐标系相对于,也有两种描述:前右下(FRD)、右前上(RFU)。一套导航系统中有很多个 b 系:IMU的 b 系、载体的 b 系、相机的 b 系等等。b 系和 i 系的方位关系可以用一组欧拉角来描述。
在 PSINS 中:导航坐标系(n):东E-北N-天U、载体坐标系(b):右R-前F-上U
5. 地理坐标系( g 系)
原点为与运载体的中心,x 轴指向地理东向,y 轴指地理北向,z 轴垂直与地理椭球指天;地理坐标系相对于地心地固坐标系的关系可以用纬经高来表示。
6. 大地坐标系( LLA )
也是地固坐标系。坐标原点位于地心,基于基准椭球体(基准椭球体是定义的与地球几何最吻合的椭球体)。大地纬度 ϕ \phi ϕ 是过该点的基准椭球面法线与赤道面的夹角。纬度值在-90°到+90°之间。北半球为正,南半球为负。大地经度 λ \lambda λ 是过该点的子午面与本初子午面之间的夹角。经度值在-180°到+180°之间。大地高度 h h h 是过该点到基准椭球面的法线距离,基准椭球面以内为负,以外为正。
2、反对称阵
( V × ) = [ 0 − V z V y V z 0 − V x − V y V x 0 ] (\boldsymbol{V} \times)=\left[\begin{array}{ccc} 0 & -V_{z} & V_{y} \\ V_{z} & 0 & -V_{x} \\ -V_{y} & V_{x} & 0 \end{array}\right] (V×)= 0Vz−Vy−Vz0VxVy−Vx0
反对称阵要点:
-
对角线上都为 0,上下两部分对称相反,即: ( V × ) = − ( V × ) T (V \times)=-(V\times)^{T} (V×)=−(V×)T ,所以称之为反对称阵。
-
一个向量叉乘另一个向量,等于点乘另一个向量的反对称阵,化叉乘为点乘。
-
反对称阵的幂方通式:
( V × ) i = { ( − 1 ) ( i − 1 ) / 2 v i − 1 ( V × ) i = 1 , 3 , 5 , ⋯ ( − 1 ) ( i − 2 ) / 2 v i − 2 ( V × ) 2 i = 2 , 4 , 6 , ⋯ (\boldsymbol{V} \times)^{i}=\left\{\begin{array}{ll} (-1)^{(i-1) / 2} v^{i-1}(\boldsymbol{V} \times) & i=1,3,5, \cdots \\ (-1)^{(i-2) / 2} v^{i-2}(\boldsymbol{V} \times)^{2} & i=2,4,6, \cdots \end{array}\right. (V×)i={(−1)(i−1)/2vi−1(V×)(−1)(i−2)/2vi−2(V×)2i=1,3,5,⋯i=2,4,6,⋯
3、欧拉角
A = [ θ γ ψ ] T \boldsymbol{A}=\left[\begin{array}{lll}\theta & \gamma & \psi\end{array}\right]^{\mathrm{T}} A=[θγψ]T
欧拉角是一种用绕坐标轴转换的角度描述两个坐标系之间相对姿态的经典方法,物理含义直观,易于理解,尤其是用于描述载体坐标系相对于当地导航坐标系的运动。
欧拉角表示转动:三维空间中,一个直角坐标系相对于另一个直角坐标系的方位关系,可通过三个依次转动来描述,每次旋转所绕的坐标轴与前后旋转轴正交。欧拉证明任意两个正交坐标系之间的相对朝向关系可以通过一组不少于 3 的角度来描述,这三次旋转的转角称为一组欧拉角(欧拉角组)。

欧拉角表示姿态:想描述载体的姿态,可以指定一个参考坐标系,然后用一组欧拉角来描述与载体与固联的坐标系相对于参考坐标系的转动。在地球附近的导航应用中,参考坐标系一般默认选择当地地理坐标系, 而动坐标系为与运载体固联的坐标系。

- 航向角:载体纵轴正方向在当地水平面上的投影与当地地理北向的夹角,常取北偏东为正,一般用 ψ 表示,角度范围为 0 ∼ 360◦ 或 −180◦ ∼ +180◦。
- 俯仰角:载体纵轴正方向与其水平投影线之间的夹角,当载体“抬头”时定义为正,一般用 θ 表示,取值范围为 −90◦ ∼ 90◦。
- 横滚角:载体立轴正方向与载体纵轴所在铅垂面之间的夹角,当载体向右倾斜(如飞机右机翼下压)时为正,用 ϕ \phi ϕ 表示,取值范围为 −180◦ ∼ +180◦。
欧拉角要点:
- 两个正交坐标系之间的相对朝向关系可以通过一组欧拉角组来描述, 给定一组欧拉角须同时指定对应的转轴顺序。PSINS中用的是东北天、312 欧拉角
- 导航姿态角, 包括航向角、俯仰角和横滚角, 与载体的物理轴向紧密关联, 而与选择的载体数学坐标系无关。
- 当俯仰角为 ± 9 0 ∘ \pm 90^{\circ} ±90∘ 时, 欧拉角变换存在奇异值, 此时无法区分横滚角和航向角。因此,欧拉角法不能用于全姿态导航应用。
- 欧拉角组不能直接相加来表示两次转动的合成。
4、旋转矩阵/方向余弦阵
C = [ c x x c x y c x z c y x c y y c y z c z x c z y c z z ] \boldsymbol{C}=\left[\begin{array}{lll}c_{x x} & c_{x y} & c_{x z} \\ c_{y x} & c_{y y} & c_{y z} \\ c_{z x} & c_{z y} & c_{z z}\end{array}\right] C= cxxcyxczxcxycyyczycxzcyzczz
方向余弦矩阵(Direction Cosine Matrix, DCM)用向量的方向余弦来表示的姿态矩阵,常用于描述两个坐标系的相对姿态。相比于欧拉角,方向余弦矩阵显得抽象许多,但它处理向量的投影变换非常方便。
我们知道,空间中的矢量的三个投影值就是坐标,同一个矢量在 i i i 系和 b b b 系有两套坐标,它们的关系可以表示为:
V = V x i i i + V y i j i + V z i k i = V x b i b + V y b j b + V z b k b \boldsymbol{V}=V_{x}^{i} \boldsymbol{i}_{i}+V_{y}^{i} \boldsymbol{j}_{i}+V_{z}^{i} \boldsymbol{k}_{i}=V_{x}^{b} \boldsymbol{i}_{b}+V_{y}^{b} \boldsymbol{j}_{b}+V_{z}^{b} \boldsymbol{k}_{b} V=Vxiii+Vyiji+Vziki=Vxbib+Vybjb+Vzbkb
即 [ i i j i k i ] [ V x i V y i V z i ] = [ i b j b k b ] [ V x b V y b V z b ] = [ i i j i k i ] P [ V x b V y b V z b ] \left[\begin{array}{lll}\boldsymbol{i}_{i} & \boldsymbol{j}_{i} & \boldsymbol{k}_{i}\end{array}\right]\left[\begin{array}{c}V_{x}^{i} \\ V_{y}^{i} \\ V_{z}^{i}\end{array}\right]=\left[\begin{array}{lll}\boldsymbol{i}_{b} & \boldsymbol{j}_{b} & \boldsymbol{k}_{b}\end{array}\right]\left[\begin{array}{c}V_{x}^{b} \\ V_{y}^{b} \\ V_{z}^{b}\end{array}\right]=\left[\begin{array}{lll}\boldsymbol{i}_{i} & \boldsymbol{j}_{i} & \boldsymbol{k}_{i}\end{array}\right] \boldsymbol{P}\left[\begin{array}{c}V_{x}^{b} \\ V_{y}^{b} \\ V_{z}^{b}\end{array}\right] [iijiki] VxiVyiVzi =[ibjbkb] VxbVybVzb =[iijiki]P VxbVybVzb
有:
[ V x i V y i V z i ] = P [ V x b V y b V z b ] \left[\begin{array}{c}V_{x}^{i} \\ V_{y}^{i} \\ V_{z}^{i}\end{array}\right]=\boldsymbol{P}\left[\begin{array}{c}V_{x}^{b} \\ V_{y}^{b} \\ V_{z}^{b}\end{array}\right] VxiVyiVzi =P VxbVybVzb
记为 V i = P V b = C b i V b \boldsymbol{V}^{i}=\boldsymbol{P} \boldsymbol{V}^{b}=\boldsymbol{C}_{b}^{i} \boldsymbol{V}^{b} Vi=PVb=CbiVb, C b i C_b^i Cbi 称为坐标系变换矩阵 (i->b) 或 坐标变换矩阵 (b->i),也称之为方向余弦阵、过渡矩阵。
方向余弦阵要点:
- 由于都是单位阵,方向余弦阵中每一个元素都表示两套坐标系坐标轴夹角的余弦值,以此得名。
- 区分清坐标系变换矩阵和坐标变换矩阵。
- 方向余弦阵虽然有 9 个参数,但其中包含了 6 个约束条件,即行向量模为 1 且两两正交,只有 3 个参数是独立的。
- 方向余弦矩阵是正交矩阵, ( C α β ) − 1 = ( C α β ) T \left(\mathbf{C}_{\alpha}^{\beta}\right)^{-1}=\left(\mathbf{C}_{\alpha}^{\beta}\right)^{\mathrm{T}} (Cαβ)−1=(Cαβ)T 。多次连续转动可以用相应的多个方向余弦矩阵连乘来表示: C a d = C b d C a b \mathbf{C}_{a}^{d}=\mathbf{C}_{b}^{d} \mathbf{C}_{a}^{b} Cad=CbdCab 。
- 当载体运动时,两个坐标系之间的相对姿态随时间变化,对应的方向余弦矩阵 C b R ( t ) \mathbf{C}_{b}^{R}(t) CbR(t) 则是 一个时变矩阵, 其微分方程为 C ˙ b R = C b R ( ω R b b × ) \dot{\mathrm{C}}_{b}^{R}=\mathbf{C}_{b}^{R}\left(\boldsymbol{\omega}_{R b}^{b} \times\right) C˙bR=CbR(ωRbb×) 。
- 可用毕卡迭代法求解方向余弦矩阵的微分方程,得到一个以无限重积分表示的级数,也被称为毕卡级数,上述级数是收玫的,但只有在 “定轴转动” 这一特殊情形下才能得到如下形式的闭合解: C b R ( t ) = C ( 0 ) exp ( ∫ 0 t Ω ( τ ) d τ ) \mathbf{C}_{b}^{R}(t)=\mathbf{C}(0) \exp \left(\int_{0}^{t} \boldsymbol{\Omega}(\tau) d \tau\right) CbR(t)=C(0)exp(∫0tΩ(τ)dτ) 。
- 姿态更新公式: C b ( k ) i = C b ( k − 1 ) i C b ( k ) b ( k − 1 ) \mathbf{C}_{b(k)}^{i}=\mathbf{C}_{b(k-1)}^{i} \mathbf{C}_{b(k)}^{b(k-1)} Cb(k)i=Cb(k−1)iCb(k)b(k−1), C b ( k ) b ( k − 1 ) = I + sin Δ θ k Δ θ k [ Δ θ k × ] + 1 − cos Δ θ k Δ θ k 2 [ Δ θ k × ] 2 \mathbf{C}_{b(k)}^{b(k-1)}=\mathbf{I}+\frac{\sin \Delta \theta_{k}}{\Delta \theta_{k}}\left[\Delta \boldsymbol{\theta}_{k} \times\right]+\frac{1-\cos \Delta \theta_{k}}{\Delta \theta_{k}^{2}}\left[\Delta \boldsymbol{\theta}_{k} \times\right]^{2} Cb(k)b(k−1)=I+ΔθksinΔθk[Δθk×]+Δθk21−cosΔθk[Δθk×]2
- 对于普通惯性导航应用来说, b b b 系定轴转动这一假设一般都不成立的, 当该条件不满足时, 仍然将陀螺输出的角增量套用到式中进行姿态更新的递推计算, 则会带来姿态更新求解的不可交换性误差,可用等效旋转矢量来解决这个问题。
5、四元数
Q = q 0 + q 1 i + q 2 j + q 3 k = q 0 + q v \boldsymbol{Q}=q_{0}+q_{1} \boldsymbol{i}+q_{2} \boldsymbol{j}+q_{3} \boldsymbol{k}=q_{0}+\boldsymbol{q}_{v} Q=q0+q1i+q2j+q3k=q0+qv
我们知道复数可以看成是复平面上的向量,即一个二维的向量,将复数的概念再拓展可以得到四元数,用以描述三维空间中的向量。
四元数要点:
-
四元数主要有以下表示方式: q = q 0 + q 1 i + q 2 j + q 3 k \boldsymbol{q}=q_{0}+q_{1} \boldsymbol{i}+q_{2} \boldsymbol{j}+q_{3} \boldsymbol{k} q=q0+q1i+q2j+q3k 、向量坐标形式 q = [ q 0 , q 1 , q 2 , q 3 ] T \boldsymbol{q}=\left[q_{0}, q_{1}, q_{2}, q_{3}\right]^{\mathrm{T}} q=[q0,q1,q2,q3]T 、 q = q s + q v \boldsymbol{q}=q_{s}+\boldsymbol{q}_{v} q=qs+qv 或三角函数形式 q = cos θ 2 + u sin θ 2 \boldsymbol{q}=\cos \frac{\theta}{2}+\boldsymbol{u} \sin \frac{\theta}{2} q=cos2θ+usin2θ (与等效旋转矢量有关,做了归一化,模值为一)
-
四元数虚数单位之间的乘法有如下特点: 单位与单位自己相乘时, 表现与复数一样, 而两两之间的乘法则与三维向量的外积 (叉乘) 一样。
{ i ∘ i = j ∘ j = k ∘ k = − 1 i ∘ j = k , j ∘ k = i , k ∘ i = j , j ∘ i = − k , k ∘ j = − i , i ∘ k = − j \left\{\begin{array}{l}\boldsymbol{i} \circ \boldsymbol{i}=\boldsymbol{j} \circ \boldsymbol{j}=\boldsymbol{k} \circ \boldsymbol{k}=-1 \\ \boldsymbol{i} \circ \boldsymbol{j}=\boldsymbol{k}, \quad \boldsymbol{j} \circ \boldsymbol{k}=\boldsymbol{i}, \quad \boldsymbol{k} \circ \boldsymbol{i}=\boldsymbol{j}, \quad \boldsymbol{j} \circ \boldsymbol{i}=-k, \quad k \circ \boldsymbol{j}=-i, \quad \boldsymbol{i} \circ \boldsymbol{k}=-\boldsymbol{j}\end{array}\right. {i∘i=j∘j=k∘k=−1i∘j=k,j∘k=i,k∘i=j,j∘i=−k,k∘j=−i,i∘k=−j -
用四元数的旋转变换算子可实现三维向量的坐标变换: v R = q b R ∘ v b ∘ q b R ∗ \boldsymbol{v}^{R}=\boldsymbol{q}_{b}^{R} \circ \boldsymbol{v}^{b} \circ \boldsymbol{q}_{b}^{R^{*}} vR=qbR∘vb∘qbR∗ 。
-
单位四元数三角表示法: Q = q 0 + q v = cos ϕ 2 + u sin ϕ 2 \boldsymbol{Q}=q_{0}+\boldsymbol{q}_{v}=\cos \frac{\phi}{2}+\boldsymbol{u} \sin \frac{\phi}{2} Q=q0+qv=cos2ϕ+usin2ϕ 具有很清晰的物理意义。常在四元数的右边加上角标,写成 Q b i \boldsymbol{Q}_{b}^{i} Qbi,中 u \boldsymbol{u} u 表示动坐标系 ( b b b 系) 相对于参考坐标系 ( i i i 系) 旋转的单位转轴, ϕ \phi ϕ 表示旋转角度大小, ϕ u \phi \boldsymbol{u} ϕu 表示等效旋转矢量。使用角标后,共轭四元数可记为 Q i b = ( Q b i ) ∗ \boldsymbol{Q}_{i}^{b}=\left(\boldsymbol{Q}_{b}^{i}\right)^{*} Qib=(Qbi)∗,这与矩阵转置的表示方法类似,比如 C i b = ( C b i ) T \boldsymbol{C}_{i}^{b}=\left(\boldsymbol{C}_{b}^{i}\right)^{\mathrm{T}} Cib=(Cbi)T 。
-
四元数的微分方程式: q ˙ b R = 1 2 q b R ∘ [ 0 ω R b b ] \dot{\boldsymbol{q}}_{b}^{R}=\frac{1}{2} \boldsymbol{q}_{b}^{R} \circ\left[\begin{array}{c}0 \\ \boldsymbol{\omega}_{R b}^{b}\end{array}\right] q˙bR=21qbR∘[0ωRbb], 或写作矩阵形式: q ˙ b R = 1 2 W q b R \dot{\boldsymbol{q}}_{b}^{R}=\frac{1}{2} \mathbf{W} \boldsymbol{q}_{b}^{R} q˙bR=21WqbR 。由此建立了四元数与旋转角速度之间的关系。
-
求解四元数的微分方程, 当 b b b 系满足 “定轴转动” 条件时, 可得解析解: q b R ( t ) = \boldsymbol{q}_{b}^{R}(t)= qbR(t)= [ I cos Δ θ 2 + Θ Δ θ sin Δ θ 2 ] q b R ( 0 ) \left[\mathbf{I} \cos \frac{\Delta \theta}{2}+\frac{\Theta}{\Delta \theta} \sin \frac{\Delta \theta}{2}\right] \boldsymbol{q}_{b}^{R}(0) [Icos2Δθ+ΔθΘsin2Δθ]qbR(0) 。
-
还有八元数,用于描述螺旋运动,有线运动、角运动。
6、等效旋转矢量
欧拉在研究刚体运动时最早提出了等效旋转矢量的概念,他指出刚体的定点有限旋转都可以用绕经过该固定点的一个轴的一次转动来等效实现。并建立了刚体上单位矢量在转动前后的变换公式。现代捷联惯性导航姿态更新算法研究的关键在于如何使用陀螺的测量值构造出对应的等效旋转矢量,以尽量减小或消除姿态更新算法中的不可交换性误差。后续使用等效旋转矢量来计算姿态的变化,如用方向余弦矩阵或四元数来表示,将变得非常简单。
用几个角增量的采样值,根据各种子样算法,算一个等效旋转矢量,再用算出的等效旋转矢量更新方向余弦阵、四元数。

空间矢量 r r r 绕转轴矢量 u u u 转动 ϕ \phi ϕ ,转动得到的矢量 r ′ r^{'} r′ 。四个量直接一定有函数关系 r ′ = f ( r , u , ϕ ) r^{'}=f(r,u,\phi) r′=f(r,u,ϕ) ,利用一些几何关系,可以推导得到:
r ′ = ( u ⋅ r ) u + ( u × r ) × u cos ϕ + u × r sin ϕ = [ I + ( u × ) 2 ] r − ( u × ) 2 r cos ϕ + u × r sin ϕ = [ I + sin ϕ ( u × ) + ( 1 − cos ϕ ) ( u × ) 2 ] r = D r \begin{aligned} \boldsymbol{r}^{\prime} & =(\boldsymbol{u} \cdot \boldsymbol{r}) \boldsymbol{u}+(\boldsymbol{u} \times \boldsymbol{r}) \times \boldsymbol{u} \cos \phi+\boldsymbol{u} \times \boldsymbol{r} \sin \phi \\ & =\left[\boldsymbol{I}+(\boldsymbol{u} \times)^{2}\right] \boldsymbol{r}-(\boldsymbol{u} \times)^{2} \boldsymbol{r} \cos \phi+\boldsymbol{u} \times \boldsymbol{r} \sin \phi \\ & =\left[\boldsymbol{I}+\sin \phi(\boldsymbol{u} \times)+(1-\cos \phi)(\boldsymbol{u} \times)^{2}\right] \boldsymbol{r}=\boldsymbol{D} \boldsymbol{r}\end{aligned} r′=(u⋅r)u+(u×r)×ucosϕ+u×rsinϕ=[I+(u×)2]r−(u×)2rcosϕ+u×rsinϕ=[I+sinϕ(u×)+(1−cosϕ)(u×)2]r=Dr
可记 D = I + sin ϕ ( u × ) + ( 1 − cos ϕ ) ( u × ) 2 \boldsymbol{D}=\boldsymbol{I}+\sin \phi(\boldsymbol{u} \times)+(1-\cos \phi)(\boldsymbol{u} \times)^{2} D=I+sinϕ(u×)+(1−cosϕ)(u×)2 ,此公式称为罗德里格旋转公式; r ′ r' r′ 转到 r r r 中间乘的矩阵称为罗德里格旋转矩阵,和转轴 u u u 及转角 ϕ \phi ϕ 有关。
将罗德里格旋转公式用于直角坐标系的单位坐标轴,可将参考坐标系转到动坐标系:
i b = D i i j b = D j i k b = D k i } \left.\begin{array}{c}\boldsymbol{i}_{b}=\boldsymbol{D} \boldsymbol{i}_{i} \\ \boldsymbol{j}_{b}=\boldsymbol{D} \boldsymbol{j}_{i} \\ \boldsymbol{k}_{b}=\boldsymbol{D} \boldsymbol{k}_{i}\end{array}\right\} ib=Diijb=Djikb=Dki⎭ ⎬ ⎫
{ 基旋转变换关系: [ i b j b k b ] = D [ i i j i k i ] 基投影变换关系: [ i b j b k b ] = [ i i j i k i ] P \left\{\begin{array}{c} 基旋转变换关系:\left[\begin{array}{lll}\boldsymbol{i}_{b} & \boldsymbol{j}_{b} & \boldsymbol{k}_{b}\end{array}\right]=\boldsymbol{D}\left[\begin{array}{lll}\boldsymbol{i}_{i} & \boldsymbol{j}_{i} & \boldsymbol{k}_{i}\end{array}\right] \\ 基投影变换关系:{\left[\begin{array}{lll}\boldsymbol{i}_{b} & \boldsymbol{j}_{b} & \boldsymbol{k}_{b}\end{array}\right]=\left[\begin{array}{lll}\boldsymbol{i}_{i} & \boldsymbol{j}_{i} & \boldsymbol{k}_{i}\end{array}\right] \boldsymbol{P}} \\ \end{array}\right. {基旋转变换关系:[ibjbkb]=D[iijiki]基投影变换关系:[ibjbkb]=[iijiki]P
在 i 系投影: [ i b i j b i k b i ] = D [ i i i j i i k i i ] = D I [ i b i j b i k b i ] = [ i i i j i i k i i ] P = I P } D = P = C b i 在 i 系投影:\left.\begin{array}{l}{\left[\begin{array}{lll}\boldsymbol{i}_{b}^{i} & \boldsymbol{j}_{b}^{i} & \boldsymbol{k}_{b}^{i}\end{array}\right]=\boldsymbol{D}\left[\begin{array}{lll}\boldsymbol{i}_{i}^{i} & \boldsymbol{j}_{i}^{i} & \boldsymbol{k}_{i}^{i}\end{array}\right]=\boldsymbol{D} \boldsymbol{I}} \\ {\left[\begin{array}{lll}\boldsymbol{i}_{b}^{i} & \boldsymbol{j}_{b}^{i} & \boldsymbol{k}_{b}^{i}\end{array}\right]=\left[\begin{array}{lll}\boldsymbol{i}_{i}^{i} & \boldsymbol{j}_{i}^{i} & \boldsymbol{k}_{i}^{i}\end{array}\right] \boldsymbol{P}=\boldsymbol{I P}}\end{array}\right\} \quad \boldsymbol{D}=\boldsymbol{P}=\boldsymbol{C}_{b}^{i} 在i系投影:[ibijbikbi]=D[iiijiikii]=DI[ibijbikbi]=[iiijiikii]P=IP}D=P=Cbi
P = D P=D P=D 表明,罗德里格旋转矩阵 D D D 正好是从参考坐标系( i i i 系)到动坐标系( b b b 系)的过渡矩阵,它也是从 b b b 系到 i i i 系的坐标变换矩阵。因此可以将罗德里格旋转公式重新写为方向阵的形式:
C b i = I + sin ϕ ( u × ) + ( 1 − cos ϕ ) ( u × ) 2 \boldsymbol{C}_{b}^{i}=\boldsymbol{I}+\sin \phi(\boldsymbol{u} \times)+(1-\cos \phi)(\boldsymbol{u} \times)^{2} Cbi=I+sinϕ(u×)+(1−cosϕ)(u×)2
进一步, 若记 ϕ = ϕ u \boldsymbol{\phi}=\phi \boldsymbol{u} ϕ=ϕu 和 ϕ = ∣ ϕ ∣ \phi=|\boldsymbol{\phi}| ϕ=∣ϕ∣, 则有 u = ϕ / ϕ \boldsymbol{u}=\boldsymbol{\phi} / {\phi} u=ϕ/ϕ ,得:
C b i = I + sin ϕ ϕ ( ϕ × ) + 1 − cos ϕ ϕ 2 ( ϕ × ) 2 \boldsymbol{C}_{b}^{i}=\boldsymbol{I}+\frac{\sin \phi}{\phi}(\boldsymbol{\phi} \times)+\frac{1-\cos \phi}{\phi^{2}}(\boldsymbol{\phi} \times)^{2} Cbi=I+ϕsinϕ(ϕ×)+ϕ21−cosϕ(ϕ×)2
这里 ϕ \boldsymbol{\phi} ϕ 称为等效旋转矢量(RV,简称旋转矢量)
等效旋转矢量要点:
- 刚体的有限转动是不可交换的。刚体的定点有限旋转都可以用绕经过该固定点的一个轴的一次转动来实现。
- 其矢量方向表示旋转的方向,模的大小表示旋转角度大小。
- 当载体的角速度方向随时间变化而不是做 “定轴转动” 时, 直接将传感器角增量测量值代 入方向余弦矩阵或四元数微分方程的求解计算式中,则会带来 “不可交换性误差”。
- Bortz 方程: ϕ ˙ = ω + 1 2 ( ϕ × ω ) + 1 ϕ 2 [ 1 − ϕ sin ϕ 2 ( 1 − cos ϕ ) ] ϕ × ( ϕ × ω ) \dot{\phi}=\boldsymbol{\omega}+\frac{1}{2}(\phi \times \omega)+\frac{1}{\phi^{2}}\left[1-\frac{\phi \sin \phi}{2(1-\cos \phi)}\right] \boldsymbol{\phi} \times(\boldsymbol{\phi} \times \boldsymbol{\omega}) ϕ˙=ω+21(ϕ×ω)+ϕ21[1−2(1−cosϕ)ϕsinϕ]ϕ×(ϕ×ω) 。是一种常用的等效旋转矢量微分方程,利用等效旋转矢量进行转动不可交换误差补偿。
- 等效旋转矢量的双子样求解式: ϕ k = Δ θ k + 1 12 Δ θ k − 1 × Δ θ k \phi_{k}=\Delta \theta_{k}+\frac{1}{12} \Delta \theta_{k-1} \times \Delta \theta_{k} ϕk=Δθk+121Δθk−1×Δθk 。
二、PSINS中的表示转换
1、姿态阵/姿态四元数/欧拉角的表示 Cnb/qnb/att
-
有角标的符号书写一般遵从规律是从左到右从上到下。
-
姿态阵:
Cnb,表示从 b 系到 n 系的坐标变换矩阵。对应姿态四元数写为qnb。 -
欧拉角:
att=[俯仰pitch; 横滚roll; 方位yaw]。没有按照转到顺序来写,如果按转动顺序,东北天坐标系转到右前下坐标系,常见先转方位角、然后俯仰角、横滚角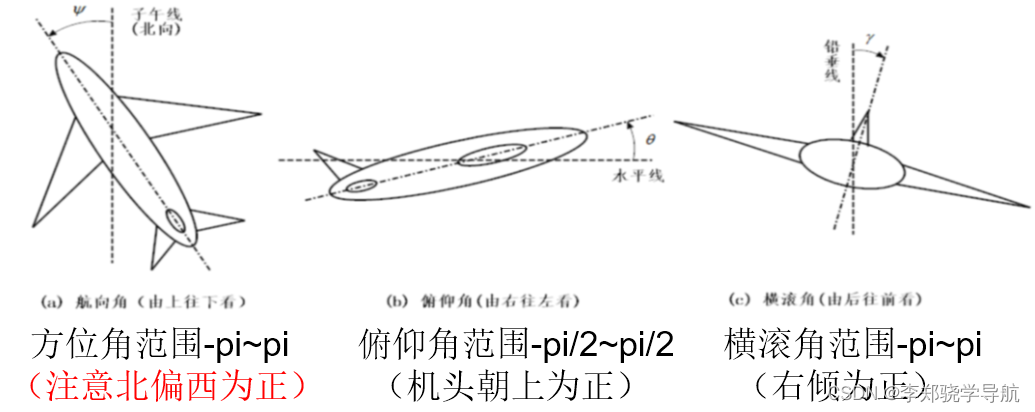
2、四元数计算
1. 四元数共轭:qconj
function qo = qconj(qi)qo = [qi(1); -qi(2:4)];
2. 四元数归一化:qconj
function qnb = qnormlz(qnb)qnb = qnb/norm(qnb);
3. 四元数相乘:qmual
{ i ∘ i = j ∘ j = k ∘ k = − 1 i ∘ j = k , j ∘ k = i , k ∘ i = j , j ∘ i = − k , k ∘ j = − i , i ∘ k = − j \left\{\begin{array}{l}\boldsymbol{i} \circ \boldsymbol{i}=\boldsymbol{j} \circ \boldsymbol{j}=\boldsymbol{k} \circ \boldsymbol{k}=-1 \\ \boldsymbol{i} \circ \boldsymbol{j}=\boldsymbol{k}, \quad \boldsymbol{j} \circ \boldsymbol{k}=\boldsymbol{i}, \quad \boldsymbol{k} \circ \boldsymbol{i}=\boldsymbol{j}, \quad \boldsymbol{j} \circ \boldsymbol{i}=-k, \quad k \circ \boldsymbol{j}=-i, \quad \boldsymbol{i} \circ \boldsymbol{k}=-\boldsymbol{j}\end{array}\right. {i∘i=j∘j=k∘k=−1i∘j=k,j∘k=i,k∘i=j,j∘i=−k,k∘j=−i,i∘k=−j
不满足交换率。 i 、 j 、 k i、j、k i、j、k 正向相乘等于后面一项,反向相乘要加负号。

function q = qmul(q1, q2)if length(q2)==3, q2=[0; q2]; end % 0-scale quaternionq = [ q1(1) * q2(1) - q1(2) * q2(2) - q1(3) * q2(3) - q1(4) * q2(4);q1(1) * q2(2) + q1(2) * q2(1) + q1(3) * q2(4) - q1(4) * q2(3);q1(1) * q2(3) + q1(3) * q2(1) + q1(4) * q2(2) - q1(2) * q2(4);q1(1) * q2(4) + q1(4) * q2(1) + q1(2) * q2(3) - q1(3) * q2(2) ];
4. 四元数乘向量(三维向量的坐标变换):qmulv
function vo = qmulv(q, vi)qo1 = - q(2) * vi(1) - q(3) * vi(2) - q(4) * vi(3);qo2 = q(1) * vi(1) + q(3) * vi(3) - q(4) * vi(2);qo3 = q(1) * vi(2) + q(4) * vi(1) - q(2) * vi(3);qo4 = q(1) * vi(3) + q(2) * vi(2) - q(3) * vi(1);vo = vi;vo(1) = -qo1 * q(2) + qo2 * q(1) - qo3 * q(4) + qo4 * q(3);vo(2) = -qo1 * q(3) + qo3 * q(1) - qo4 * q(2) + qo2 * q(4);vo(3) = -qo1 * q(4) + qo4 * q(1) - qo2 * q(3) + qo3 * q(2);
5. 四元数加失准角误差:qaddphi
从真实导航系 ( n n n 系) 到计算导航系 ( n ′ n^{\prime} n′ 系) 的失准角为 ϕ \boldsymbol{\phi} ϕ, 反之,从 n ′ n^{\prime} n′ 系到 n n n 系的失准角应为 − ϕ -\boldsymbol{\phi} −ϕ,若将 − ϕ -\phi −ϕ 视为等效旋转矢量,则与其对应的变换四元数为 Q n n ′ Q_{n}^{n^{\prime}} Qnn′ 。程序中, 变量 qpb、qnb、phi分别代表 Q b n ′ , Q b n Q_{b}^{n^{\prime}}, Q_{b}^{n} Qbn′,Qbn 和 ϕ \phi ϕ 。
function qpb = qaddphi(qnb, phi)qpb = qmul(rv2q(-phi),qnb);
6. 四元数减失准角误差:qdelphi
对应于公式 Q b n = Q n ′ n ∘ Q b ′ Q_{b}^{n}=Q_{n^{\prime}}^{n}{ }^{\circ} Q_{b}^{\prime} Qbn=Qn′n∘Qb′,其含义是:在计算姿态四元数中扣除失准角后,获得真实 (更精确的) 姿态四元数。
function qnb = qdelphi(qpb, phi)qnb = qmul(rv2q(phi), qpb);
7. 由四元数和真实四元数计算失准角误差:qq2phi
先根据公式 Q n ′ n = Q b n ∘ ( Q b n ′ ) ∗ Q_{n^{\prime}}^{n}=Q_{b}^{n} \circ\left(Q_{b}^{n^{\prime}}\right){ }^{*} Qn′n=Qbn∘(Qbn′)∗ 求得误差四元数 Q n ′ n Q_{n^{\prime}}^{n} Qn′n,再由 Q n ′ n Q_{n^{\prime}}^{n} Qn′n 求解失准角 ϕ \boldsymbol{\phi} ϕ 。
function phi = qq2phi(qpb, qnb)qnp = qmul(qnb, qconj(qpb));phi = q2rv(qnp);
3、各种姿态表示的转换
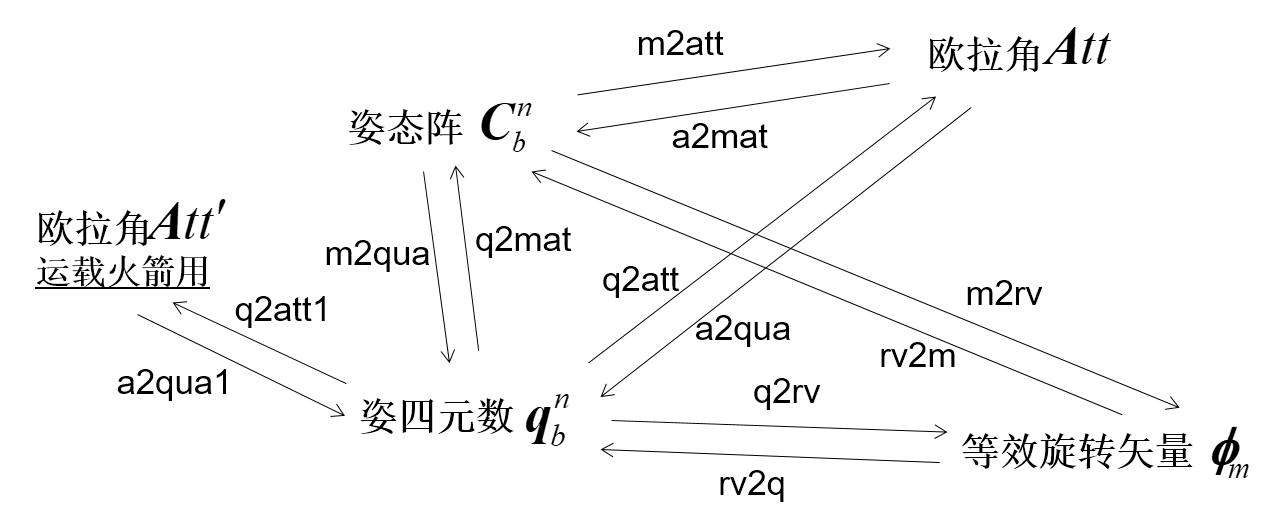
1. 欧拉角 -> 姿态阵:a2mat
欧拉角是用三次选择来表示姿态变化,将三次选择矩阵相乘得到方向余弦矩阵矩阵(姿态阵),其中转动顺序很关键。
C b t = C ψ C C C γ = [ c ψ − s ψ 0 s ψ ˙ c ψ 0 0 0 1 ] [ 1 0 0 0 c θ − s θ 0 s θ c θ ] [ c γ 0 s γ 0 1 0 − s γ 0 c γ ] = [ c ψ c γ − s ψ s θ s γ − s ψ c θ c ψ s γ + s ψ s θ c γ s ψ c γ + c ψ s θ s γ c ψ c θ s ψ s γ − c ψ s θ c γ − c θ s γ s θ c θ c γ ] = [ C 11 C 12 C 13 C 21 C 22 C 23 C 31 C 32 C 33 ] \begin{array}{l} \boldsymbol{C}_{b}^{t}= \boldsymbol{C}_{\psi} \boldsymbol{C}_{\boldsymbol{C}} \boldsymbol{C}_{\gamma}=\left[\begin{array}{ccc}c_{\psi} & -s_{\psi} & 0 \\ s_{\dot{\psi}} & c_{\psi} & 0 \\ 0 & 0 & 1\end{array}\right]\left[\begin{array}{ccc}1 & 0 & 0 \\ 0 & c_{\theta} & -s_{\theta} \\ 0 & s_{\theta} & c_{\theta}\end{array}\right]\left[\begin{array}{ccc}c_{\gamma} & 0 & s_{\gamma} \\ 0 & 1 & 0 \\ -s_{\gamma} & 0 & c_{\gamma}\end{array}\right]= \\ {\left[\begin{array}{ccc}c_{\psi} c_{\gamma}-s_{\psi} s_{\theta} s_{\gamma} & -s_{\psi} c_{\theta} & c_{\psi} s_{\gamma}+s_{\psi} s_{\theta} c_{\gamma} \\ s_{\psi} c_{\gamma}+c_{\psi} s_{\theta} s_{\gamma} & c_{\psi} c_{\theta} & s_{\psi} s_{\gamma}-c_{\psi} s_{\theta} c_{\gamma} \\ -c_{\theta} s_{\gamma} & s_{\theta} & c_{\theta} c_{\gamma}\end{array}\right]=\left[\begin{array}{ccc}C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33}\end{array}\right] }\end{array} Cbt=CψCCCγ= cψsψ˙0−sψcψ0001 1000cθsθ0−sθcθ cγ0−sγ010sγ0cγ = cψcγ−sψsθsγsψcγ+cψsθsγ−cθsγ−sψcθcψcθsθcψsγ+sψsθcγsψsγ−cψsθcγcθcγ = C11C21C31C12C22C32C13C23C33
function [Cnb, Cnbr] = a2mat(att)
% Convert Euler angles to direction cosine matrix(DCM).
% 欧拉角->姿态阵
% Prototype: [Cnb, Cnbr] = a2mat(att)
% Input: att - att=[pitch; roll; yaw] in radians
% Outputs: Cnb - DCM from navigation-frame(n) to body-frame(b), in yaw->pitch->roll
% (3-1-2) rotation sequence
% Cnbr - DCM in yaw->roll->pitch (3-2-1) rotation sequences = sin(att); c = cos(att);si = s(1); sj = s(2); sk = s(3); ci = c(1); cj = c(2); ck = c(3);Cnb = [ cj*ck-si*sj*sk, -ci*sk, sj*ck+si*cj*sk;cj*sk+si*sj*ck, ci*ck, sj*sk-si*cj*ck;-ci*sj, si, ci*cj ];if nargout==2 % dual Euler angle DCMCnbr = [ cj*ck, si*sj*ck-ci*sk, ci*sj*ck+si*sk;cj*sk, si*sj*sk+ci*ck, ci*sj*sk-si*ck;-sj, si*cj, ci*cj ];endfunction [Cnb, Cnbr] = a2mat(att)s = sin(att); c = cos(att);si = s(1); sj = s(2); sk = s(3); ci = c(1); cj = c(2); ck = c(3);Cnb = [ cj*ck-si*sj*sk, -ci*sk, sj*ck+si*cj*sk;cj*sk+si*sj*ck, ci*ck, sj*sk-si*cj*ck;-ci*sj, si, ci*cj ];if nargout==2 % dual Euler angle DCMCnbr = [ cj*ck, si*sj*ck-ci*sk, ci*sj*ck+si*sk;cj*sk, si*sj*sk+ci*ck, ci*sj*sk-si*ck;-sj, si*cj, ci*cj ];end
2. 姿态阵 -> 欧拉角:m2att
θ = arcsin ( C 32 ) { γ = − atan 2 ( C 31 , C 33 ) ψ = − atan 2 ( C 12 , C 22 ) ∣ C 32 ∣ ⩽ 0.999999 { γ = atan 2 ( C 13 , C 11 ) ∣ C 32 ∣ > 0.999.999 ψ = 0 \begin{array}{l}\theta=\arcsin \left(C_{32}\right) \\ \left\{\begin{array}{l}\gamma=-\operatorname{atan} 2\left(C_{31}, C_{33}\right) \\ \psi=-\operatorname{atan} 2\left(C_{12}, C_{22}\right)\end{array}\left|C_{32}\right| \leqslant 0.999999\right. \\ \left\{\begin{array}{ll}\gamma=\operatorname{atan} 2\left(C_{13}, C_{11}\right) & \left|C_{32}\right|>0.999 .999 \\ \psi=0\end{array}\right. \\\end{array} θ=arcsin(C32){γ=−atan2(C31,C33)ψ=−atan2(C12,C22)∣C32∣⩽0.999999{γ=atan2(C13,C11)ψ=0∣C32∣>0.999.999
function [att, attr] = m2att(Cnb)
% Convert direction cosine matrix(DCM) to Euler attitude angles.
% 姿态阵 -> 欧拉角
% Prototype: [att, attr] = m2att(Cnb)
% Input: Cnb - DCM from navigation-frame(n) to body-frame(b)
% Outputs: att - att=[pitch; roll; yaw] in radians, in yaw->pitch->rollatt = [ asin(Cnb(3,2));atan2(-Cnb(3,1),Cnb(3,3)); atan2(-Cnb(1,2),Cnb(2,2)) ];if nargout==2 % dual Euler anglesattr = [ atan2(Cnb(3,2),Cnb(3,3)); asin(-Cnb(3,1)); atan2(Cnb(2,1),Cnb(1,1)) ];end
3. 四元数 -> 姿态阵:q2mat
C b n = [ q 0 2 + q 1 2 − q 2 2 − q 3 2 2 ( q 1 q 2 − q 0 q 3 ) 2 ( q 1 q 3 + q 0 q 2 ) 2 ( q 1 q 2 + q 0 q 3 ) q 0 2 − q 1 2 + q 2 2 − q 3 2 2 ( q 2 q 3 − q 0 q 1 ) 2 ( q 1 q 3 − q 0 q 2 ) 2 ( q 2 q 3 + q 0 q 1 ) q 0 2 − q 1 2 − q 2 2 + q 3 2 ] \boldsymbol{C}_{b}^{n}=\left[\begin{array}{ccc}q_{0}^{2}+q_{1}^{2}-q_{2}^{2}-q_{3}^{2} & 2\left(q_{1} q_{2}-q_{0} q_{3}\right) & 2\left(q_{1} q_{3}+q_{0} q_{2}\right) \\ 2\left(q_{1} q_{2}+q_{0} q_{3}\right) & q_{0}^{2}-q_{1}^{2}+q_{2}^{2}-q_{3}^{2} & 2\left(q_{2} q_{3}-q_{0} q_{1}\right) \\ 2\left(q_{1} q_{3}-q_{0} q_{2}\right) & 2\left(q_{2} q_{3}+q_{0} q_{1}\right) & q_{0}^{2}-q_{1}^{2}-q_{2}^{2}+q_{3}^{2}\end{array}\right] Cbn= q02+q12−q22−q322(q1q2+q0q3)2(q1q3−q0q2)2(q1q2−q0q3)q02−q12+q22−q322(q2q3+q0q1)2(q1q3+q0q2)2(q2q3−q0q1)q02−q12−q22+q32
function Cnb = q2mat(qnb)
% Convert attitude quaternion to direction cosine matrix(DCM).
% 四元数 -> 姿态阵
% Prototype: Cnb = q2mat(qnb)
% Input: qnb - attitude quaternion
% Output: Cnb - DCM from body-frame to navigation-frameq11 = qnb(1)*qnb(1); q12 = qnb(1)*qnb(2); q13 = qnb(1)*qnb(3); q14 = qnb(1)*qnb(4); q22 = qnb(2)*qnb(2); q23 = qnb(2)*qnb(3); q24 = qnb(2)*qnb(4); q33 = qnb(3)*qnb(3); q34 = qnb(3)*qnb(4); q44 = qnb(4)*qnb(4);Cnb = [ q11+q22-q33-q44, 2*(q23-q14), 2*(q24+q13);2*(q23+q14), q11-q22+q33-q44, 2*(q34-q12);2*(q24-q13), 2*(q34+q12), q11-q22-q33+q44 ];
4. 姿态阵 -> 四元数:m2qua
q 0 2 + q 1 2 − q 2 2 − q 3 2 = C 11 q 0 2 − q 1 2 + q 2 2 − q 3 2 = C 22 q 0 2 − q 1 2 − q 2 2 + q 3 2 = C 33 q 0 2 + q 1 2 + q 2 2 + q 3 2 = 1 } ⇒ ∣ q 0 ∣ = 0.5 1 + C 11 + C 22 + C 33 ∣ q 1 ∣ = 0.5 1 + C 11 − C 22 − C 33 ∣ q 2 ∣ = 0.5 1 − C 11 + C 22 − C 33 ∣ q 3 ∣ = 0.5 1 − C 11 − C 22 + C 33 \left.\begin{array}{l}q_{0}^{2}+q_{1}^{2}-q_{2}^{2}-q_{3}^{2}=C_{11} \\ q_{0}^{2}-q_{1}^{2}+q_{2}^{2}-q_{3}^{2}=C_{22} \\ q_{0}^{2}-q_{1}^{2}-q_{2}^{2}+q_{3}^{2}=C_{33} \\ q_{0}^{2}+q_{1}^{2}+q_{2}^{2}+q_{3}^{2}=1\end{array}\right\} \Rightarrow \begin{array}{l}\left|q_{0}\right|=0.5 \sqrt{1+C_{11}+C_{22}+C_{33}} \\ \left|q_{1}\right|=0.5 \sqrt{1+C_{11}-C_{22}-C_{33}} \\ \left|q_{2}\right|=0.5 \sqrt{1-C_{11}+C_{22}-C_{33}} \\ \left|q_{3}\right|=0.5 \sqrt{1-C_{11}-C_{22}+C_{33}}\end{array} q02+q12−q22−q32=C11q02−q12+q22−q32=C22q02−q12−q22+q32=C33q02+q12+q22+q32=1⎭ ⎬ ⎫⇒∣q0∣=0.51+C11+C22+C33∣q1∣=0.51+C11−C22−C33∣q2∣=0.51−C11+C22−C33∣q3∣=0.51−C11−C22+C33
2 ( q 1 q 2 − q 0 q 3 ) = C 12 2 ( q 1 q 2 + q 0 q 3 ) = C 21 2 ( q 1 q 3 + q 0 q 2 ) = C 13 2 ( q 1 q 3 − q 0 q 2 ) = C 31 2 ( q 2 q 3 − q 0 q 1 ) = C 23 2 ( q 2 q 3 + q 0 q 1 ) = C 32 } ⇒ 4 q 0 q 1 = C 32 − C 23 4 q 0 q 2 = C 13 − C 31 4 q 0 q 3 = C 21 − C 12 4 q 1 q 2 = C 12 + C 21 4 q 1 q 3 = C 13 + C 31 4 q 2 q 3 = C 23 + C 32 } \left.\left.\begin{array}{l}2\left(q_{1} q_{2}-q_{0} q_{3}\right)=C_{12} \\ 2\left(q_{1} q_{2}+q_{0} q_{3}\right)=C_{21} \\ 2\left(q_{1} q_{3}+q_{0} q_{2}\right)=C_{13} \\ 2\left(q_{1} q_{3}-q_{0} q_{2}\right)=C_{31} \\ 2\left(q_{2} q_{3}-q_{0} q_{1}\right)=C_{23} \\ 2\left(q_{2} q_{3}+q_{0} q_{1}\right)=C_{32}\end{array}\right\} \Rightarrow \begin{array}{l}4 q_{0} q_{1}=C_{32}-C_{23} \\ 4 q_{0} q_{2}=C_{13}-C_{31} \\ 4 q_{0} q_{3}=C_{21}-C_{12} \\ 4 q_{1} q_{2}=C_{12}+C_{21} \\ 4 q_{1} q_{3}=C_{13}+C_{31} \\ 4 q_{2} q_{3}=C_{23}+C_{32}\end{array}\right\} 2(q1q2−q0q3)=C122(q1q2+q0q3)=C212(q1q3+q0q2)=C132(q1q3−q0q2)=C312(q2q3−q0q1)=C232(q2q3+q0q1)=C32⎭ ⎬ ⎫⇒4q0q1=C32−C234q0q2=C13−C314q0q3=C21−C124q1q2=C12+C214q1q3=C13+C314q2q3=C23+C32⎭ ⎬ ⎫
若仅根据式一,将难以确定四元数各元素的正负符号。如果已知四元数的某一个元素, 则根据式二可求解其他元素, 但须避免该已知元素为 0 。由四元数归一化条件 q 0 2 + q 1 2 q_{0}^{2}+q_{1}^{2} q02+q12 + q 2 2 + q 3 2 = 1 +q_{2}^{2}+q_{3}^{2}=1 +q22+q32=1 可知, 必然有 max ( q i 2 ) ⩾ 1 / 4 \max \left(q_{i}^{2}\right) \geqslant 1 / 4 max(qi2)⩾1/4 成立, 也就是说,四个元素中必然存在某个 ∣ q i ∣ ⩾ \left|q_{i}\right| \geqslant ∣qi∣⩾ 1 / 2 1 / 2 1/2 。实际应用时,可先根据式 一计算获得某一个较大的元素 q i q_{i} qi (不妨取为正值),再根据 式 (B. 10)计算剩余的其他三个元素。
function qnb = m2qua(Cnb)
% Convert direction cosine matrix(DCM) to attitude quaternion.
%
% Prototype: qnb = m2qua(Cnb)
% Input: Cnb - DCM from body-frame to navigation-frame
% Output: qnb - attitude quaternionC11 = Cnb(1,1); C12 = Cnb(1,2); C13 = Cnb(1,3); C21 = Cnb(2,1); C22 = Cnb(2,2); C23 = Cnb(2,3); C31 = Cnb(3,1); C32 = Cnb(3,2); C33 = Cnb(3,3);
% q0t = 0.5*sqrt(1+C11+C22+C33);
% q1t = 0.5*sqrt(1+C11-C22-C33);
% q2t = 0.5*sqrt(1-C11+C22-C33);
% q3t = 0.5*sqrt(1-C11-C22+C33);if C11>=C22+C33q1 = 0.5*sqrt(1+C11-C22-C33); qq4 = 4*q1;q0 = (C32-C23)/qq4; q2 = (C12+C21)/qq4; q3 = (C13+C31)/qq4;elseif C22>=C11+C33q2 = 0.5*sqrt(1-C11+C22-C33); qq4 = 4*q2;q0 = (C13-C31)/qq4; q1 = (C12+C21)/qq4; q3 = (C23+C32)/qq4;elseif C33>=C11+C22q3 = 0.5*sqrt(1-C11-C22+C33); qq4 = 4*q3;q0 = (C21-C12)/qq4; q1 = (C13+C31)/qq4; q2 = (C23+C32)/qq4;elseq0 = 0.5*sqrt(1+C11+C22+C33); qq4 = 4*q0;q1 = (C32-C23)/qq4; q2 = (C13-C31)/qq4; q3 = (C21-C12)/qq4;endqnb = [q0; q1; q2; q3];
5. 欧拉角 -> 四元数:a2qua
惯导姿态更新算法中常用的是四元数,惯导的输出结果常表示为欧拉角,需要进行四元数和欧拉角的相互转换,根据单位四元数的几何意义得:
Q b n = Q ψ ∘ Q θ ∘ Q γ = ( c ψ / 2 + k s ψ / 2 ) ∘ ( c θ / 2 + i s θ / 2 ) ∘ ( c γ / 2 + j s γ / 2 ) = ( c ψ / 2 c θ / 2 + i c ψ / 2 s θ / 2 + k s ψ / 2 c θ / 2 + k ∘ i ψ / 2 s θ / 2 ) ∘ ( c γ / 2 + j s γ / 2 ) = ( c ψ / 2 c θ / 2 + i c ψ / 2 s θ / 2 + k s ψ / 2 c θ / 2 + j s ψ / 2 s θ / 2 ) ∘ ( c γ / 2 + j s γ / 2 ) = [ c ψ / 2 c θ / 2 c γ / 2 − s ψ / 2 s θ / 2 s γ / 2 c ψ / 2 s θ / 2 c γ / 2 − s ψ / 2 c θ / 2 s γ / 2 s ψ / 2 s θ / 2 c γ / 2 + c ψ / 2 c θ / 2 s γ / 2 s ψ / 2 c θ / 2 c γ / 2 + c ψ / 2 s θ / 2 s γ / 2 ] \begin{aligned} \boldsymbol{Q}_{b}^{n}= & \boldsymbol{Q}_{\psi}{ }{\circ} \boldsymbol{Q}_{\theta} \circ \boldsymbol{Q}_{\gamma}=\left(c_{\psi / 2}+\boldsymbol{k} s_{\psi / 2}\right) \circ\left(c_{\theta / 2}+\boldsymbol{i} s_{\theta / 2}\right) \circ\left(c_{\gamma / 2}+\boldsymbol{j} s_{\gamma / 2}\right)= \\ & \left(c_{\psi / 2} c_{\theta / 2}+\boldsymbol{i} c_{\psi / 2} s_{\theta / 2}+\boldsymbol{k} s_{\psi / 2} c_{\theta / 2}+\boldsymbol{k} \circ \boldsymbol{i}_{\psi / 2} s_{\theta / 2}\right) \circ\left(c_{\gamma / 2}+\boldsymbol{j} s_{\gamma / 2}\right)= \\ & \left(c_{\psi / 2} c_{\theta / 2}+\boldsymbol{i} c_{\psi / 2} s_{\theta / 2}+\boldsymbol{k} s_{\psi / 2} c_{\theta / 2}+\boldsymbol{j} s_{\psi / 2} s_{\theta / 2}\right) \circ\left(c_{\gamma / 2}+\boldsymbol{j} s_{\gamma / 2}\right)= \\ & {\left[\begin{array}{l}c_{\psi / 2} c_{\theta / 2} c_{\gamma / 2}-s_{\psi / 2} s_{\theta / 2} s_{\gamma / 2} \\ c_{\psi / 2} s_{\theta / 2} c_{\gamma / 2}-s_{\psi / 2} c_{\theta / 2} s_{\gamma / 2} \\ s_{\psi / 2} s_{\theta / 2} c_{\gamma / 2}+c_{\psi / 2} c_{\theta / 2} s_{\gamma / 2} \\ s_{\psi / 2} c_{\theta / 2} c_{\gamma / 2}+c_{\psi / 2} s_{\theta / 2} s_{\gamma / 2}\end{array}\right] }\end{aligned} Qbn=Qψ∘Qθ∘Qγ=(cψ/2+ksψ/2)∘(cθ/2+isθ/2)∘(cγ/2+jsγ/2)=(cψ/2cθ/2+icψ/2sθ/2+ksψ/2cθ/2+k∘iψ/2sθ/2)∘(cγ/2+jsγ/2)=(cψ/2cθ/2+icψ/2sθ/2+ksψ/2cθ/2+jsψ/2sθ/2)∘(cγ/2+jsγ/2)= cψ/2cθ/2cγ/2−sψ/2sθ/2sγ/2cψ/2sθ/2cγ/2−sψ/2cθ/2sγ/2sψ/2sθ/2cγ/2+cψ/2cθ/2sγ/2sψ/2cθ/2cγ/2+cψ/2sθ/2sγ/2
function qnb = a2qua(att)
% Convert Euler angles to attitude quaternion.
% 欧拉角 -> 四元数
% Prototype: qnb = a2qua(att)
% Input: att - att=[pitch; roll; yaw] in radians
% Output: qnb - attitude quaternionatt2 = att/2;s = sin(att2); c = cos(att2);sp = s(1); sr = s(2); sy = s(3); cp = c(1); cr = c(2); cy = c(3); qnb = [ cp*cr*cy - sp*sr*sy;sp*cr*cy - cp*sr*sy;cp*sr*cy + sp*cr*sy;cp*cr*sy + sp*sr*cy ];
6. 四元数 -> 欧拉角:q2att
由四元数直接求解欧拉角并不容易,可以通过姿态阵作为中间过渡量。
θ = arcsin ( 2 ( q 2 q 3 + q 0 q 1 ) ) { γ = − atan 2 ( 2 ( q 1 q 3 − q 0 q 2 ) , q 0 2 − q 1 2 − q 2 2 + q 3 2 ) ψ = − atan 2 ( 2 ( q 1 q 2 − q 0 q 3 ) , q 0 2 − q 1 2 + q 2 2 − q 3 2 ) ∣ 2 ( q 2 q 3 + q 0 q 1 ) ∣ ⩽ 0.999999 } { γ = atan 2 ( 2 ( q 1 q 3 + q 0 q 2 ) , q 0 2 + q 1 2 − q 2 2 − q 3 2 ) ∣ 2 ( q 2 q 3 + q 0 q 1 ) ∣ > 0.999999 ψ = 0 \begin{array}{l}\theta=\arcsin \left(2\left(q_{2} q_{3}+q_{0} q_{1}\right)\right) \\ \left\{\begin{array}{ll}\gamma=-\operatorname{atan} 2\left(2\left(q_{1} q_{3}-q_{0} q_{2}\right), q_{0}^{2}-q_{1}^{2}-q_{2}^{2}+q_{3}^{2}\right) \\ \psi=-\operatorname{atan} 2\left(2\left(q_{1} q_{2}-q_{0} q_{3}\right), q_{0}^{2}-q_{1}^{2}+q_{2}^{2}-q_{3}^{2}\right) & \left|2\left(q_{2} q_{3}+q_{0} q_{1}\right)\right| \leqslant 0.999999\end{array}\right\} \\ \left\{\begin{array}{ll}\gamma=\operatorname{atan} 2\left(2\left(q_{1} q_{3}+q_{0} q_{2}\right), q_{0}^{2}+q_{1}^{2}-q_{2}^{2}-q_{3}^{2}\right) & \left|2\left(q_{2} q_{3}+q_{0} q_{1}\right)\right|>0.999999 \\ \psi=0\end{array}\right.\end{array} θ=arcsin(2(q2q3+q0q1)){γ=−atan2(2(q1q3−q0q2),q02−q12−q22+q32)ψ=−atan2(2(q1q2−q0q3),q02−q12+q22−q32)∣2(q2q3+q0q1)∣⩽0.999999}{γ=atan2(2(q1q3+q0q2),q02+q12−q22−q32)ψ=0∣2(q2q3+q0q1)∣>0.999999
function att = q2att(qnb)
% Convert attitude quaternion to Euler attitude angles.
% 四元数 -> 欧拉角
% Prototype: att = q2att(qnb)
% Input: qnb - attitude quaternion
% Output: att - Euler angles att=[pitch; roll; yaw] in radiansq11 = qnb(1)*qnb(1); q12 = qnb(1)*qnb(2); q13 = qnb(1)*qnb(3); q14 = qnb(1)*qnb(4); q22 = qnb(2)*qnb(2); q23 = qnb(2)*qnb(3); q24 = qnb(2)*qnb(4); q33 = qnb(3)*qnb(3); q34 = qnb(3)*qnb(4); q44 = qnb(4)*qnb(4);C12=2*(q23-q14);C22=q11-q22+q33-q44;C31=2*(q24-q13); C32=2*(q34+q12); C33=q11-q22-q33+q44;att = [ asin(C32); atan2(-C31,C33); atan2(-C12,C22) ];
7. 四元数 -> 等效旋转矢量:q2rv
function rv = q2rv(q)
% Convert transformation quaternion to rotation vector.
% 四元数 -> 等效旋转矢量
% Prototype: rv = q2rv(q)
% Input: q - transformation quaternion
% Output: rv - corresponding rotation vector, such thatif(q(1)<0)q = -q;endn2 = acos(q(1));if n2>1e-40k = 2*n2/sin(n2);elsek = 2;endrv = k*q(2:4); % q = [ cos(|rv|/2); sin(|rv|/2)/|rv|*rv ];
8. 等效旋转矢量 -> 四元数:rv2q
首先,将四元数转化为标量非负的四元数;其次,根据公式 Q = q 0 + q v = cos ϕ 2 + u sin ϕ 2 = Q=q_{0}+\boldsymbol{q}_{v}=\cos \frac{\phi}{2}+\boldsymbol{u} \sin \frac{\phi}{2}= Q=q0+qv=cos2ϕ+usin2ϕ= cos ϕ 2 + ϕ 2 ⋅ sin ( ϕ / 2 ) ϕ / 2 \cos \frac{\phi}{2}+\frac{\phi}{2} \cdot \frac{\sin (\phi / 2)}{\phi / 2} cos2ϕ+2ϕ⋅ϕ/2sin(ϕ/2), 先由四元数的标量关系 q 0 = cos ϕ 2 q_{0}=\cos \frac{\phi}{2} q0=cos2ϕ 求旋转矢量模值的一半 ϕ 2 = \frac{\phi}{2}= 2ϕ= arccos ( q 0 ) \arccos \left(q_{0}\right) arccos(q0), 再由矢量关系 q v = ϕ 2 ⋅ sin ( ϕ / 2 ) ϕ / 2 \boldsymbol{q}_{v}=\frac{\boldsymbol{\phi}}{2} \cdot \frac{\sin (\phi / 2)}{\phi / 2} qv=2ϕ⋅ϕ/2sin(ϕ/2) 求等效旋转矢量 ϕ = 2 ( ϕ / 2 ) sin ( ϕ / 2 ) q v \boldsymbol{\phi}=2 \frac{(\phi / 2)}{\sin (\phi / 2)} \boldsymbol{q}_{v} ϕ=2sin(ϕ/2)(ϕ/2)qv 。
Q = q 0 + q v = cos ϕ 2 + u sin ϕ 2 Q=q_{0}+\boldsymbol{q}_{v}=\cos \frac{\phi}{2}+\boldsymbol{u} \sin \frac{\phi}{2} Q=q0+qv=cos2ϕ+usin2ϕ
function q = rv2q(rv)
% Convert rotation vector to transformation quaternion.
%
% Prototype: q = rv2q(rv)
% Input: rv - rotation vector
% Output: q - corresponding transformation quaternion, such that
% q = [ cos(|rv|/2); sin(|rv|/2)/|rv|*rv ]q = zeros(4,1);n2 = rv(1)*rv(1) + rv(2)*rv(2) + rv(3)*rv(3);if n2<1.0e-8 % cos(n/2)=1-n2/8+n4/384; sin(n/2)/n=1/2-n2/48+n4/3840q(1) = 1-n2*(1/8-n2/384); s = 1/2-n2*(1/48-n2/3840);elsen = sqrt(n2); n_2 = n/2;q(1) = cos(n_2); s = sin(n_2)/n;endq(2) = s*rv(1); q(3) = s*rv(2); q(4) = s*rv(3);
9. 姿态阵 -> 等效旋转矢量:m2rv
function rv = m2rv(m)
% Convert transformation matrix to rotation vector.
%
% Prototype: rv = m2rv(m)
% Input: m - transformation matrix
% Output: rv - corresponding rotation vector, such thatrv = [m(3,2)-m(2,3); m(1,3)-m(3,1); m(2,1)-m(1,2)]; % 11/10/2022phi = acos((m(1,1)+m(2,2)+m(3,3)-1)/2);if phi<1e-10, afa=1/2; else afa=phi/(2*sin(phi)); end
% afa = phi/sqrt(rv'*rv);rv = afa*rv;return;
% rv = iaskew(m-glv.I33); % coarse init is ok when rv is small, otherwise may fail
% rvx = askew(rv); % good! the following iteration due to thefor k=1:2 % accuracy deduce of sqrt(.) in function m2quaxx = rv(1)*rv(1); xy = rv(1)*rv(2); xz = rv(1)*rv(3);yy = rv(2)*rv(2); yz = rv(2)*rv(3); zz = rv(3)*rv(3);n2 = xx+yy+zz;
% n2 = rv'*rv; if n2>1.0e-40n = sqrt(n2);
% rvx = (m-eye(3)-(1-cos(n))/n2*rvx*rvx) * (n/sin(n));rvx = (m1-(1-cos(n))/n2*[-yy-zz,xy,xz; xy,-xx-zz,yz; xz,yz,-xx-yy]) * (n/sin(n));rv = [rvx(3,2); rvx(1,3); rvx(2,1)]; % rv = iaskew(rvx);elserv = zeros(3,1);break;endend
10. 等效旋转矢量 -> 姿态阵:rv2m
C b i = I + sin ϕ ϕ ( ϕ × ) + 1 − cos ϕ ϕ 2 ( ϕ × ) 2 \boldsymbol{C}_{b}^{i}=\boldsymbol{I}+\frac{\sin \phi}{\phi}(\boldsymbol{\phi} \times)+\frac{1-\cos \phi}{\phi^{2}}(\boldsymbol{\phi} \times)^{2} Cbi=I+ϕsinϕ(ϕ×)+ϕ21−cosϕ(ϕ×)2
function m = rv2m(rv)
% Convert rotation vector to transformation matrix.
% 等效旋转矢量 -> 姿态阵
% Prototype: m = rv2m(rv)
% Input: rv - rotation vector
% Output: m - corresponding DCM, such thatxx = rv(1)*rv(1); yy = rv(2)*rv(2); zz = rv(3)*rv(3);n2 = xx+yy+zz;if n2<1.e-8a = 1-n2*(1/6-n2/120); b = 0.5-n2*(1/24-n2/720); % a->1, b->0.5elsen = sqrt(n2);a = sin(n)/n; b = (1-cos(n))/n2;endarvx = a*rv(1); arvy = a*rv(2); arvz = a*rv(3);bxx = b*xx; bxy = b*rv(1)*rv(2); bxz = b*rv(1)*rv(3);byy = b*yy; byz = b*rv(2)*rv(3); bzz = b*zz;m = zeros(3,3);% m = I + a*(rvx) + b*(rvx)^2;m(1)=1 -byy-bzz; m(4)= -arvz+bxy; m(7)= arvy+bxz;m(2)= arvz+bxy; m(5)=1 -bxx-bzz; m(8)= -arvx+byz;m(3)= -arvy+bxz; m(6)= arvx+byz; m(9)=1 -bxx-byy;
11. 反对称阵
askew:求三维向量的反对称阵
function m = askew(v)m = [ 0, -v(3), v(2); v(3), 0, -v(1); -v(2), v(1), 0 ];
(n))/n2;endarvx = a*rv(1); arvy = a*rv(2); arvz = a*rv(3);bxx = b*xx; bxy = b*rv(1)*rv(2); bxz = b*rv(1)*rv(3);byy = b*yy; byz = b*rv(2)*rv(3); bzz = b*zz;m = zeros(3,3);% m = I + a*(rvx) + b*(rvx)^2;m(1)=1 -byy-bzz; m(4)= -arvz+bxy; m(7)= arvy+bxz;m(2)= arvz+bxy; m(5)=1 -bxx-bzz; m(8)= -arvx+byz;m(3)= -arvy+bxz; m(6)= arvx+byz; m(9)=1 -bxx-byy;
11. 反对称阵
askew:求三维向量的反对称阵
function m = askew(v)m = [ 0, -v(3), v(2); v(3), 0, -v(1); -v(2), v(1), 0 ];