leetCode 198.打家劫舍动态规划

198. 打家劫舍 - 力扣（LeetCode）

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

示例 1：

输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。

示例 2：

输入：[2,7,9,3,1]
输出：12
解释：偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。偷窃到的最高金额 = 2 + 9 + 1 = 12 。

>>思路和分析

常见困惑(•_•)? ：当前的状态我是偷呢还是不偷呢？
破解困惑：当前房屋偷与不偷取决于前一个房屋和前两个房屋是否被偷了~
当前状态和前面状态具有一种依赖关系，可用动规的递推公式

>>动规五部曲

1.确定dp数组（dp table）以及下标的含义

dp[i] : 考虑下标i（包括 i）以内的房屋，最多可以偷窃的金额为 dp[i]

2.确定递推公式

决定 dp[i] 的因素就是第 i 个房间 偷或者不偷

① 考虑偷的情况

如果偷第 i 个房间，那么 dp[i] = dp[i - 2] + nums[i] ，即: 第 i - 1 个房一定是不考虑的，找出下标 i - 2（包括 i - 2）以内的房屋，最多可以偷窃的金额为 dp[i - 2] 加上第 i 个房间偷到的钱。

② 考虑不偷的情况

如果不偷第 i 个房间，那么dp[i] = dp[i - 1]，即考虑 i - 1房（注意这里是考虑，并不是一定要偷 i - 1 ）

dp[i] 取这两种情况的最大值，即 dp[i] = max(dp[i - 2] + nums[i],dp[i - 1]);

3.dp数组初始化

从递推公式 dp[i] = max(dp[i - 2] + nums[i],dp[i - 1]);可以看出，递推公式的基础就是dp[0] 和 dp[1]。

dp[0] = nums[0];
dp[1] = max(nums[0],nums[1]);

vector<int> dp(nums.size());
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);

4.确定遍历顺序

dp[i] 是根据 dp[i - 2] 和 dp[i - 1] 推导出来的，那么一定是从前到后遍历！！！

for (int i = 2; i < nums.size(); i++) {dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
}

5.举例推导 dp 数组

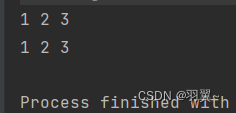
输入[2,7,9,3,1] 和 [2,7,9,6,1]

class Solution {
public:int rob(vector<int>& nums) {if (nums.size() == 0) return 0;if (nums.size() == 1) return nums[0];vector<int> dp(nums.size(),0);dp[0] = nums[0];dp[1] = max(nums[0],nums[1]);for(int i=2;i < nums.size();i++) {dp[i] = max(dp[i-1],dp[i-2] + nums[i]);}return dp[nums.size()-1];}
};// 时间复杂度: O(n)
// 空间复杂度: O(n)

时间复杂度: O(n)
空间复杂度: O(n)

>>参考和推荐文章、视频

代码随想录 (programmercarl.com)

动态规划，偷不偷这个房间呢？| LeetCode：198.打家劫舍_哔哩哔哩_bilibili

打家劫舍是DP解决的经典题目，这道题也是打家劫舍入门级题目，后面我们还会变种方式来打劫的。

来自代码随想录的课堂截图：