给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例 1：

输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：

输入：digits = ""
输出：[]

示例 3：

输入：digits = "2"
输出：["a","b","c"]

提示：

0 <= digits.length <= 4

digits[i] 是范围 ['2', '9'] 的一个数字。

---

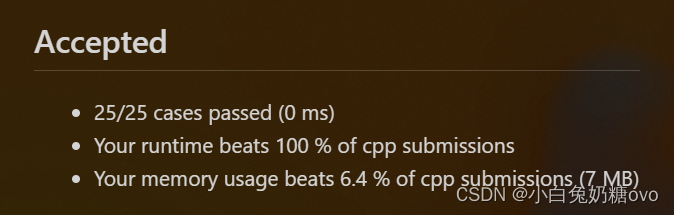
AC:

/** @lc app=leetcode.cn id=17 lang=cpp** [17] 电话号码的字母组合*/// @lc code=start
class Solution {
private:const string letterMap[10] = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz",};
public:string s;vector<string> result;void backtracking(const string& digits, int index) {if(digits.size() == index) {result.push_back(s);return ;}int digit = digits[index] - '0';string letter = letterMap[digit];for(int i = 0; i < letter.size(); i++){s.push_back(letter[i]);backtracking(digits, index + 1);s.pop_back();}}vector<string> letterCombinations(string digits) {s.clear();result.clear();if(digits.size() == 0)return result;backtracking(digits, 0);return result;}
};
// @lc code=end

The function uses a private member variable letterMap to map each digit to its corresponding set of letters. The letterMap is an array of strings, where each string represents the set of letters corresponding to a digit. For example, letterMap[2] is the string “abc”, which represents the letters ‘a’, ‘b’, and ‘c’ corresponding to the digit 2.

The function uses a recursive backtracking approach to generate all possible letter combinations. The backtracking function takes two arguments: the input string of digits and an index representing the current position in the input string. The function first checks if the current position is equal to the length of the input string. If so, it adds the current combination of letters to the result vector and returns.

If the current position is less than the length of the input string, the function retrieves the set of letters corresponding to the current digit using the letterMap array. It then iterates over each letter in the set and adds it to the current combination of letters. The function then recursively calls itself with the updated combination of letters and the next index. After the recursive call returns, the function removes the last letter from the combination of letters to backtrack and try the next letter in the set.

The letterCombinations function initializes the result vector and calls the backtracking function with the input string and an initial index of 0. If the input string is empty, the function returns an empty vector.

Overall, this implementation is a simple and efficient way to generate all possible letter combinations of a given string of digits using a backtracking algorithm. One possible way to improve the code would be to add error checking to ensure that the input string only contains digits. Additionally, the variable names could be more descriptive to make the code easier to read and understand.

---

How does the backtracking algorithm work in generating all possible letter combinations?

The backtracking algorithm used in this code works by recursively generating all possible letter combinations of a given string of digits. The algorithm uses a private member variable letterMap to map each digit to its corresponding set of letters.

The backtracking function takes two arguments: the input string of digits and an index representing the current position in the input string. The function first checks if the current position is equal to the length of the input string. If so, it adds the current combination of letters to the result vector and returns.

If the current position is less than the length of the input string, the function retrieves the set of letters corresponding to the current digit using the letterMap array. It then iterates over each letter in the set and adds it to the current combination of letters. The function then recursively calls itself with the updated combination of letters and the next index. After the recursive call returns, the function removes the last letter from the combination of letters to backtrack and try the next letter in the set.

The letterCombinations function initializes the result vector and calls the backtracking function with the input string and an initial index of 0 . If the input string is empty, the function returns an empty vector.

Overall, the backtracking algorithm works by generating all possible letter combinations of a given string of digits by recursively iterating over each digit and its corresponding set of letters. The algorithm uses a simple and efficient approach to generate all possible combinations of letters, and is a common technique used in many other combinatorial problems .