代谢组学是一门对某一生物或细胞所有低分子质量代谢产物(以相对分子质量<1000的有机和无机的代谢物为研究核心区)进行分析的新兴学科。因此从复杂的代谢组学数据中确定与所研究的现象有关的代谢物,筛选出候选生物标记物成为代谢物组学研究的热点和难点。
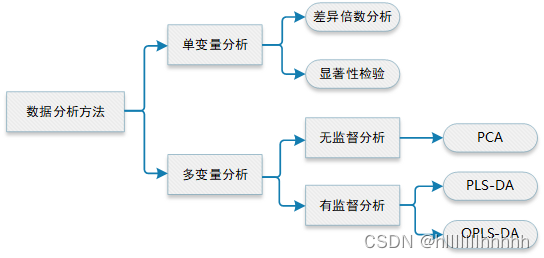
代谢组学分析数据用于统计分析时,数据集通常为一个N × K的矩阵(X矩阵),N表示N个样本数,每一行代表一个样品, K表示K个变量,每一列代表一个变量,在代谢组学中变量通常是指代谢物含量。最常用的分析方法如图1所示:
单变量分析方法
单变量分析方法仅分别分析单个变量,不考虑多个变量的相互作用与内在联系。具有简单性、易应用性和可解释性。但是无法基于整体数据对所测样品的优劣、差异进行综合评价和分析。
差异倍数分析
差异倍数变化大小(Fold Change,FC)表示实验组与对照组的含量比值,可以快速考察各个代谢物在不同组别之间的含量变化大小。
显著性检验
p值即概率,反映某一事件发生的可能性大小,用于区分该变量是否具有统计显著性,通常认为p<0.05具有统计显著性。常用的检验方法有t-test、方差分析(Analysis of Variance, ANOVA),但是由于代谢组学的变量较多,必要时需要进行多重假设检验,对p值进行校正,减少Ⅰ类错误,降低假阳性。
多变量分析
多变量分析分为无监督分析方法和有监督分析方法。在代谢组学分析中无监督学习有主成分分析(Principal Component Analysis,PCA),只需要数据集X,而有监督分析方法主要是偏最小二乘判别分析(Partial Least Squares Discrimination Analysis, PLS-DA)和正交偏最小二乘判别分析(Orthogonal Partial Least Squares Discrimination Analysis , OPLS-DA),这类方法在分析时除了需要数据集X,还需对样品进行指定并分组, 这样分组后模型将自动加上另外一个隐含的数据集Y,通常Y的赋值用-1/1或者0/1表示类别信息。
PCA
PCA是一种使用最广泛的数据降维算法,先找出数据X矩阵的方差最大方向作为PC1,在与PC1正交的平面中找出使得方差最大的作为PC2,依次类推。从而建立低维平面或空间 (通常2~5 维), 以此分析和概览整个数据集。PCA不是一种分类方法,但能提供对复杂数据集的直观解释,并从中揭示出数据集中观测数据的分组、趋势以及离群。对明显不同于大部分样品的离群样品,可加以甄别或剔除。如图2所示。另外,如果存在质控样品,PCA还可进行质控,如果质控样品很分散或具有一定的变化趋势,则说明检测质量存在一定的问题。
PLS-DA
PLS-DA在降维的同时结合了回归模型,并利用一定的判别阈值对回归结果进行判别分析。通过多元线性回归技术来找到数据集(X)和类别数据集(Y)之间的最大协方差的方向,建立两个独立数据集 (X−Y) 潜在关联分析方法, 即基于 X 变量数据信息, 建立Y 变量预测模型 (X→Y)。
这种模型计算的方法强行把各组分开, 有利于发现不同组间的异同点。对于组间差异不够明显的样品, 采用PCA 方法常常无法区分样品的组间差异, 这种情况下采用PLS-DA 模型可能更加有效。如图3所示。同时也能识别潜在的生物标记物,适用于两组或者两组以上分析,在需要同时观察多组别样品相似性和差异性时体现更大价值。但是如果主成分过多或分组过于复杂而出现过拟合现象 (over-fitting), 会造成模型失真, 在实际数据分析时应注意验证模型有效性和可靠性。
OPLS-DA
数据集X总会含有一些与研究无关的干扰信号,如人的生活方式,植物的生长环境或检测仪器的噪音干扰等。若能滤掉这些噪音会有助于发现最重要的变量,提高模型的有效性。
与PLS相比,OPLS根据数据集Y的差异将数据集X的差异分为两个部分,第一部分代表与Y相关的差异, 第二部分代表与Y不相关 (正交垂直)的差异,OPLS-DA可将这两部分差异进行区分,控制与Y正交或者无关的X的变化并加以滤除。通过这种方式,OPLS-DA可以更好地区分组间差异,提高模型的有效性和解析能力。如图4所示,OPLS-DA将组间差异主要集中在第一个预测主成分上,即X轴。OPLS-DA常用于对两组样品的代谢组学数据进行判别分析, 能清晰展现组间样品差别并能直接解释和识别潜在的生物标志物。