问题

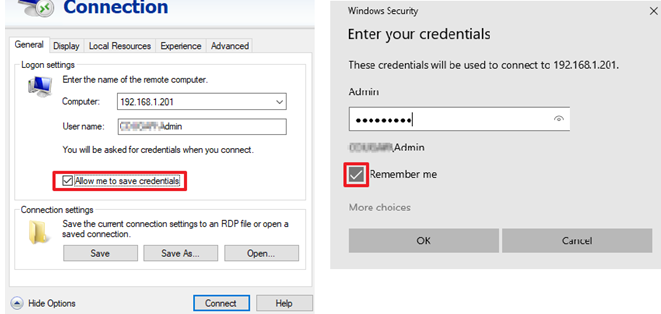
即使如下两项都打勾，其还是无法保存凭据，特别是连接Ubuntu (freerdp server)：

解决方法

网上多种复杂方法，不生效，其思路是修改后台配置，以使mstsc跟平常一样自动记住凭据。最后，如下的思路方法，最靠谱，即去Credential Manager中手动添加凭据。

1. 在控制面板中打开凭据管理器

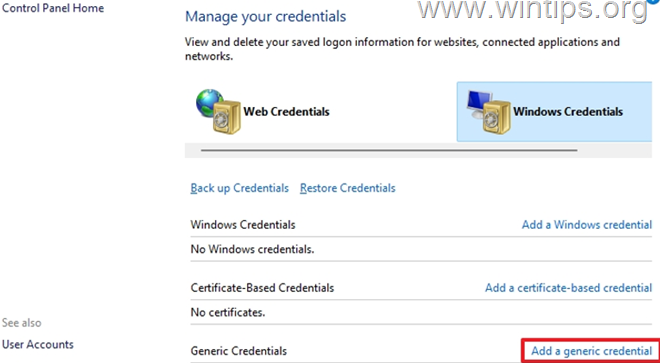
2. 选择添加通用凭证

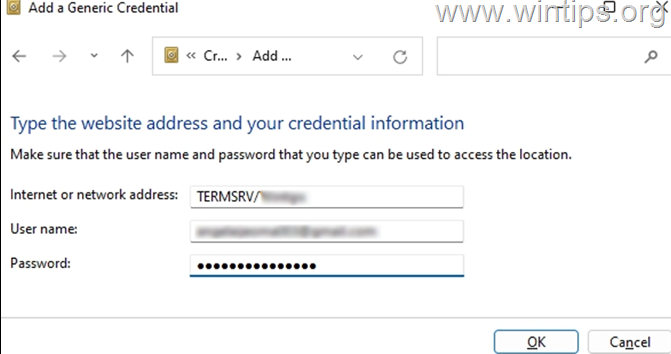
4. 在“因特网或网络地址”字段中，键入 TERMSRV/，然后输入远程计算机的名称或 IP 地址。然后键入 RDP 连接的用户名和密码，然后单击“确定”。
   *注意：互联网或网络地址必须以 TERMSRV/ 开头，后跟 PC 名称或 IP 地址。e…g “TERMSRV/10.199.212.49”。
   
5. 关闭凭据管理器并连接到 RDP。