长剖的本质是一种贪心。（启发式合并本质也是类似哈夫曼树的过程）

在此题中，首先肯定变直径，然后选端点为根。然后选叶子。而每个叶子为了不重复计算，可以只计算其长剖后所在链的贡献。（本题精髓，用长剖来贪心）

然后钦定某个点必选，就是一种反悔贪心。很显然的思路是删掉排名 $2\ast k-1$ 的叶子，但考虑：

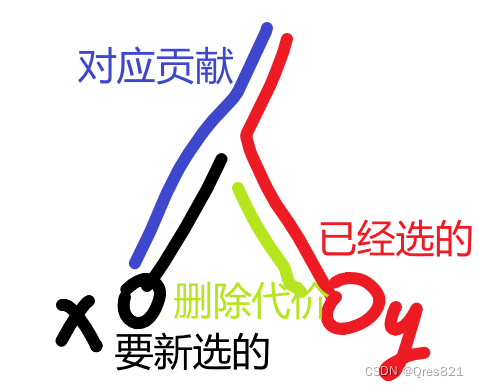
所以需要考虑离其最近被选的点

#include<bits/stdc++.h>
using namespace std;
//#define int long long
inline int read(){int x=0,f=1;char ch=getchar(); while(ch<'0'||
ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
//mt19937 rand(time(0));
//mt19937_64 rand(time(0));
//srand(time(0));
#define N 500010
//#define M
//#define mo
struct node { int x; long long y, z; };
int n, m, i, j, k, T, p1, p2, in[N];
int u, v, w, qe; 
vector<node>G[N]; struct Tree {int i, j, k, rt, mn[N]; long long h[N], mxh[N], mx[N], sum[N]; int son[N], dep[N], top[N]; int f[N][22], rk[N], dfn[N]; node w[N]; void dfs1(int x, int fa, int &p1) {//p1 p2if(h[x]>h[p1]) p1=x;  for(auto t : G[x]) {int y=t.y; long long z=t.z; if(y==fa) continue; h[y]=h[x]+z; dfs1(y, x, p1); }}void dfs2(int x, int fa) { //son[x] h[x] dep[x]dep[x]=dep[fa]+1; mx[x]=mxh[x]=h[x]; for(auto t : G[x]) {int y=t.y; long long z=t.z; if(y==fa) continue; h[y]=h[x]+z; 
//			printf("%lld(%lld) --%lld-> %lld(%lld)\n", x, h[x], z, y, h[y]); dfs2(y, x); mx[x]=max(mx[x], mx[y]); if(mxh[y]>mxh[son[x]]) son[x]=y; }if(son[x]) mxh[x]=mxh[son[x]]; }void dfs3(int x, int fa, int tp) {//top[x] w[x] 
//		printf("> %d\n", tp); top[x]=tp; f[x][0]=fa; if(in[x]==1 && fa) {w[x].y=h[x]-h[f[top[x]][0]]; w[x].x=x; }for(auto t : G[x]) {int y=t.y; 			if(y==fa) continue; if(y==son[x]) dfs3(y, x, tp); else dfs3(y, x, y); }}void init() {
//		for(i=1; i<=n; ++i) printf("%d ", top[i]); printf("\n"); 
//		for(i=1; i<=n; ++i) printf("%d ", h[i]); printf("\n"); sort(w+1, w+n+1, [] (node x, node y) { return x.y<y.y; }) ; reverse(w+1, w+n+1); for(i=1; i<=n; ++i) {
//			printf("%lld(%lld) ", w[i].y, w[i].x); if(w[i].x) sum[i]=w[i].y, rk[w[i].x]=i, dfn[i]=w[i].x; sum[i]+=sum[i-1]; }
//		printf("\n"); for(k=1; k<=19; ++k) for(i=1; i<=n; ++i) f[i][k]=f[f[i][k-1]][k-1]; }void dfs4(int x, int fa) {if(in[x]==1 && fa) mn[x]=rk[x]; else mn[x]=1e9; for(auto t : G[x]) {int y=t.y, z=t.z; if(y==fa) continue; dfs4(y, x); mn[x]=min(mn[x], mn[y]); //排名最小 }}int tiao(int x, int g) {for(k=19; k>=0; --k)if(mn[f[x][k]]>g) x=f[x][k]; return f[x][0]; }int lca(int x, int y) {if(x==y) return x; if(dep[x]<dep[y]) swap(x, y); for(int k=19; k>=0; --k)if(dep[f[x][k]]>=dep[y]) x=f[x][k]; if(x==y) return x; for(int k=19; k>=0; --k)if(f[x][k]!=f[y][k]) x=f[x][k], y=f[y][k]; return f[x][0]; }long long calc(int y, int oldy, int newx) {
//		printf("Lca(%d %d) : %d\n", oldy, newx, lca(oldy, newx)); 
//		return min(w[mn[y]].y, h[oldy]-h[lca(oldy, newx)]); return min(w[mn[y]].y, h[oldy]-h[y]); }long long que(int x, int k) {if(k==1) {
//			int y=dfn[mn[x]]; return h[y]; return mx[x]; }if(mn[x]<=2*k-1) {return sum[min(2*k-1, n)]; }int y=tiao(x, 2*k-1), newx, oldy; long long ans; newx=dfn[mn[x]]; oldy=dfn[mn[y]]; 
//		printf("%d | %d %d %d %d\n", y, newx, oldy, (h[newx]-h[y]), calc(y, oldy, newx)); ans=sum[2*k-1]-calc(y, oldy, newx)+(h[newx]-h[y]); ans=max(ans, sum[2*k-1]-w[2*k-1].y+(h[newx]-h[y])); return ans; }
}T1, T2;void print(long long x) {if(x) print(x/10), putchar(x%10+'0'); 
}signed main()
{
//	freopen("in.txt", "r", stdin);
//	freopen("out.txt", "w", stdout);freopen("bomb.in", "r", stdin);freopen("bomb.out", "w", stdout);
//	T=read();
//	while(T--) {
//
//	}n=read(); qe=read(); for(i=1; i<n; ++i) {u=read(); v=read(); w=read(); G[u].pb({u, v, w}); G[v].pb({v, u, w}); ++in[u]; ++in[v]; }T1.h[1]=0;  T1.dfs1(1, 0, p1); T1.h[p1]=0; T1.dfs1(p1, 0, p2);T1.rt=p1; T2.rt=p2; T1.h[p1]=0; T1.dfs2(p1, 0); T2.h[p2]=0; T2.dfs2(p2, 0); 
//	printf("%d %d\n", p1, p2); T1.dfs3(p1, 0, p1); T2.dfs3(p2, 0, p2); T1.init(); T2.init(); T1.dfs4(p1, 0); T2.dfs4(p2, 0); while(qe--) {u=read(); k=read(); print(max(T1.que(u, k), T2.que(u, k))); puts(""); }return 0;
}