文章目录
- 三种色面(黑白灰)
- 五种色调
这个可以参考素描对物体受光的理解:素描调子的基本规律与素描三大面五大调物体的明暗规律
三种色面(黑白灰)
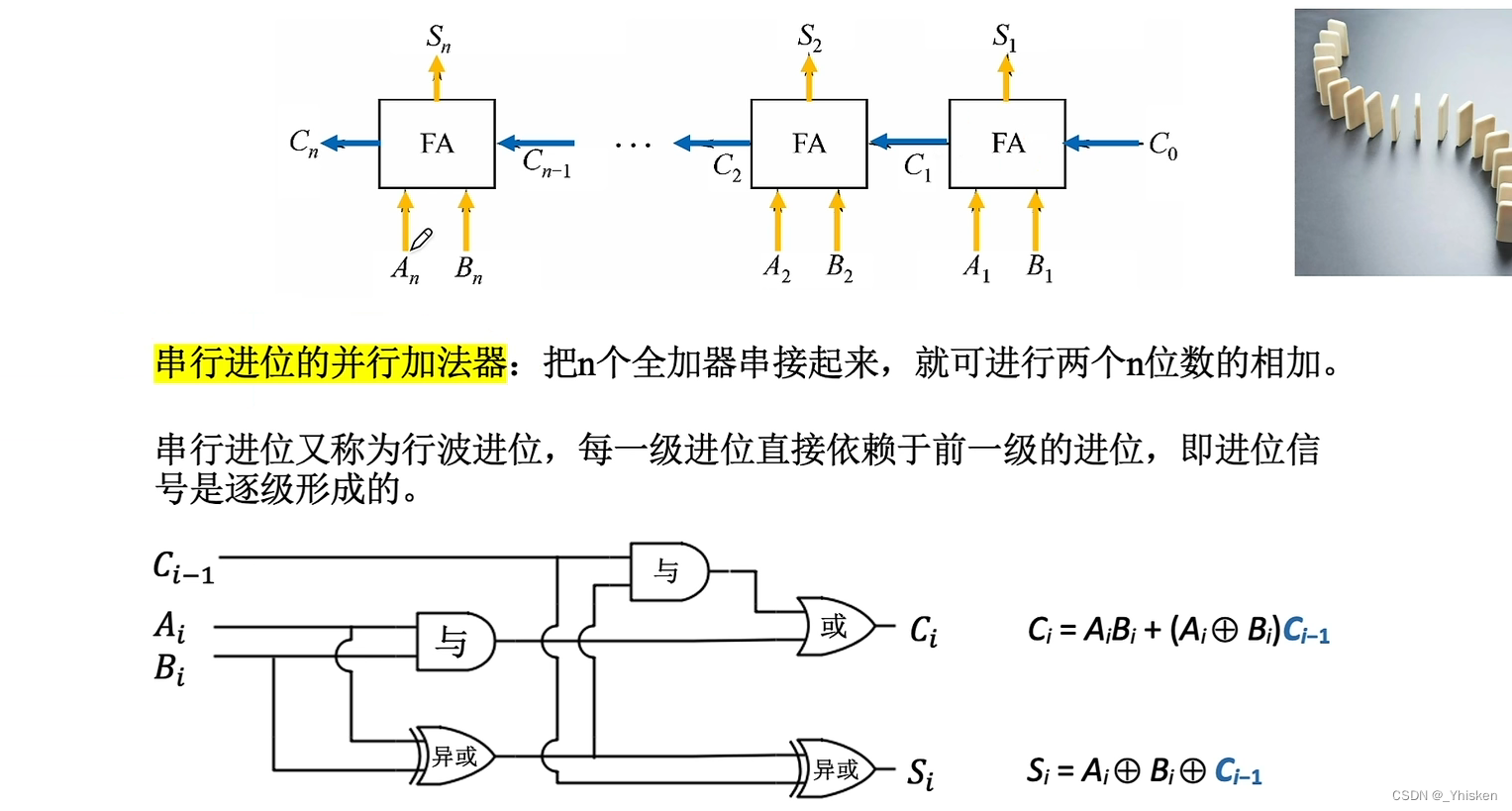
如下图所示,我们可以看到光源是从亮面所对应的方向射过来的,所以我们去分析图形的时候,首先要分析光从什么地方射过来?直接受光处则为亮面,侧面受光处为灰面也就是亮面跟暗面中间过渡的部分,光不能直接照射到的为暗面。

五种色调

1:受光面(亮面):是物体受光线90度直射的地方,这部分受光最大,调子淡,亮部的受光焦点叫“高光”,一般只有光滑的物体才能出现。
2:中间色(灰面):是物体受光侧射的部分,是明暗交界线的过渡地带,色阶接近,层次丰富。
3:明暗交界线:由于它受到环境光的影响,但又受不到主要光源的照射,因此对比强烈,给人的感觉调子最深!
4:反光部:暗部由于受周围物体的反射作用,会产生反光。反光作为暗部的一部分,一般要比亮部最深的中间颜色要深。
5:投影:就是物体本身影子的部分。它作为一个大的色块出现,也算五调子之一。投影的边沿近处清楚,渐远的模糊!







![[Python小项目] 从桌面壁纸到AI绘画](https://img-blog.csdnimg.cn/0bc7d48602ab4ac9b857e2f47aa5b50f.png)