文章目录
- 4.1 图式理论
- 4.2 马尔可夫链
- 4.3 进化算法的马尔可夫模型的符号
- 4.4 遗传算法的马尔可夫模型
- 4.4.1 选择
- 4.4.2 变异
- 4.4.3 交叉
- 4.5 遗传算法的动态系统模型
- 4.5.1 选择
- 4.5.2 变异
- 4.5.3 交叉
4.1 图式理论
- 图式是描述一组个体的位模式,其中用*来表示不在乎的位。
- 长度为l的图式总共有3^l种。
- 长度为l的位串属于2^l个图式。
- 在一个图式中有定义的位的个数称为此图式的阶,记为o。
- 在图式中从最左边的定义位到最右边定义位的位的个数称为定义长度.
- 属于某个图示的一个位串称为此图式的一个实例。
- 一般来说,一个图式含有的实例个数等于2^A,这里A是图式中星号的个数。
- 平均适应度:

- 第t+1代实例个数的期望等于适应度总和/平均适应度
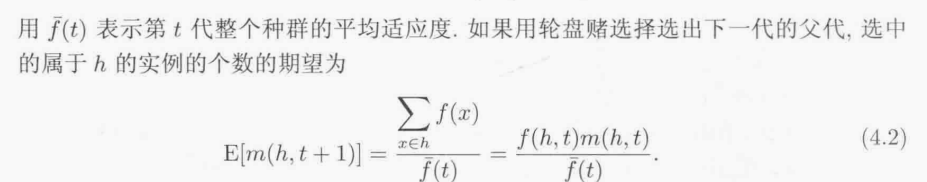
交叉破坏图式的概率: - 考虑图式h =1****.交叉不会破环这个图式.如果这个图式的一个实例与另一个位串交叉,至少会有一个子代仍是h的实例.
- 考虑图式h=11***.如果这个图式的一个实例与位串x交叉,交叉点可以有4个位置.如果交叉点在两个1位之间,图式可能会被破坏,它取决于x的值.如果交叉点在右边(另外三个可能的交叉点),图式就不会被破坏;至少有一个子代会是h的实例.由此可见,图式被破坏的概率小于或等于1/4,它取决于交叉发生的位置.
- 考虑图式h =1*1**.如果这个图式的一个实例与位串c交叉,则交叉点可以是4个位置中的其中一个.如果交叉点位于两个1位之间(有两个可能的交叉点),则图式可能被破坏,它取决于x的值.但是如果交叉点在最右边的1位的右边(另外两个可能的交叉点),则图式不会被破坏;至少有一个子代会是h的实例.由此可见,图式被破坏的概率小于或等于1/2,它取决于交叉发生的位置.
一般化:

变异概率:

泰勒展开:

类比:
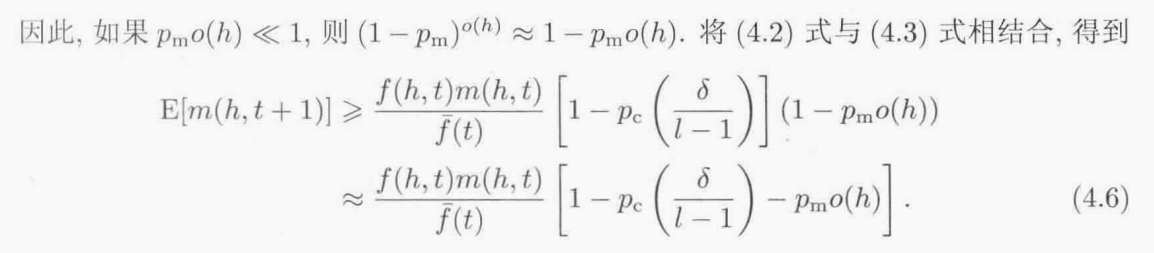
图式定理:


定理4.1 具有高于平均适应度值的短的低阶图式在遗传算法种群中的代表数会呈指数增长.
4.2 马尔可夫链
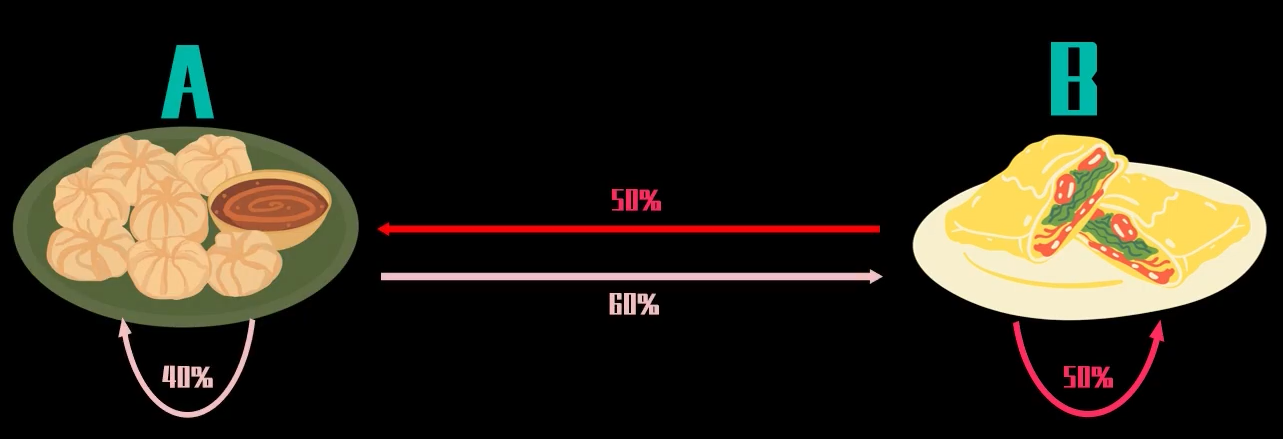
马尔可夫链的核心三要素:
- 状态空间
- 无记忆性
- 转移矩阵


假设在时刻1状态:
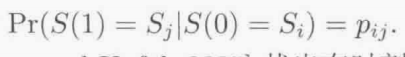
则在时刻2处于状态1的概率:
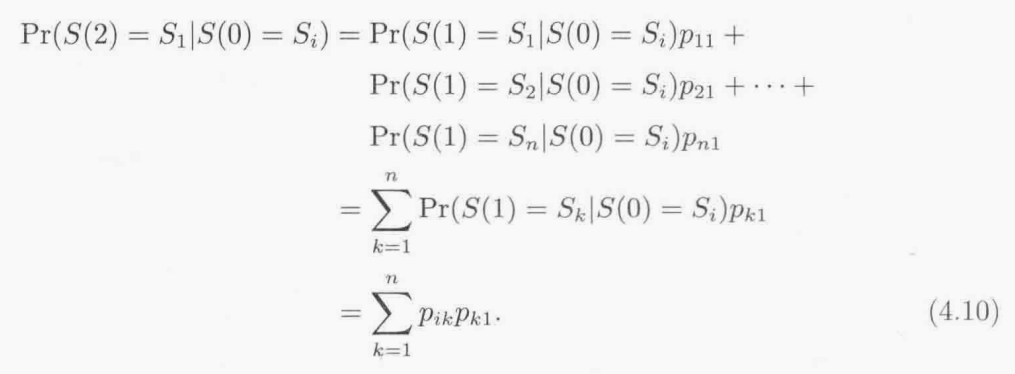
将上面的推导一般化,我们发现在时刻2过程处于状态j的概率为
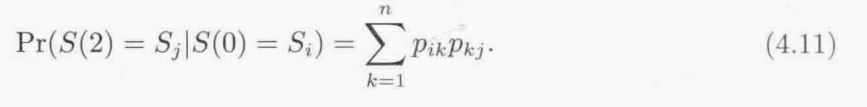
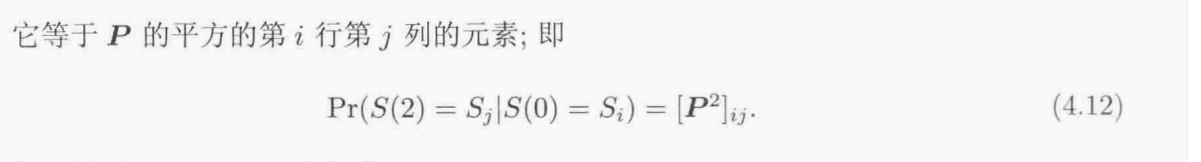
继续推理:




假设不知马尔可夫的初始状态,但是知道每个状态的概率,初始状态S(0)等于Sk的概率为pk(0),利用全概率定理得:
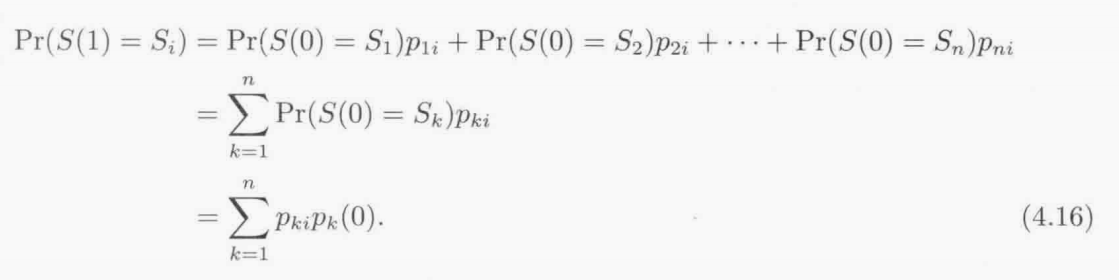
一般化:
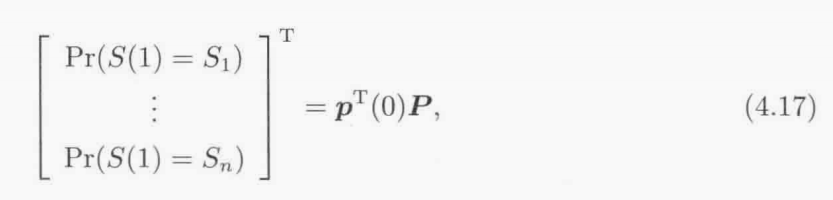




![Mybatis用Byte[]存图片,前端显示图片](https://img-blog.csdnimg.cn/edac2d8f303a4b9a955653e45c6b3684.png)