决策树是什么？决策树(decision tree)是一种基本的分类与回归方法。

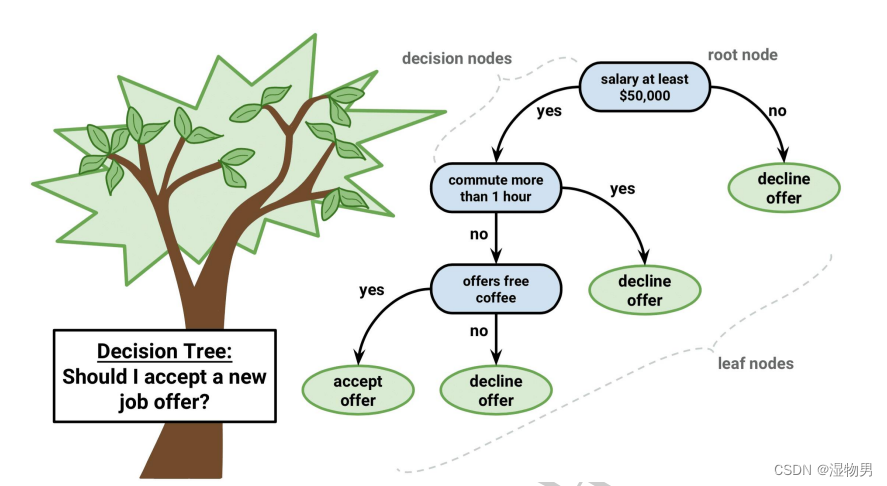
长方形代表判断模块 (decision block)，椭圆形成代表终止模块(terminating block)，表示已经得出结论，可以终止运行。从判断模块引出的左右箭头称作为分支(branch)，它可以达到另一个判断模块或者终止模块。我们还可以这样理解，分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点(node) 和有向边 (directed edge) 组成。结点有两种类型：内部结点 (internal node) 和叶结点(leaf node)。内部结点表示一个特征或属性，叶结点表示一个类。

决策树构建

特征选择在于选取对训练数据具有分类能力的特征。这样可以提高决策树学习的效率，如果利用一个特征进行分类的结果与随机分类的结果没有很大差别，则称这个特征是没有分类能力的。经验上扔掉这样的特征对决策树学习的精度影响不大。通常特征选择的标准是信息增益 (information gain) 或信息增益比，为了简单，本文使用信息增益作为选择特征的标准。那么，什么是信息增益？在讲解信息增益之前，让我们看一组实例，贷款申请样本数据表。

在划分数据集之后信息发生的变化称为信息增益，知道如何计算信息增益，我们就可以计算每个特征值划分数据集获得的信息增益，获得信息增益最高的特征就是最好的选择。

比较特征的信息增益，由于特征 A3(有自己的房子) 的信息增益值最大，所以选择 A3 作为最优特征。

它将训练集 D 划分为两个子集 D1(A3 取值为 “是”) 和 D2(A3 取值为 “否”)。由于 D1 只有同一类的样本点，所以它成为一个叶结点，结点的类标记为 “是”。对 D2 则需要从特征 A1(年龄)，A2(有工作) 和 A4(信贷情况) 中选择新的特征，计算各个特征的信息增益：

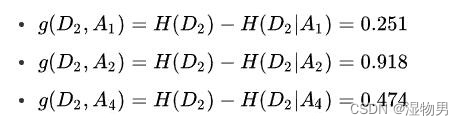
根据计算，选择信息增益最大的特征 A2(有工作) 作为结点的特征。由于 A2 有两个可能取值，从这一结点引出两个子结点：一个对应 “是”(有工作) 的子结点，包含 3 个样本，它们属于同一类，所以这是一个叶结点，类标记为 “是”；另一个是对应 “否”(无工作) 的子结点，包含 6 个样本，它们也属于同一类，所以这也是一个叶结点，类标记为 “否”。这样就生成了一个决策树，该决策树只用了两个特征 (有两个内部结点)，生成的决策树如下图所示。

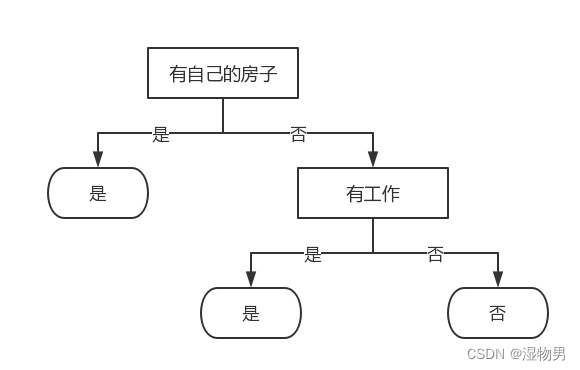
这种以信息增益为判断标准来构建决策树的方法为ID3

ID3在面对一个稀疏、有大量结点的特征时会出现问题

C4.5：使用信息增益率，解决ID3问题，考虑自身熵

CART：使用GINI系数来当做衡量标准

预剪枝方法

决策树过拟合风险很大，理论上可以完全分开数据，如果树足够庞大，每个叶子结点就是一个数据

• 预剪枝

限制深度，叶子结点个数，叶子结点样本数，信息增益量等

• 后剪枝

建立完决策树后进行剪枝操作

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

samples：当前结点所有样本数

value：不同类别样本的数量

通过一定的衡量标准，叶子结点越多，损失越大

$C_{\alpha }(T)=C(T)+\alpha \cdot \mid T_{leaf}\mid$