文章目录

Sigmoid函数是一种常用的数学函数,通常用于将实数映射到一个特定的区间。它的形状类似于"S"形状曲线,因此得名。Sigmoid函数在机器学习、神经网络和统计学中经常被使用,主要用于二元分类和处理概率值。
Sigmoid函数的一般形式如下:
[ \sigma(x) = \frac{1}{1 + e^{-x}} ]
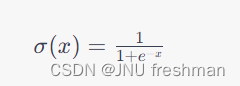
其中,(x) 是输入值,(\sigma(x)) 是对应的Sigmoid函数输出值,(e) 是自然对数的底数,也称为欧拉数,约等于2.71828。
以下是Sigmoid函数的一些关键特点和用途:
-
取值范围:Sigmoid函数的输出范围在0到1之间。这使得它特别适合用于表示概率值,因为它可以将任何实数映射到0和1之间。
-
平滑性:Sigmoid函数具有平滑的连续性质,这使得它在梯度下降等优化算法中非常有用。它的导数也容易计算,有助于反向传播算法在神经网络训练中的应用。
-
非线性特性:Sigmoid函数是一种非线性函数,这使得它能够处理非线性关系,因此在神经网络中作为激活函数广泛使用。在深度学习中,Sigmoid函数已经被一些更复杂的激活函数(如ReLU和Leaky ReLU)所取代,但它仍然有一些应用。
-
二元分类:Sigmoid函数常用于二元分类问题,其中它将模型的输出映射为一个表示概率的值。通常,当Sigmoid函数的输出大于0.5时,模型会预测为正类,否则为负类。
-
神经网络中的历史:在早期的神经网络中,Sigmoid函数是主要的激活函数之一。然而,由于一些问题(如梯度消失问题)和计算效率等原因,它后来被更复杂的激活函数所取代。
尽管Sigmoid函数在某些情况下被更现代的激活函数替代,但它仍然具有理论和历史意义,以及在某些应用中的实际价值。