Problem - F - Codeforces
题目大意:有一棵n个点的树,其中有k个标记点,令点i到所有标记点的最远距离为fi,问所有点中fi的最小值是多少
1<=k<=n<=2e5
思路:我们首先考虑取得最小值的点在哪,我们假设这棵树是一条链,链上有两个标记点,如下图
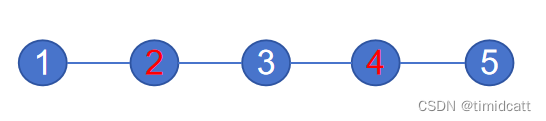
显然,在标记点2、4之间的点是才可能是取得最小值的点,因为如果在某一个点一段的话,这个最大值一定大于两个标记点之间的距离,而在中间的点一定都是小于这个距离的,那么在这两个点之间很显然最中间的点是取得最小值的点。
所以取最小值的点一定在两个标记点的正中间,同时这两个标记点要距离最远,答案距离就是这个距离除以2向上取整。
要找两个距离最远的标记点,我们从任意一点i出发bfs找到一个最远的标记点j,这时有两种情况,一种就是这i,j就是距离最远的两个点,另一种情况是i在j和距离j更远的点k之间,

如上图,从4出发找到最远的点2,但右边的5距离2更远,这时候因为2已经是最靠左的一个点了,所以只要再从2再跑一遍bfs,找到的最远的点和2一定是距离最远的两个点,类似于问以哪个标记点为根,能找到根到标记点的最远距离。
//#include<__msvc_all_public_headers.hpp>
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e5 + 5;
vector<pair<int,int>>fac;
int tot = 0;
int n;
int head[N];
struct Edge
{int v, next;
}e[N*2];
int mark[N];
void addedge(int u, int v)
{e[++tot].v = v;e[tot].next = head[u];head[u] = tot;
}
bool vis[N];
void init()
{for (int i = 1; i <= n; i++){vis[i] = 0;head[i] = -1;mark[i] = 0;}
}
void solve()
{int m;cin >> n;cin >> m;init();int it1 = -1;for (int i = 1; i <= m; i++){int x;cin >> x;mark[x] = 1;if (it1 == -1)it1 = x;//任意找一个标记点作为起始根}for (int i = 1; i <= n - 1; i++){int u, v;cin >> u >> v;addedge(u, v);addedge(v, u);}if (m == 1){//如果只有1个标记点,那取最小值的点点就是那个标记点cout << 0 << '\n';return;}queue<pair<int, int>>q;q.push({ it1,0 });int ma = 0, mai;vis[it1] = 1;while (!q.empty()){//bfs找到距离根最远的点int u = q.front().first, nd = q.front().second;q.pop();for (int i = head[u]; ~i; i = e[i].next){int v = e[i].v;if (vis[v])continue;vis[v] = 1;q.push({ v,nd + 1 });if (mark[v] && nd + 1 > ma){ma = nd + 1, mai = v;}}}q.push({ mai,0 });//以之前找到的最远标记点为新根vis[mai] = 1;ma = 0, mai = -1;for (int i = 1; i <= n; i++){vis[i] = 0;}while (!q.empty()){int u = q.front().first, nd = q.front().second;q.pop();for (int i = head[u]; ~i; i = e[i].next){int v = e[i].v;if (vis[v])continue;vis[v] = 1;q.push({ v,nd + 1 });if (mark[v] && nd + 1 > ma){ma = nd + 1, mai = v;}}}cout << (ma - 1) / 2 + 1;//答案就是最远距离/2cout << '\n';
}
int main()
{std::ios::sync_with_stdio(false);std::cin.tie(0);//FILE* stream1;//freopen_s(&stream1, "in.txt", "r", stdin);//freopen_s(&stream1, "out.txt", "w", stdout);int t;cin >> t;while (t--){solve();}return 0;
}