目录
一, 缓存
1, 什么是缓存
2, 什么是热点数据(热词)
3, 缓存更新策略
3.1 定期生成
3.2 实时生成
二, Redis缓存可能出现的问题
1, 缓存预热
1.1 什么是缓存预热
1.2 缓存预热的过程
2, 缓存穿透
2.1 什么是缓存穿透
2.2 缓存穿透产生的原因
2.3 缓存穿透的解决办法
3, 缓存雪崩
3.1 什么是缓存雪崩
3.2 缓存雪崩产生的原因
3.3 缓存雪崩的解决办法
4, 缓存击穿
4.1 什么是缓存击穿
4.2 缓存雪崩的解决办法
一, 缓存
1, 什么是缓存
Redis是一种内存数据库,最常用的场景就是作为缓存,加快用户查询的速度,核心思路就是把一些常用的数据(热点数据)放到触手可及(访问速度更快)的地方,方便随时读取.
1. 如何理解"触手可及"的地方?
硬件的访问速度,通常情况下:CPU寄存器 > 内存 > 硬盘 > 网络
硬盘相对于网络来说是"触手可及的",就可以使用硬盘作为网络的缓存(例如:浏览器的缓存,浏览器通过 http/https 从服务器上获取到如 html,css,js,图片,字体等进行展示,这些体积大又不会经常改变的数据就可以保存到浏览器本地硬盘,后续再打开这个页面的时候,就不必从网络上重新获取了)
2. 为什么说关系型数据库性能不⾼?
- 数据库把数据存储在硬盘上, 硬盘的 IO 速度并不快. 尤其是随机访问;
- 如果查询不能命中索引, 就需要进⾏表的遍历, 这就会⼤⼤增加硬盘 IO 次数;
- 关系型数据库对于 SQL 的执⾏会做⼀系列的解析, 校验, 优化⼯作;
- 如果是⼀些复杂查询, ⽐如联合查询, 需要进⾏笛卡尔积操作, 效率更是降低很多.
Redis作为缓存的图示:
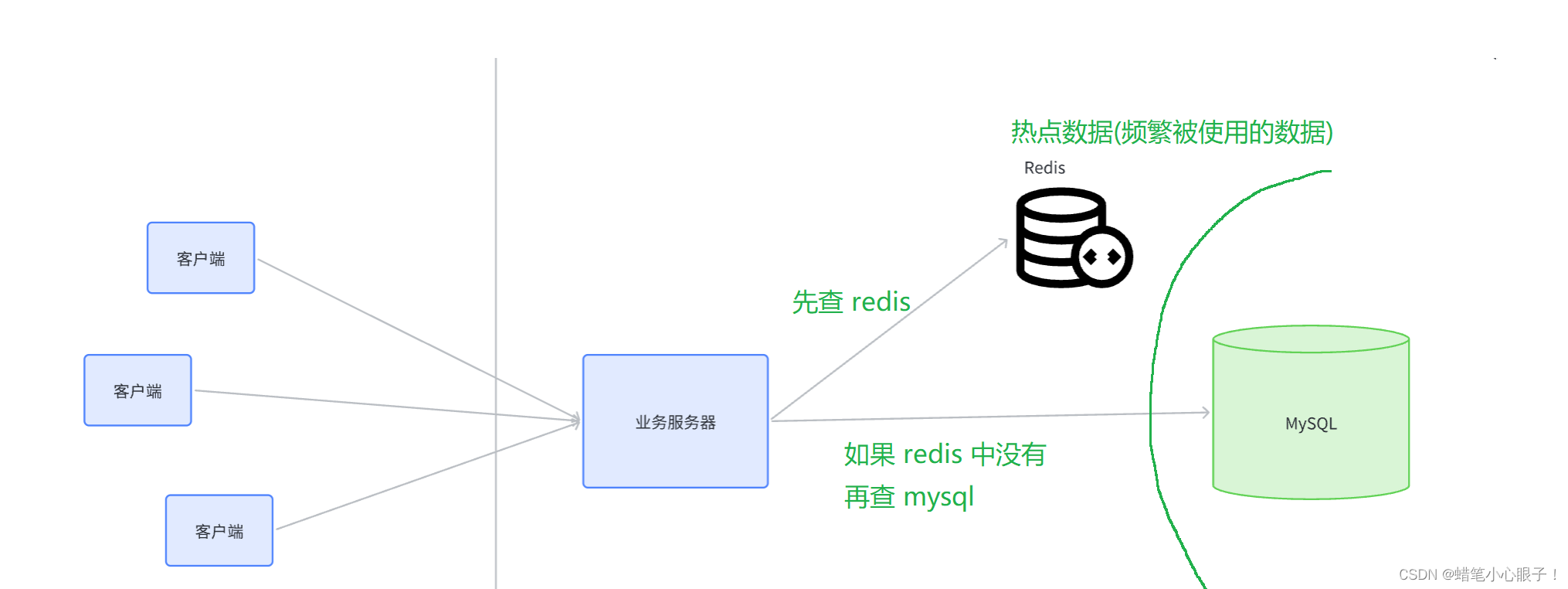
2, 什么是热点数据(热词)
注意:Redis作为缓存的时候访问速度相比mysql等关系型数据库更快,访问速度快代表着成本越高,所以相对而言Redis的存储空间更少,所以一般存储在Redis里面的数据都是一些经常被访问的数据,这部分数据就被称为热点数据.
Redis作为缓存的时候一般满足"二八原则",即20%的数据可以满足大部分的访问需求,因为一般用户进行访问的时候大部分访问的数据都是热点数据,这些数据已经存储在Redis中,所以访问速度很快,且很多访问都只会命中Redis,不会去数据库中查找,大大降低了访问数据库的并发量.
3, 缓存更新策略
3.1 定期生成
定期生成策略就是会把访问的数据以日志的形式记录下来,然后根据更新的频率(一天更新一次/一周更新一次等)进行统计,统计该频率内访问最多的前20%(根据实际场景决定)作为热点数据,将这些热点数据存储到Redis中,下次访问这些热点数据的时候就可以快速的从Redis中获取了.
优点:这种方式实现起来比较简单,过程更可控(缓存中有啥都是固定的),方便后期排查问题;
缺点:实时性不高,如果出现一些突发性问题,有一些本来不是热词的词突然变成热词,Redis中并没有,此时就会直接访问数据库,数据库会面临巨大的压力.
3.2 实时生成
实时生成策略就是如果查询的数据在Redis中有就直接访问,如果没有就会在数据库中查询,返回结果的同时也会将查询的结果写入Redis,这样Redis的数据也会随着查询数据库这个操作不断更新,经过一段时间的"动态平衡",Redis中的数据逐渐成为热点数据了.
问题:Redis的存储空间是有限的,随着不断的更新会逐渐达到Redis的内存上限(Redis的内存可通过配置文件中的maxmemory参数进行设定),如果此时达到内存上限了该怎么办?
答:达到内存上限需要对Redis内存中的数据进行淘汰,通用的淘汰策略有以下几种:
FIFO (First In First Out) 先进先出:把缓存中存在时间最久的(也就是最先来的数据)淘汰掉;
LRU (Least Recently Used) 淘汰最久未使⽤的:记录每个key最近访问时间,把最近访问时间最老的key淘汰掉;
LFU (Least Frequently Used) 淘汰访问次数最少的:记录每个key最近一段时间的访问次数,把访问次数最少得淘汰掉;
Random 随机淘汰:从所有key中抽取幸运儿被随机淘汰掉.
二, Redis缓存可能出现的问题
1, 缓存预热
1.1 什么是缓存预热
使⽤ Redis 作为 MySQL 的缓存的时候, 当 Redis 刚刚启动, 或者 Redis ⼤批 key 失效之后, 此时由于 Redis ⾃⾝相当于是空着的, 没啥缓存数据, 那么 MySQL 就可能直接被访问到, 从⽽造成较⼤的压⼒. 因此就需要提前把热点数据准备好, 直接写⼊到 Redis 中.,使 Redis 可以尽快为 MySQL 撑起保护伞.
1.2 缓存预热的过程
缓存预热结合了定期生成和实时生成两种策略,先通过离线的方式,通过一些统计途径,把一些热点数据找到一批,导入到Redis中,此时这部分热点数据就可以帮数据库承担很大的压力了,随着时间的推移,逐渐就使用新的热点数据淘汰掉旧的数据.
2, 缓存穿透
2.1 什么是缓存穿透
访问的key在Redis和数据库中都不存在,此时这样的key不会被放到缓存上,后续如果仍然再访问这个key的时候依然会访问到数据库,这样就会导致数据库承担的请求太多,压力很大,这种情况被称为缓存穿透.
2.2 缓存穿透产生的原因
- 业务设计的不合理,比如缺少必要的参数校验环节,导致非法的key也被查询了(这种情况最多);
- 开发/运维误操作,不小心把部分数据从数据库中删除了(少);
- 黑客恶意攻击(少).
2.3 缓存穿透的解决办法
- 针对要查询的参数进行严格的校验,比如要查询的key是用户的手机号,那么就需要校验当前key是否满足一个合法的手机号的格式;
- 针对数据库上不存在的key也需要在Redis中保存,该key所对应的value可以设置为空,避免后续频繁访问数据库;
- 使用布隆过滤器(本质上使用hash+bitmap的思想,能够用较少的空间判定某个元素是否存在)先判定key是否存在,再进行查询.
3, 缓存雪崩
3.1 什么是缓存雪崩
短时间内⼤量的 key 在缓存上失效, 导致数据库压⼒骤增, 甚⾄直接宕机
3.2 缓存雪崩产生的原因
大规模的key失效,可能性主要有两种:
- Redis挂了;
- Redis上的大量key同时失效(可能这些key设置了相同的过期时间).
3.3 缓存雪崩的解决办法
- 加强监控警报,加强Redis集群可用性的保证;
- 不给key设置过期时间或者不设置相同的过期时间(如添加随机因子从而避免同一时刻过期).
4, 缓存击穿
4.1 什么是缓存击穿
相当于缓存雪崩的特殊情况. 针对热点 key , 突然过期了, 导致⼤量的请求直接访问到数据库上, 甚⾄引起数据库宕机,缓存击穿区分于缓存雪崩的地方在于缓存击穿更加侧重于热点key.
4.2 缓存雪崩的解决办法
- 基于统计的方式发现热点key,并设置永不过期;
- 进行必要的服务降级,例如访问数据库的时候使用分布式锁,限制同时请求数据库的并发数.