传统的解决线性规划问题的方法是图形法、代数法求解，但是图形法解题有极大的局限性，因为一旦变量超过3个，基本上就无法通过图形解决，而代数法虽然可以解题，但对于复杂的问题可能效果较差甚至无法求解！
相比图形法和代数法，单纯形法解决线性规划问题具有以下优势：

1. 理论基础强：单纯形法是基于线性规划的基本理论，通过系统的迭代过程逐步逼近最优解。它是一种可行的、确定性的算法，能够找到问题的最优解或者确定问题是无界或无解的。
2. 高效性：在实践中，单纯形法通常能够在合理的时间内找到线性规划问题的最优解。尤其对于具有稀疏性质的问题，单纯形法的性能更为出色。此外，单纯形法的计算复杂度与问题规模的增长呈多项式关系。
3. 灵活性：单纯形法适用于各种类型的线性规划问题，包括有约束的和无约束的问题。它可以处理多目标函数、等式约束、不等式约束、非线性约束等多种情况。
4. 可以进行优化：单纯形法可以通过一些优化策略来提高算法的效率，例如早期停止条件、对偶单纯形法等。这些优化措施可以在实际应用中进一步加速算法的执行。
5. 可解释性强：单纯形法的迭代过程很容易理解和解释。每个迭代步骤都代表着一种改进，可以直观地解释为什么选择某个变量作为进基变量或出基变量，从而得到更优解。

尽管单纯形法具有以上优势，但对于大规模问题或非常稀疏的问题，单纯形法可能会遇到性能瓶颈。在这种情况下，可以考虑使用其他更高效的线性规划算法，例如内点法、启发式算法或者列生成法等。
具体使用单纯形法解题的步骤如下所示：

1. 化一般型为标准型，求初始基本可信解，建立初始单纯形表；
2. 求检验数并判断，若已得到最优解，结束计算；否则转入下一步；
3. 进行基变换，构建新的单纯形表进行迭代；
4. 重复步骤二、三，直到得出最优解、重复解或无最优解等。

1.化标准型

我们常见的线性规划模型的一般型为：
$$\begin{array}{rl}目标函数：& max(min)Z=\sum _{j=1}^n{c}_j{x}_j\\ 约束条件：& \{\begin{array}{c}{\sum }_{j=1}^n{a}_{ij}{x}_j\ge (⩽)b_i,i=1,2,\cdots ,m\\ \\ x_j\ge 0,j=1,2,\cdots ,n\end{array}\end{array}$$
单纯形法是一种求解线性规划问题的常用方法，其第一步是将线性规划问题转化为标准型，主要是为了方便后续的计算和迭代。
将线性规划问题转化为标准型的目的有以下几个方面：

1. 约束条件的统一表示：标准型可以将线性规划问题的约束条件统一表示为等式形式，即将不等式约束和非负约束都表示为等式约束。这样可以简化计算过程和算法的设计。
2. 约束条件的非负性：标准型要求所有变量的取值都非负，这样可以确保问题的可行解存在。通过引入松弛变量或人工变量，将不等式约束转化为等式约束，并引入非负约束，确保问题的可行性。
3. 目标函数的最大化或最小化：标准型要求将目标函数转化为最小化形式。对于最大化问题，可以通过将目标函数乘以-1来转化为最小化问题，并利用单纯形法求解。
   通过化为标准型，可以将线性规划问题转化为一个更加结构化和规范化的形式，方便应用单纯形法进行迭代计算。标准型的形式更加适合使用单纯形表格来表示和计算，使得单纯形法的步骤更加清晰和易于理解。
   需要注意的是，并非所有的线性规划问题都能够直接转化为标准型，有些问题需要经过一些额外的转化步骤才能达到标准型的形式。但是，一旦将问题转化为标准型，就可以直接应用单纯形法进行求解。
   具体线性规划模型的标准型为：
   $$\begin{array}{rl}目标函数：& maxZ=\sum _{j=1}^n{c}_j{x}_j\\ 约束条件：& \{\begin{array}{c}{\sum }_{j=1}^n{a}_{ij}{x}_j=b_i,i=1,2,\cdots ,m\\ \\ x_j\ge 0,j=1,2,\cdots ,n\end{array}\end{array}$$
   标准型的要求主要为：
   （1）目标函数为求最大值
   （2）约束条件均为等式方程
   （3）变量$x_j$为非负
   （4）常数$b_i$都大于等于零
   下面引入一个简单的例子并将其化为标准型：
   其线性规划问题的一般型为：
   $$\begin{array}{r}maxz=6x_1-2x_2+x_3\\ \{\begin{array}{c}2x_1-x_2+2x_3⩽2\\ x_1+4x_3⩽4\\ x_1,x_2,x_3⩾0\end{array}\end{array}$$
   将其转换为标准型为：
   $$\begin{array}{r}maxz=6x_1-2x_2+x_3+0x_4+0x_5\\ \{\begin{array}{c}2x_1-1x_2+2x_3+1x_4+0x_5=2\\ 1x_1+0x_2+4x_3+0x_4+1x_5=4\\ x_1,x_2,x_3,x_4,x_5\ge 0\end{array}\end{array}$$

2.求检验数并判断最优解

在单纯形法中，一旦将线性规划问题转化为标准型，可以通过以下步骤求解检验数，并判断是否达到最优解：

1. 制作初始单纯形表格：根据标准型的形式，构造初始单纯形表格，包括目标函数的系数、约束条件的系数矩阵、右侧常数项等。
2. 计算检验数：在初始单纯形表格中，计算每个变量的检验数。检验数表示在目标函数中增加或减少一个单位变量的值时，目标函数值的变化。检验数的计算公式为：检验数 = 目标函数系数 - 系数矩阵中对应列的系数与目标函数系数的乘积。
3. 判断是否达到最优解：若所有的检验数都为非负数，则当前解为最优解。因为如果存在负的检验数，将会导致目标函数值继续改善，因此需要进行下一步的迭代。
   具体初始单纯形表如下所示：
   
   注意，这里对参数进行解释：$c_k$表示各个变量的价值系数，这里可以从目标函数$maxz=6x_1-2x_2+x_3+0x_4+0x_5$可以看出各个变量（$x_1、x_2、x_3、x_4、x_5$）下面的数值，我们只需要看约束条件即可。
   $$\begin{array}{r}\{\begin{array}{c}2x_1-1x_2+2x_3+1x_4+0x_5=2\\ 1x_1+0x_2+4x_3+0x_4+1x_5=4\end{array}\end{array}$$
   $X_B$代表基变量，具体基变量的找法，我们只需要在系数矩阵中找到对应的单位矩阵，单位矩阵所对应的变量即为基变量，因此，从初始单纯形表可以看出，$x_4、x_5$即为基变量。
   $c_B$代表右侧基变量所对应的价值系数，初始单纯形表的基变量对应的价值系数分别是0、0
   $b$这一列称之为资源限量，填写的时候，只需要看系数矩阵中右侧的数字即可
   求基本可行解时，只需要设置全部非基变量为0，即令$x1、x2、x_3=0$,这样可以求出基变量$x_4=2,x_5=4$,所以基本可行解为$(0,0,0,2,4{)}^T$
   接下来，我们需要通过计算检验数来判断该解是否为最优解，即分别计算$(x_1、x_2、x_3、x_4、x_5)$所对应的检验数${\sigma }_j$,其计算方式为$c_j-c_B{x}_j$
   若当前计算的所有${\sigma }_j$都小于等于0，即表示当前基础可行解为最优解，否则还需要进行基变换来进一步求得最优解！

3.基变换

基变换的作用就会帮我们找到下一个可行解，简单来说就是用当前一个非基变量来替换基变量，也就是让非基变量入基，让基变量出基。
在确定哪个非基变量入基的时候，我们只需要看检验数，当前最大的检验数对应的变量，就是需要入基的非基变量，当前是$x_1$,它对应的检验数为6，是当前所有检验数的最大值。
接下来就需要确定出基变量，那么首先就需要计算$\theta$,其计算方法就是b这一列和确定入基$x_1$这一列相除得到，即为$(1,4{)}^T$,计算好$\theta$后，我们只需要找$\theta$值中的最小值，其最小值对应的变量$x_4$就是所对应的出基变量。
紧接着就需要把入基变量$x_1$和出基变量$x_4$中相交的数字经过行列运算变换为1，其对应的同列元素全部变换为0，计算完毕后就对应着下一个单纯形表。
具体下一个单纯形表如下所示：

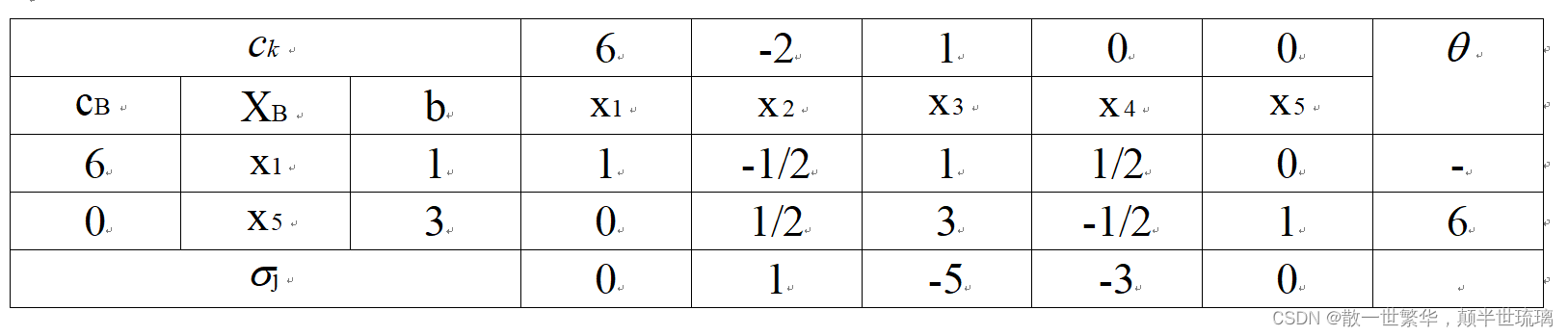
这里需要注意，你可能看到$\theta$对对应的第一个数填的是-,那是因为当前入基$x_2$对应的数字为负数，因此不需要计算。
由此可以看出，并不是所有的检验数都为小于等于零，因此，当前的基础可行解仍然不是最优解，所以还需要进一步进行基变换，下面就不对基变换的过程进行详解，仅仅展示最优求得最优解所对应的单纯形表。

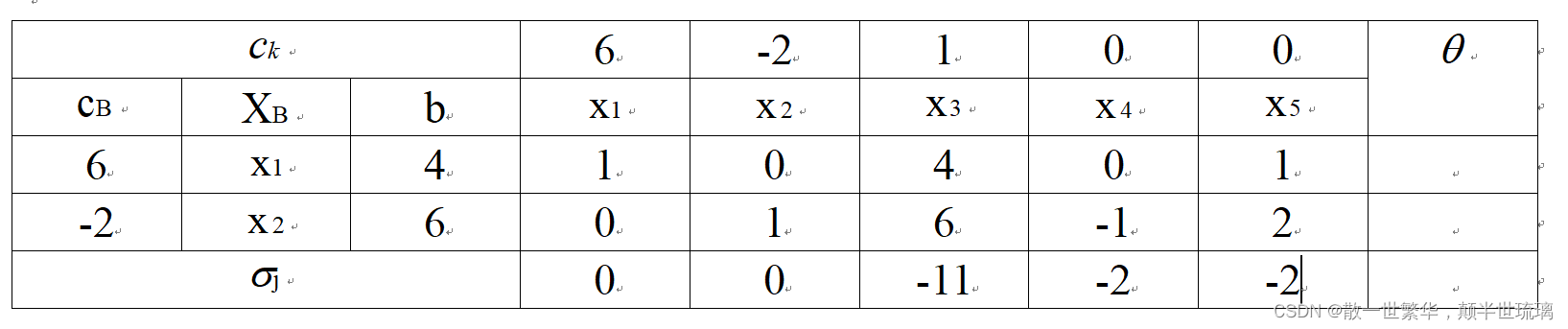
至此，从图表中可以看出，全部变量对应的检验数都小于等于0，因此，此时多对应的解为最优解，最优解为$(4,6,0,0,0{)}^T$

4.结果判定方法

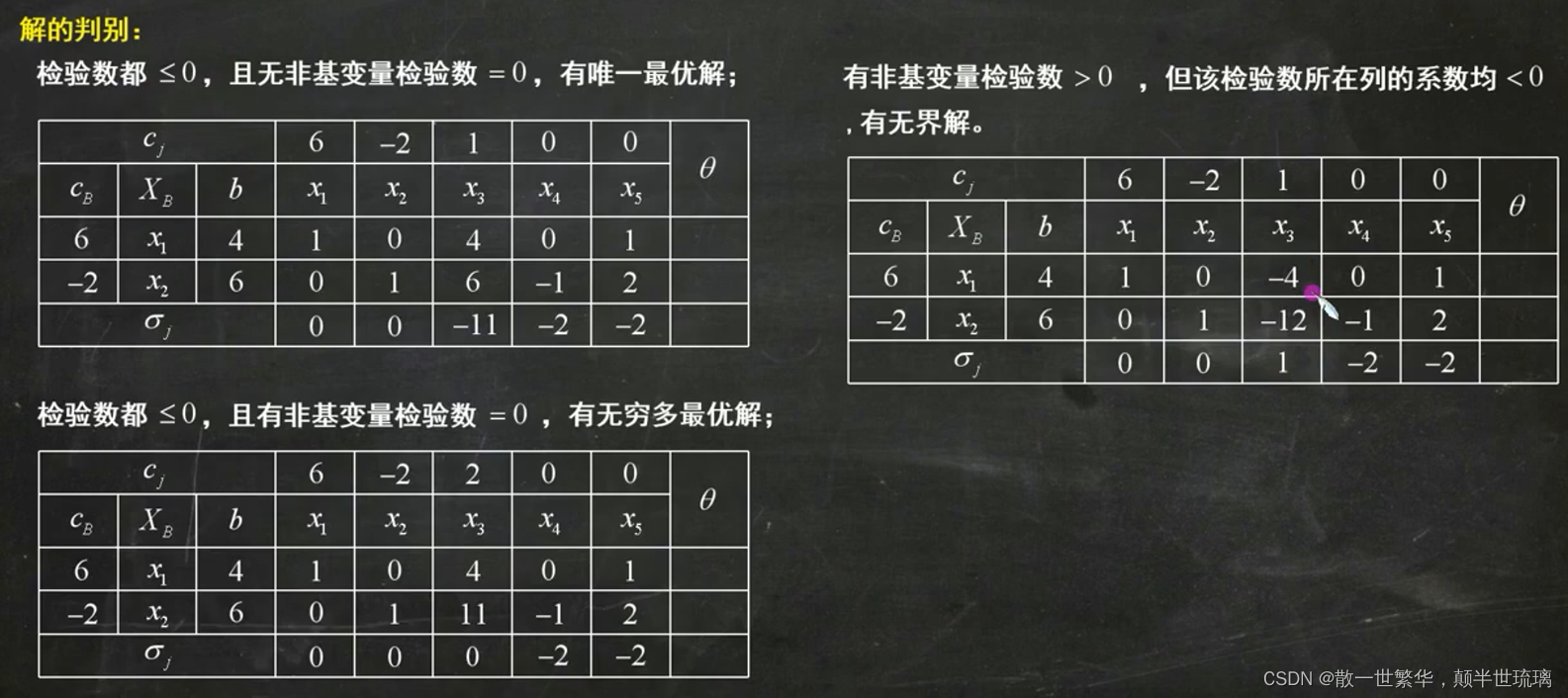
具体解的判定方法如下所示：