蚁群算法求包含34个国内城市的TSP，和最优解相差没那么大

文章目录

引言
蚁群觅食
算法原理
代码实现
- ACO求解TSP
- 整数规划求解TSP
相关阅读

引言

上一篇介绍的差分进化算法，很适合求解连续变量的优化问题；但针对组合优化问题，就不是很适用了。

至于哪一种智能优化算法更适合求解组合优化问题，我查阅了很多资料。不幸的是，虽然有很多公开测试数据集，但并没有令人信服的证据能表明某个智能优化算法是其中最好的。

即使如此，还是想找一个适合的智能优化算法来求解组合优化问题。一番权衡后，本文选择了蚁群算法，其中的原因包括以下两点：

蚁群算法的最初设计就是解决其中一大类组合优化问题，后续的应用几乎也都是组合优化问题，所以从天性上来说，两者是契合的；
蚁群算法最早是在1991年被提出的，而且持续有人在使用和研究，是一种经典的智能优化算法，所以具有学习的价值。

正文见下。

蚁群觅食

蚁群算法的设计借鉴了蚁群觅食的过程，因此为了能深刻地理解算法，有必要先了解清楚蚁群是如何觅食的。

研究发现，蚂蚁的食物搜索行为具有协作性。当蚂蚁在蚁穴和食物之间行走时，会释放一种被称为信息素的物质，这些物质形成一条指示轨迹。其他蚂蚁可以感知到环境中这种物质的存在和强度，在移动过程中，倾向于选择信息素强度高的轨迹。

以下图为例。 $t = 0$ 时刻，有20只蚂蚁位于A（蚁穴）处，要去往E（食物）处，另有20只蚂蚁位于E处，要返回A处。

$t = 1$ 时刻，20只蚂蚁从A到达B处的岔路口，因为此时没有信息素，所以10只蚂蚁走BCD路线，10只走BD路线，并分别在各自的路线上留下信息素；同理，从E出发的20只蚂蚁在D处也分成2个等数量的小组分别走DB和DCB路线，并留下信息素；另外，还有15只蚂蚁从A处开始出发。

到了 $t = 2$ 时，从E出发沿着DB路线的10只蚂蚁到达B处，而沿DCB行走的蚂蚁仅达到C处，因此此时BD路线上的信息素强度高于BCD路线；当另外15只从A出发的蚂蚁到达B处后，多数的蚂蚁（10只）会选择走BD路线，少量的蚂蚁（5只）选择走BCD路线。

这一正反馈机制会导致，BD路线上的信息素量相比BCD路线会越来越多，最终所有蚂蚁都找到BD这条最短路径。

算法原理

蚁群算法源于蚁群觅食，所以保留了一些类似的特征，比如个体间相互合作，通过信息素进行间接通信和正反馈机制等；但又高于蚁群觅食，主要体现在具有记忆能力，信息素的释放时机可以根据具体问题设定，允许局部优化、回退甚至预测能力等。

以下借助TSP问题（旅行商问题）实例，来详细描述蚁群算法的原理和和实现步骤。TSP问题指的是：旅行家要旅行n个城市，要求各个城市经历且仅经历一次，然后回到出发城市，并要求所走的路程最短。

（1）在蚁群算法的每一代循环中，每只蚂蚁都会独立地完成自己的TSP。蚂蚁完成TSP的过程中，不会选择已经访问过的城市，并且依赖状态转移概率选择下一个城市 $j$ 。状态转移概率的定义为：设第 $k$ 只蚂蚁当前所在的城市为 $i$ ，则从该城市移动到 $j$ 城市的状态转移概率为

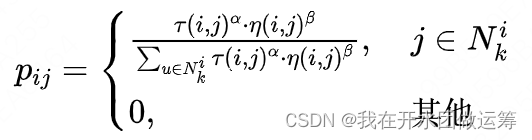
其中， $\tau (i,j)$ 是城市对 $(i, j)$ 上的信息素，下一段再细说； $\eta (i,j)$ 是城市对 $(i, j)$ 上的启发信息，在TSP问题中， $\eta (i,j)$ 一般选取为城市间距离的倒数。 $N_k^i$ 是所有未经过的城市组成的集合， $\alpha,\beta$ 分别表示信息素和启发信息相对权重参数，它们控制 $\tau (i,j)$ 和 $\eta (i,j)$ 在决策中所占的比重。显然，信息素越多，距离越短，被选择的概率就越大。

（2）初始的信息素设置成所有城市对均相同即可。当所有蚂蚁完成了自己的TSP后，会根据自己选择的路径和路径总长度留下不同强度的信息素 $\tau (i,j)$ 。用 $\Delta\tau_{i,j}^k$ 表示第 $k$ 只蚂蚁在城市对 $(i, j)$ 上释放的量。在Ant Cycle System中，其值为

其中，$Q$是常数，$L_k$表示第$k$只蚂蚁在本次循环中所走路径的长度。显然，解的质量越好，在所经过的路径上留下的信息素$\Delta\tau_{i,j}^k$就越大。

所以，针对城市对 $(i, j)$ 上，信息素的总改变量为
$\Delta\tau_{i,j}=\sum_{k=1}^m \Delta\tau_{i,j}^k$
其中， $m$ 为蚂蚁数。

此外，算法中还引入了信息素会发机制。设信息素的保持系数为 $\rho$ ，则在完成一次完整循环后，信息素的值变为
$\tau_{i,j} = \rho\tau_{i,j} + \Delta\tau_{i,j}$

（3）判断是否达到退出条件，如果满足，则退出，否则便进入下一代循环。

代码实现

ACO求解TSP

求解随机生成的TSP实例，感觉有些太普通。所以决定加点难度，试着沿国内34个主要城市跑一圈，并把优化后的最短TSP可视化出来。

以下是Python代码。感恩网上大量的开源代码，让我完成可以少花很多时间来完成这些代码，同时保证TSP可视化后的颜值。

import math
import timeimport numpy as np
import pandas as pdfrom pyecharts import options as opts
from pyecharts.charts import Geo
from pyecharts.datasets import register_url
from pyecharts.globals import ChartType, SymbolTypedef tsp_by_aco(D):# 城市数量city_cnt = D.shape[0]# 蚂蚁数量ant_cnt = 100# 迭代次数max_iter = 200# 信息素权重系数alpha = 1# 启发信息权重系数beta = 2# 信息素挥发速度rho = 0.1# 城市间球面距离distance = np.zeros((city_cnt, city_cnt))for i in range(city_cnt):for j in range(city_cnt):if i == j:# 相同城市不允许访问distance[i][j] = 1000000else:# 单位：kmdistance[i][j] = 6378.14 * math.acos(math.cos(D[i][1]) * math.cos(D[j][1]) * math.cos(D[i][0] - D[j][0]) +math.sin(D[i][1]) * math.sin(D[j][1]))# 启发信息，距离倒数eta = 1 / distance# 信息素矩阵tau = np.ones((city_cnt, city_cnt))# 每一代最优解generation_best_y = []generation_best_x = []# 种群population = np.zeros((ant_cnt, city_cnt)).astype(int)# 循环迭代for i in range(max_iter):# 城市转移概率prob_matrix = (tau ** alpha) * (eta ** beta)# TSP距离y = np.zeros((ant_cnt, 1))# 依次遍历每只蚂蚁for j in range(ant_cnt):# 设置TSP初始点为0population[j, 0] = 0# 选择后续城市for k in range(city_cnt - 1):# 已访问城市visit = set(population[j, :k + 1])# 未访问城市un_visit = list(set(range(city_cnt)) - visit)# 未访问城市转移概率归一化prob = prob_matrix[population[j, k], un_visit]prob = prob / prob.sum()# 轮盘赌策略选择下个城市next_point = np.random.choice(un_visit, size=1, p=prob)[0]# 添加被选择的城市population[j, k + 1] = next_point# 更新TSP距离y[j] += distance[population[j, k], population[j, k + 1]]# 更新TSP距离：最后一个城市->第0个城市y[j] += distance[population[j, -1], 0]# 保存当前代最优解best_index = y.argmin()generation_best_x.append(population[best_index, :])generation_best_y.append(y[best_index, :])# 计算信息素改变量，ACS模型，Q=1delta_tau = np.zeros((city_cnt, city_cnt))for j in range(ant_cnt):for k in range(city_cnt - 1):delta_tau[population[j, k], population[j, k + 1]] += 1 / y[j]delta_tau[population[j, city_cnt - 1], population[j, 0]] += 1 / y[j]# 信息素更新tau = (1 - rho) * tau + delta_tauprint('iter: {}, best_f: {}'.format(i, generation_best_y[-1]))# 最优解位置best_generation_index = np.array(generation_best_y).argmin()return generation_best_x[best_generation_index], generation_best_y[best_generation_index]def plot_tsp(cities):try:register_url("https://echarts-maps.github.io/echarts-countries-js/")except Exception:import sslssl._create_default_https_context = ssl._create_unverified_contextregister_url("https://echarts-maps.github.io/echarts-countries-js/")'''https://echarts-maps.github.io/echarts-countries-js/preview.html这个网站上显示的各个国家中文名称， 可以写在下面的maptype里面'''title1 = "中国主要城市TSP_by_ACO"c = (Geo().add_schema(maptype='china',  # 可以输入国家名字，比如"瑞士"itemstyle_opts=opts.ItemStyleOpts(color='#323c48', border_color='#111'), )  # 设置地图颜色和边框色)for i in range(len(cities)):c.add("城市",  # 第一个add数据的标题[(cities['城市'].iloc[i], i)],type_=ChartType.EFFECT_SCATTER,  # 使用点的样式，并设置点的颜色，点的大小都是一样的！symbol_size=6,  # 设置点的大小color='red', )  # 点的颜色for i in range(len(cities) - 1):c.add("tsp路线",[(cities['城市'].iloc[i], cities['城市'].iloc[i + 1])],  # 城市顺序type_=ChartType.LINES,effect_opts=opts.EffectOpts(symbol=SymbolType.ARROW, symbol_size=6, color='yellow'),  # 线上的小箭头的颜色linestyle_opts=opts.LineStyleOpts(curve=0.2))  # 设置两点间线缆的弯曲度c.set_series_opts(label_opts=opts.LabelOpts(is_show=False))c.set_global_opts(title_opts=opts.TitleOpts(title=title1),toolbox_opts=opts.ToolboxOpts())c.render('tsp_solution_by_aco.html')if __name__ == '__main__':# 城市及其经纬度original_cities = [['西宁', 101.74, 36.56],['兰州', 103.73, 36.03],['银川', 106.27, 38.47],['西安', 108.95, 34.27],['郑州', 113.65, 34.76],['济南', 117, 36.65],['石家庄', 114.48, 38.03],['太原', 112.53, 37.87],['呼和浩特', 111.65, 40.82],['北京', 116.407526, 39.90403],['天津', 117.200983, 39.084158],['沈阳', 123.38, 41.8],['长春', 125.35, 43.88],['哈尔滨', 126.63, 45.75],['上海', 121.473701, 31.230416],['杭州', 120.19, 30.26],['南京', 118.78, 32.04],['合肥', 117.27, 31.86],['武汉', 114.31, 30.52],['长沙', 113, 28.21],['南昌', 115.89, 28.68],['福州', 119.3, 26.08],['台北', 121.3, 25.03],['香港', 114.173355, 22.320048],['澳门', 113.54909, 22.198951],['广州', 113.23, 23.16],['海口', 110.35, 20.02],['南宁', 108.33, 22.84],['贵阳', 106.71, 26.57],['重庆', 106.551556, 29.563009],['成都', 104.06, 30.67],['昆明', 102.73, 25.04],['拉萨', 91.11, 29.97],['乌鲁木齐', 87.68, 43.77]]original_cities = pd.DataFrame(original_cities, columns=['城市', '经度', '纬度'])# 使用ACO算法求解TSPtime0 = time.time()best_x, best_y = tsp_by_aco(original_cities[['经度', '纬度']].values * math.pi / 180)print('使用ACO求解TSP，耗时: {} s'.format(time.time() - time0))# 按最优解顺序，生成访问城市次序original_cities['seq'] = best_xsort_cities = original_cities.sort_values(by='seq')sort_cities.loc[len(sort_cities)] = sort_cities.loc[0]# 绘制TSP路径plot_tsp(sort_cities)

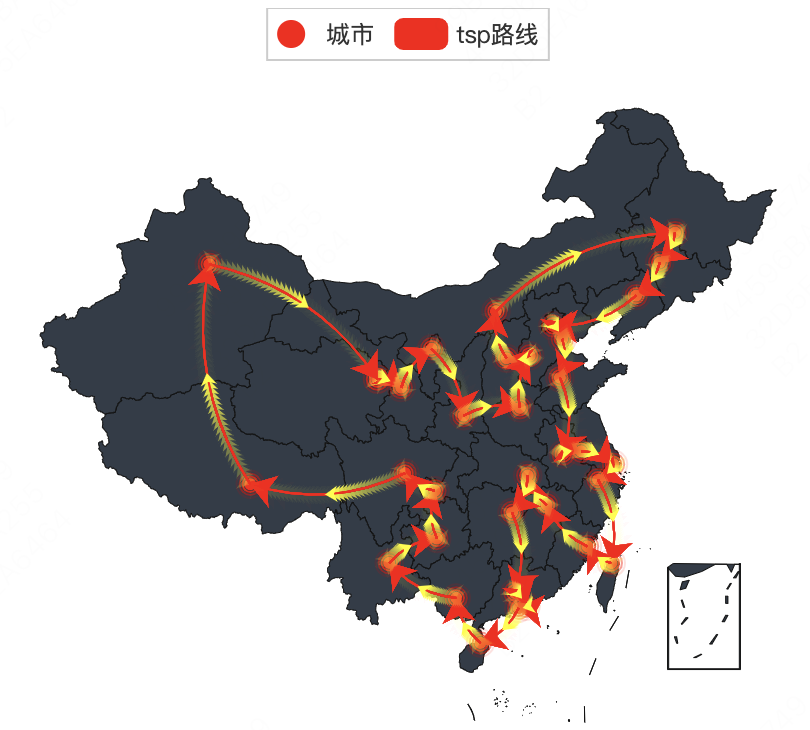
运行代码后，能够得到一个网页版的动图，可以表示运行的轨迹，这里截取了一帧如下。算法输出的最短路径是15944.43815449，从图里其实也能看出来，这个解应该不是全局最优解。需要说明的是，每次运行的结果大概率是不一样的，所以如果大家复跑了这段代码，最优解的值和图的形状不一样是正常的。

整数规划求解TSP

之前的文章里介绍过整数规划可以求解全局最优解，所以本节再用这个方法解一遍TSP，然后把全局最优解拿来和ACO算法的结果做一下对比。TSP问题的整数规划建模不是本文重点，这里就不多描述了，有兴趣的可以参考：优化│TSP中两种不同消除子环路的方法及callback实现（Python调用Gurobi求解）。这里直接给出使用ortools求解模型的代码。

import pandas as pd
import math
import numpy as np
import time
from ortools.linear_solver import pywraplpfrom pyecharts import options as opts
from pyecharts.charts import Geo
from pyecharts.datasets import register_url
from pyecharts.globals import ChartType, SymbolTypedef calc_by_ortools(data):# 生成ortools求解器，使用SCIP算法solver = pywraplp.Solver.CreateSolver('SCIP')# 优化变量x = {}u = {}for i in range(len(data)):u[i] = solver.NumVar(0, solver.infinity(), 'u[%i]' % i)for j in range(len(data)):x[i, j] = solver.IntVar(0, 1, 'x[%i,%i]' % (i, j))# 目标函数:obj_expr = [data[i][j] * x[i, j] for i in range(len(data)) for j in range(len(data))]solver.Minimize(solver.Sum(obj_expr))# 约束条件一: 出度为1for i in range(len(data)):constraint_expr = [x[i, j] for j in range(len(data))]solver.Add(solver.Sum(constraint_expr) == 1)# 约束条件二: 入度为1for j in range(len(data)):constraint_expr = [x[i, j] for i in range(len(data))]solver.Add(solver.Sum(constraint_expr) == 1)# 约束条件三: 消除子环for i in range(1, len(data)):for j in range(1, len(data)):if i != j:solver.Add(u[i] - u[j] + len(data) * x[i, j] <= len(data) - 1)# 模型求解status = solver.Solve()# 模型求解成功, 打印结果if status == pywraplp.Solver.OPTIMAL:# 最优目标函数值print('best_f =', solver.Objective().Value())# 最优次序cnt = 0print(0, end=' ')k = 0best_x = [0]while cnt < len(data):for j in range(len(data)):if x[k, j].solution_value() == 0:continueprint('->', j, end=' ')k = jcnt += 1best_x.append(j)breakprint('\n')return best_xelse:print('not converge.')return []def plot_optimal_routes(cities):try:register_url("https://echarts-maps.github.io/echarts-countries-js/")except Exception:import sslssl._create_default_https_context = ssl._create_unverified_contextregister_url("https://echarts-maps.github.io/echarts-countries-js/")'''https://echarts-maps.github.io/echarts-countries-js/preview.html这个网站上显示的各个国家中文名称， 可以写在下面的maptype里面'''title1 = "中国主要城市TSP_by_ortools"c = (Geo().add_schema(maptype='china',  # 可以输入国家名字，比如"瑞士"itemstyle_opts=opts.ItemStyleOpts(color='#323c48', border_color='#111'), )  # 设置地图颜色和边框色)for i in range(len(cities)):c.add("城市",  # 第一个add数据的标题[(cities['城市'].iloc[i], i)],type_=ChartType.EFFECT_SCATTER,  # 使用点的样式，并设置点的颜色，点的大小都是一样的！symbol_size=6,  # 设置点的大小color='red', )  # 点的颜色for i in range(len(cities) - 1):c.add("tsp路线",[(cities['城市'].iloc[i], cities['城市'].iloc[i + 1])],  # 城市顺序type_=ChartType.LINES,effect_opts=opts.EffectOpts(symbol=SymbolType.ARROW, symbol_size=6, color='yellow'),  # 线上的小箭头的颜色linestyle_opts=opts.LineStyleOpts(curve=0.2))  # 设置两点间线缆的弯曲度c.set_series_opts(label_opts=opts.LabelOpts(is_show=False))c.set_global_opts(title_opts=opts.TitleOpts(title=title1),toolbox_opts=opts.ToolboxOpts())c.render('tsp_solution_by_ortools.html')if __name__ == '__main__':# 城市及其经纬度original_cities = [['西宁', 101.74, 36.56],['兰州', 103.73, 36.03],['银川', 106.27, 38.47],['西安', 108.95, 34.27],['郑州', 113.65, 34.76],['济南', 117, 36.65],['石家庄', 114.48, 38.03],['太原', 112.53, 37.87],['呼和浩特', 111.65, 40.82],['北京', 116.407526, 39.90403],['天津', 117.200983, 39.084158],['沈阳', 123.38, 41.8],['长春', 125.35, 43.88],['哈尔滨', 126.63, 45.75],['上海', 121.473701, 31.230416],['杭州', 120.19, 30.26],['南京', 118.78, 32.04],['合肥', 117.27, 31.86],['武汉', 114.31, 30.52],['长沙', 113, 28.21],['南昌', 115.89, 28.68],['福州', 119.3, 26.08],['台北', 121.3, 25.03],['香港', 114.173355, 22.320048],['澳门', 113.54909, 22.198951],['广州', 113.23, 23.16],['海口', 110.35, 20.02],['南宁', 108.33, 22.84],['贵阳', 106.71, 26.57],['重庆', 106.551556, 29.563009],['成都', 104.06, 30.67],['昆明', 102.73, 25.04],['拉萨', 91.11, 29.97],['乌鲁木齐', 87.68, 43.77]]original_cities = pd.DataFrame(original_cities, columns=['城市', '经度', '纬度'])D = original_cities[['经度', '纬度']].values * math.pi / 180# 城市间球面距离city_distance = np.zeros((len(original_cities), len(original_cities)))for i in range(len(original_cities)):for j in range(len(original_cities)):if i == j:city_distance[i][j] = 100000else:city_distance[i][j] = 6378.14 * math.acos(math.cos(D[i][1]) * math.cos(D[j][1]) * math.cos(D[i][0] - D[j][0]) +math.sin(D[i][1]) * math.sin(D[j][1]))# 使用整数规划求解TSPtime0 = time.time()best_x = calc_by_ortools(city_distance)print('使用ortools求解TSP，耗时: {} s'.format(time.time() - time0))# 绘制TSP路径if len(best_x) > 0:best_routes = []for i in range(len(best_x)):best_routes.append(original_cities['城市'].iloc[best_x[i]])best_routes = pd.DataFrame(best_routes, columns=['城市'])plot_optimal_routes(best_routes)

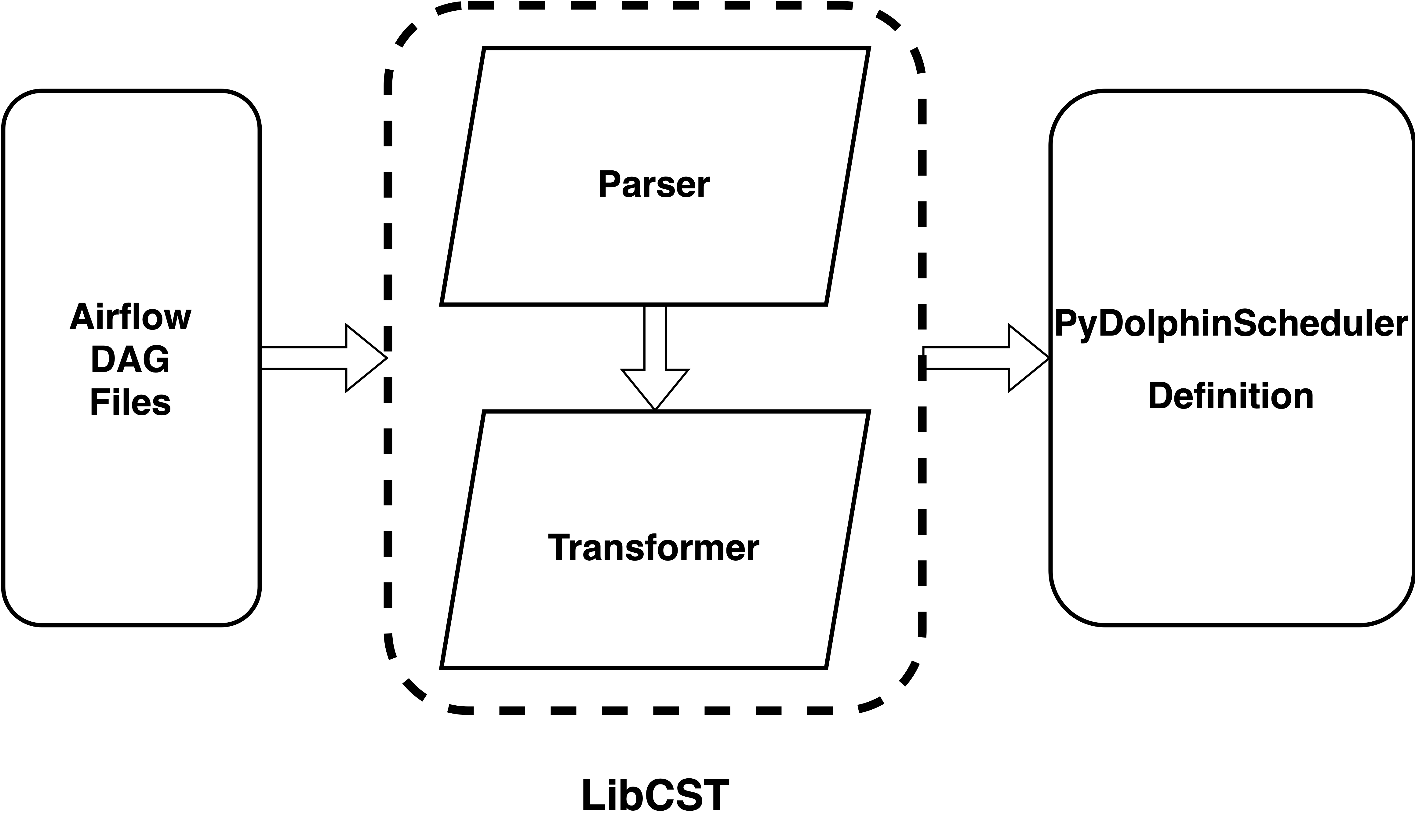
运行程序后，得到最优解为15614.849985682848，可视化路径如下图所示，这个图里的路径看上去更符合我们对全局最优解的认知。相比之下，蚁群算法的结果距离最优解的GAP差不多是2%，看起来也没差那么多。

best_f = 15614.849985682848
0 -> 1 -> 2 -> 3 -> 4 -> 6 -> 7 -> 8 -> 13 -> 12 -> 11 -> 9 -> 10 -> 5 -> 17 -> 16 -> 14 -> 15 -> 22 -> 21 -> 20 -> 18 -> 19 -> 25 -> 23 -> 24 -> 26 -> 27 -> 31 -> 28 -> 29 -> 30 -> 32 -> 33 -> 0 
使用ortools求解TSP，耗时: 88.28608894348145 s