---

🎈 作者：Linux猿

🎈 简介：CSDN博客专家🏆，华为云享专家🏆，Linux、C/C++、云计算、物联网、面试、刷题、算法尽管咨询我，关注我，有问题私聊！

🎈 欢迎小伙伴们点赞👍、收藏⭐、留言💬

---

本文是《动手深度学习》线性回归简洁实现实例的实现和分析，主要对代码进行详细讲解，有问题欢迎在评论区讨论交流。

一、代码实现

实现代码如下所示。

import torch
from torch.utils import data
# d2l包是李沐老师等人开发的动手深度学习配套的包,
# 里面封装了很多有关与数据集定义，数据预处理，优化损失函数的包
from d2l import torch as d2l
# nn 是神经网络 Neural Network 的缩写，提供了一系列的模块和类，实现创建、训练、保存、恢复神经网络
from torch import nn'''
1. 生成数据集，共 1000 条
true_w 和 true_b 是临时变量用于生成数据集
生成 X, y ：满足关系 y = Xw + b + noise
'''
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)'''
2. 构造循环读取数据集的迭代器
'''
def load_array(data_arrays, batch_size, is_train=True):  #@save# 构造一个 PyTorch 数据迭代器，对 tensor 进行打包，包装成 dataset。dataset = data.TensorDataset(*data_arrays)# 根据数据集构造一个迭代器return data.DataLoader(dataset, batch_size, shuffle=is_train)# 小批量数据
batch_size = 10
# 设置了一个数据读取的迭代器，每次读取 batch_size(10) 条
data_iter = load_array((features, labels), batch_size)'''
3. 设置全连接层
'''
'''
# nn.Linear(in_features, out_features, bias=True)
# in_features : 输入向量的列数
# out_features : 输出向量的列数
# bias = True 是否包含偏置
执行线性变换：Yn*o = Xn*i Wi*o + b
其中：W 和 b 模型需要学习的参数
在本例中：n = 10，i = 2, o = 1
'''
net = nn.Sequential(nn.Linear(2, 1))
# 设置权重 w 和 偏置 b
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)'''
4. 定义损失函数
'''
# 均方误差，是预测值与真实值之差的平方和的平均值
loss = nn.MSELoss()
# lr 学习率 learning rate
trainer = torch.optim.SGD(net.parameters(), lr=0.03)'''
4. 训练数据
'''
# 超参数 设置批次
num_epochs = 3
for epoch in range(num_epochs): # 进行 num_epochs 个迭代周期for X, y in data_iter:l = loss(net(X) ,y) # 计算损失，net(X) 计算预测值 y1，loss(y1, y) 计算预测值和真实值之间的差距trainer.zero_grad() # 将所有模型参数的梯度置为 0l.backward() # 求梯度，不使用从零实现中 l.sum.backward 的原因是损失计算中使用了平均的 gardtrainer.step() # 优化参数 w 和 bl = loss(net(features), labels)print(f'epoch {epoch + 1}, loss {l:f}')w = net[0].weight.data
print('w的估计误差：', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差：', true_b - b)

二、实现解析

针对实例中重要的函数解析如下。

2.1 Linear 函数

nn.Linear(in_features, out_features, bias=True)

神经网络的线性层，也成为全连接层，进行 Y = XW + b 的线性变换。

参数：

in_features : 输入向量的列数

out_features : 输出向量的列数

bias = True 是否包含偏置

in_features 和 out_features 是 W 的行和列。

执行线性变换：Yn*o = Xn*i Wi*o + b

其中：W 和 b 模型需要学习的参数

在本例中：n = 10，i = 2, o = 1。

2.2 Sequential 函数

一个序列容器，用于搭建神经网络的模块，按照传入构造器的顺序添加到 nn.Sequential() 容器中。按照内部模块的顺序自动依次计算并输出结果。

2.3 MSELoss 函数

均方误差，是预测值与真实值之差的平方和的平均值，即：

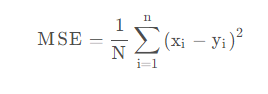
2.4 TensorDataset 函数

用来对 tensor 进行打包，就好像 python 中的 zip 功能。该类通过每一个 tensor 的第一个维度进行索引。因此，该类中的 tensor 第一维度必须相等. 另外：TensorDataset 中的参数必须是 tensor。可以参考如下例子：

import torch
from torch.utils.data import TensorDataset
from torch.utils.data import DataLoader# len = 12
a = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9], [1, 2, 3], [4, 5, 6], [7, 8, 9], [1, 2, 3], [4, 5, 6], [7, 8, 9], [1, 2, 3], [4, 5, 6], [7, 8, 9]])
# len = 12
b = torch.tensor([44, 55, 66, 44, 55, 66, 44, 55, 66, 44, 55, 66])
# 将 tensor a 和 b 压缩在一起
train_ids = TensorDataset(a, b)
# 输出
for x, y in train_ids:print(x, y)

输出如下：

tensor([1, 2, 3]) tensor(44)
tensor([4, 5, 6]) tensor(55)
tensor([7, 8, 9]) tensor(66)
tensor([1, 2, 3]) tensor(44)
tensor([4, 5, 6]) tensor(55)
tensor([7, 8, 9]) tensor(66)
tensor([1, 2, 3]) tensor(44)
tensor([4, 5, 6]) tensor(55)
tensor([7, 8, 9]) tensor(66)
tensor([1, 2, 3]) tensor(44)
tensor([4, 5, 6]) tensor(55)
tensor([7, 8, 9]) tensor(66)

2.5 DataLoader 函数

DataLoader 是用来包装所使用的数据，每次抛出一批数据，下面来看一个例子。

import torch
from torch.utils import data# len = 12
a = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9], [1, 2, 3], [4, 5, 6], [7, 8, 9], [1, 2, 3], [4, 5, 6], [7, 8, 9], [1, 2, 3], [4, 5, 6], [7, 8, 9]])
# len = 12
b = torch.tensor([44, 55, 66, 44, 55, 66, 44, 55, 66, 44, 55, 66])
# 将 tensor a 和 b 压缩在一起
train_ids = data.TensorDataset(a, b)
# 输出
#for x, y in train_ids:
#    print(x, y)BATCH_SIZE = 4
loader = data.DataLoader(dataset=train_ids,batch_size=BATCH_SIZE, # 每次取 BATCH_SIZE=4 个数据shuffle=False, # 不打乱顺序,便于查看num_workers=0)for x, y in loader:print(x, y)break

输出如下：

tensor([[1, 2, 3],[4, 5, 6],[7, 8, 9],[1, 2, 3]]) tensor([44, 55, 66, 44])

 如上所示，输出第一个 BATCH_SIZE=4。

2.6 zero_grad 函数

trainer.zero_grad() 是用来清空模型参数梯度的函数，它将模型参数的梯度缓存设置为 0。在进行反向传播时，梯度会累加，如果不清空梯度，会影响后续的梯度计算。

2.7 backward 函数

对计算图进行梯度计算，求解计算图中所有节点的梯度。

2.8 step 函数

根据 backward 函数计算出的梯度进行参数更新。

参考链接：

线性回归的实现学习_data.tensordataset_带刺的厚崽的博客-CSDN博客

nn.Sequential()_一颗磐石的博客-CSDN博客

【Pytorch基础】torch.nn.MSELoss损失函数_一穷二白到年薪百万的博客-CSDN博客

pytorch之trainer.zero_grad()_FibonacciCode的博客-CSDN博客

清空模型参数梯度的函数 - 知乎

pytorch中backward()函数详解_backward函数_Camlin_Z的博客-CSDN博客

理解Pytorch的loss.backward()和optimizer.step() - 知乎

---

🎈 感觉有帮助记得「一键三连」支持下哦！有问题可在评论区留言💬，感谢大家的一路支持！🤞猿哥将持续输出「优质文章」回馈大家！🤞🌹🌹🌹🌹🌹🌹🤞

---