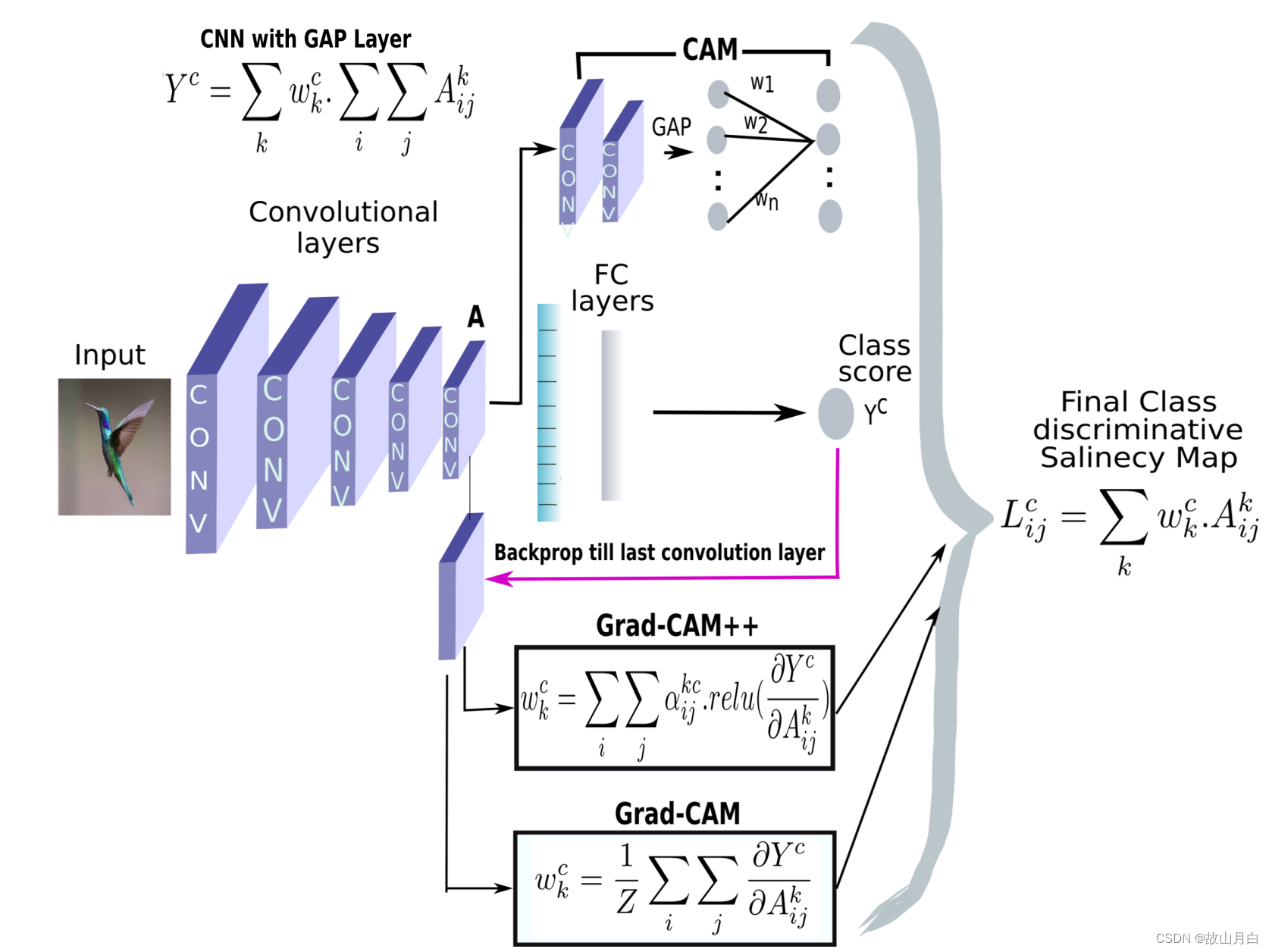
平面波向球面波的展开

平面波向球面波的展开是一个极其重要的话题

$e^{-i\vec{k}\cdot\vec{r}}=e^{-ikrcos\theta}=e^{-ikrx}=\sum_{l=0}^\infty c_l(kr)P_l(x)$

手稿放在文章的结尾处

勒让德展开

$\int_{-1}^1e^{-ikrx}P_l(x)dx=c_l(kr)\int_{-1}^1P^2_l(x)dx$

citation 1:

$\int_{-1}^1P_l^2(x)dx=\frac{2}{2l+1}$

我们整理一下，对exp(x)做泰勒展开，得

$c_l(kr)=\sum_{n=0}^\infty \frac{(-i)^n(kr)^n}{n!}\int_{-1}^1x^nP_l(x)dx$

citation 2:

$P_l(x)=\frac{1}{2^ll!}\frac{d^l}{dx^l}(x^2-1)^l$

我们先把精力集中到解决这个积分上去
- 反复利用分部积分

$\int_{-1}^{1}x^n\frac{d^l}{dx^l}(x^2-1)^l dx=[x^n\frac{d^{l-1}}{dx^{l-1}}(x^2-1)|^{1}_{-1}-n\int_{-1}^1x^{n-1}(x^2-1)^ldx]=...$

$=(-1)^n\frac{n!}{(n-l)!}\int_{-1}^1x^{n-1}(x^2-1)^ldx$

考虑到奇偶性问题
- 当且仅当 $n=2m+l$ 时积分不为零
现在做变换
- 注意，这是一个偶函数积分，因此我们只需要计算0-1上的积分然后乘2

$=\frac{n!}{(2m)!}\int_0^1t^{m-1/2}(t-1)^ldt$

citation 3:B函数
- 对于B函数我们需要知道的不多，只需要知道

$\int_0^1t^{m-1}(t-1)^{n-1}dt=B(m,n)=\frac{\Gamma(m)\Gamma(n)}{\Gamma(m+n)}$

很好，现在我们回到主线上去
- 经过一些小小的整理，我们可以得到

$c_l(kr)=\frac{2l+1}{2\times 2^{l}}(-i)^l\sum_{m=0}^\infty \frac{(-1)^m\times(kr)^{2m+l}}{(2m)!}\frac{\Gamma(m+1/2)}{\Gamma(m+l+3/2)}$

现在分离出一个 $\Gamma(1/2)$ 出来

$c_l(kr)=\frac{2l+1}{2\times 2^{l}}(-i)^l\sum_{m=0}^\infty \frac{(-1)^m\times(kr)^{2m+l}}{(2m)!}\frac{\Gamma(1/2)\Gamma(m+1/2)}{\Gamma(1/2)\Gamma(m+l+3/2)}$

citation 4:小技巧
- 证明非常得简单，只需要按照 $\Gamma(z+1)=z\Gamma(z)$ 不断展开即可
citation 5:小技巧
- 证明同样非常得简单

我们最后一次回到主线上去，现在我们已经可以得到了

$(2l+1)(-i)^l\sum_{m=0}^\infty (-1)^m(\frac{kr}{2})^{2m+l}\frac{\Gamma(1/2)}{2\cdot m!\Gamma(m+l+3/2)}$

虽然在特殊函数的课本上没有明确得给出球贝塞尔函数的表达式，但是这对于聪明的我们来说完全没有任何问题

$j_l(z)=\frac{\Gamma(1/2)}{2}\sum_{m=0}^\infty\frac{(-1)^m}{m!\Gamma(m+l+3/2)}(\frac{z}{2})^{2m+l}$

于是我们得到了

$c_l=(2l+1)(-i)^lj_l(kr)$

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/177750.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

平面波向球面波的展开

相关文章

红队专题-从零开始VC++C/S远程控制软件RAT-MFC-远程桌面屏幕监控

解析mfc100u.dll文件丢失的修复方法，快速解决mfc100u.dll问题

精品Python空巢老人志愿服务平台慈善捐赠活动报名

PicoDiagnostics (NVH设备软件)-电脑无法识别示波器（安装驱动）

[Linux 基础] Linux使用git上传gitee三板斧

神经网络的解释方法之CAM、Grad-CAM、Grad-CAM++、LayerCAM

本地创建一个虚拟机，并且能够连接到外网

Flask Shell 操作 SQLite

记录rider编辑器快速文档中英文显示的问题

关于CSS的几种字体悬浮的设置方法

博后像苦力，ChatGPT来助力？nature：博士后三分之一在用GPT帮忙工作

CSS内容过多保留固定字数并显示省略号

C语言 Number 1 基本数据类型

领先实践｜IDEO 最佳设计思维和策略框架

Logstash学习

Louis 谈 Restaking：去中心化信任的交流电时刻

开发板挂载 Ubuntu 的 NFS 目录

聚观早报 |Windows 11重大更新；荣耀双11开门红

解决uniapp的video标签和transition属性使用时出现错位的问题

21款奔驰GLC300L升级23P驾驶辅助出行更加的安全