关于pytorch张量维度转换大全
- 1 tensor.view()
- 2 tensor.reshape()
- 3 tensor.squeeze()和tensor.unsqueeze()
- 3.1 tensor.squeeze() 降维
- 3.2 tensor.unsqueeze(idx)升维
- 4 tensor.permute()
- 5 torch.cat([a,b],dim)
- 6 torch.stack()
- 7 torch.chunk()和torch.split()
- 8 与tensor相乘运算
- 9 与tensor相加运算
- 10 tensor.expand()
- 11 tensor.narrow(dim, start, len)
- 12 tensor.resize_()
- 13 tensor.repeat()
- 14 unbind()
- 参考:
tensor 乘
tensor 加
# view() 转换维度
# reshape() 转换维度
# permute() 坐标系变换
# squeeze()/unsqueeze() 降维/升维
# expand() 扩张张量
# narraw() 缩小张量
# resize_() 重设尺寸
# repeat(), unfold() 重复张量
# cat(), stack() 拼接张量
1 tensor.view()
view() 用于改变张量的形状,但不会改变张量中的元素值。
用法1:
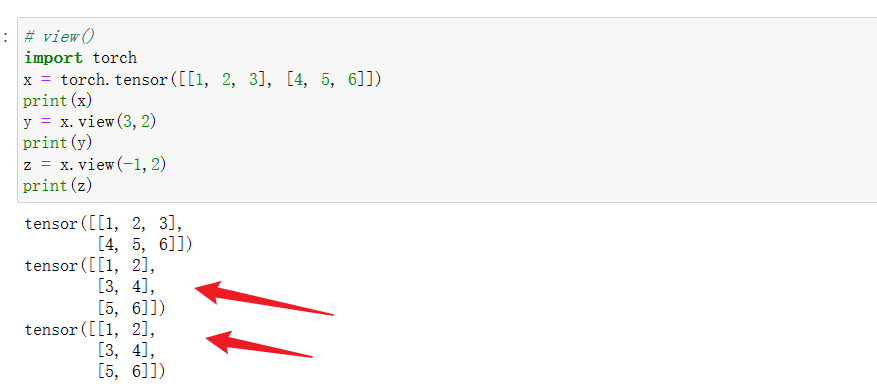
例如,你可以使用view 将一个形状是(2,3)的张量变换成(3,2)的张量;
import torch
x = torch.tensor([[1, 2, 3], [4, 5, 6]])
y = x.view(3, 2)
上面的操作相当于,先把形状为**(2,3)的tensor展平,变成(1,6),然后再变成(3,2).**
用法2:
转换前后张量中的元素个数不变。view()中若存在某一维的维度是-1,则表示该维的维度根据总元素个数和其他维度尺寸自适应调整。注意,view()中最多只能有一个维度的维数设置成-1。
z = x.view(-1,2)
举例子:
在卷积神经网络中,经常会在全连接层用到view进行张量的维度拉伸:
假设输入特征是BCH*W的4维张量,其中B表示batchsize,C表示特征通道数,H和W表示特征的高和宽,在将特征送入全连接层之前,会用.view将转换为B*(CHW)的2维张量,即保持batch不变,但将每个特征转换为一维向量。
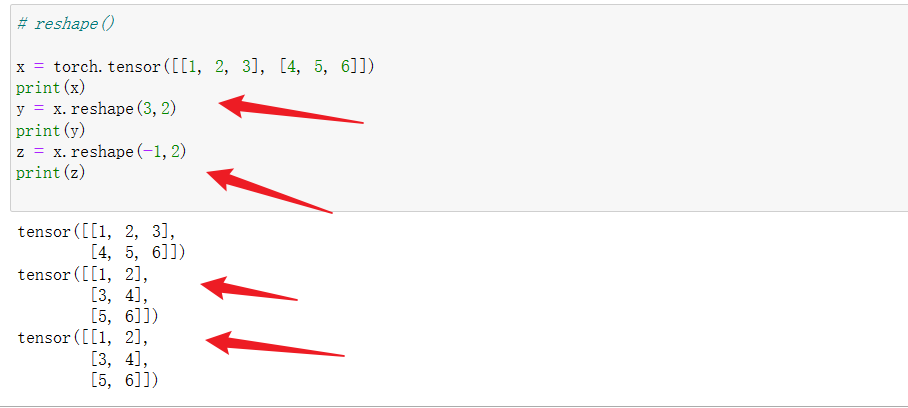
2 tensor.reshape()
reshape()与view()使用方法相同。
3 tensor.squeeze()和tensor.unsqueeze()
3.1 tensor.squeeze() 降维
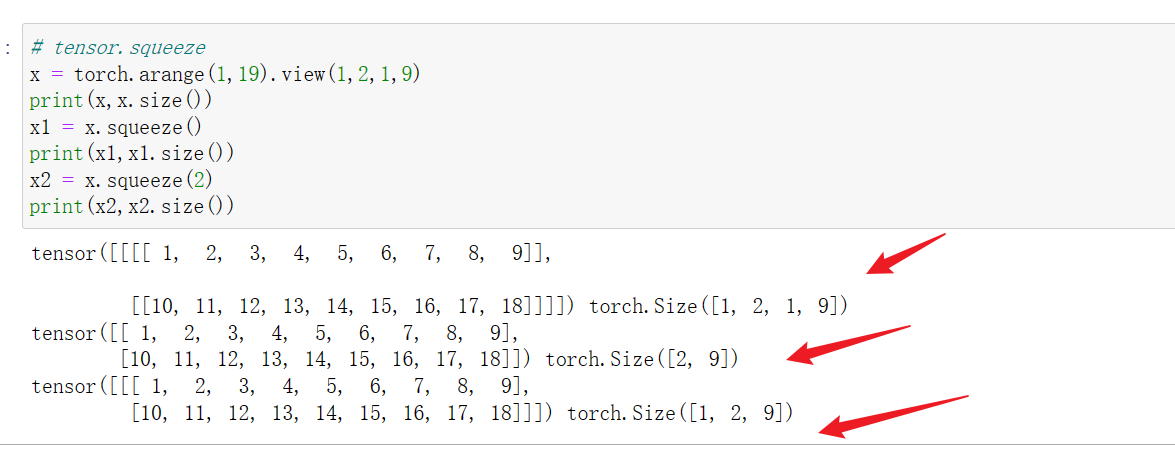
(1)若squeeze()括号内为空,则将张量中所有维度为1的维数进行压缩,如将1,2,1,9的张量降维到2,9维;若维度中无1维的维数,则保持源维度不变,如将234维的张量进行squeeze,则转换后维度不会变。
(2)若squeeze(idx),则将张量中对应的第idx维的维度进行压缩,如1,2,1,9的张量做squeeze(2),则会降维到1,2,9维的张量;若第idx维度的维数不为1,则squeeze后维度不会变化。
例如:
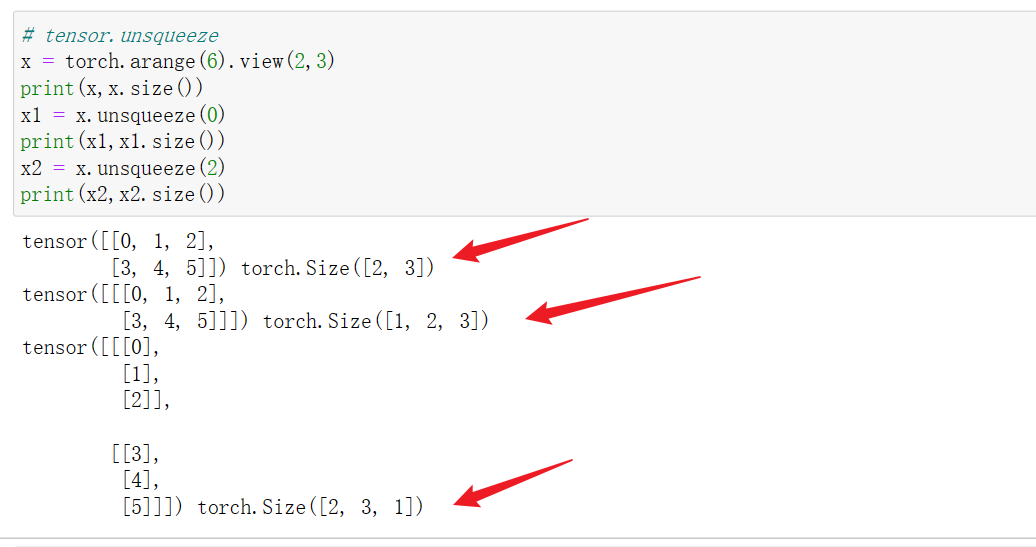
3.2 tensor.unsqueeze(idx)升维
在第idx维进行升维,将tensor由原本的维度n,升维至n+1维。如张量的维度维2*3,经unsqueeze(0)后,变为1,2,3维度的张量。
4 tensor.permute()
坐标系转换,即矩阵转置,使用方法与numpy array的transpose相同。permute()括号内的参数数字指的是各维度的索引值。permute是深度学习中经常需要使用的技巧,一般的会将BCHW的特征张量,通过转置转化为BHWC的特征张量,即将特征深度转换到最后一个维度,通过调用**tensor.permute(0, 2, 3, 1)**实现。
torch.transpose只能操作2D矩阵的转置,而permute()函数可以对任意高维矩阵进行转置;
简单理解:permute()相当于可以同时操作tensor的若干维度,transpose只能同时作用于tensor的两个维度。
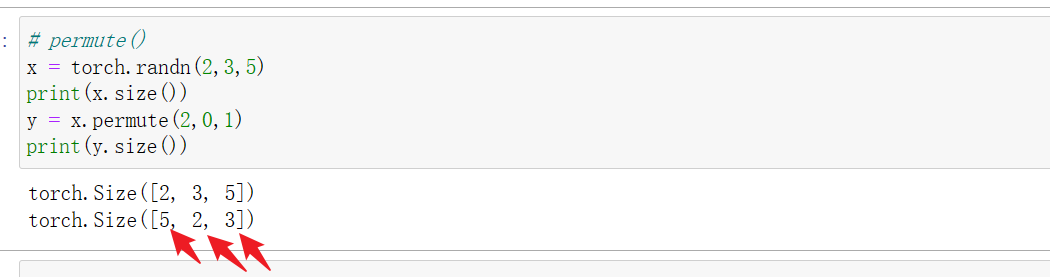
permute和view/reshape虽然都能将张量转化为特定的维度,但原理完全不同,注意区分。view和reshape处理后,张量中元素顺序都不会有变化,而permute转置后元素的排列会发生变化,因为坐标系变化了。
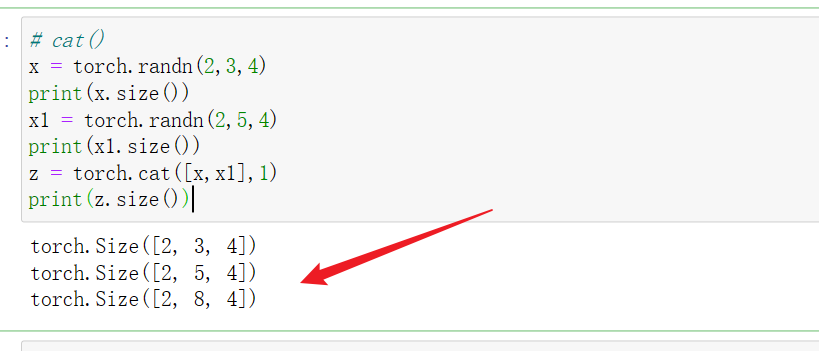
5 torch.cat([a,b],dim)
在第dim维度进行张量拼接,要注意维度保持一致。
假设a为h1w1的二维张量,b为h2w2的二维张量,torch.cat(a,b,0)表示在第一维进行拼接,即在列方向拼接,所以w1和w2必须相等。torch.cat(a,b,1)表示在第二维进行拼接,即在行方向拼接,所以h1和h2必须相等。
假设a为c1h1w1的二维张量,b为c2h2w2的二维张量,torch.cat(a,b,0)表示在第一维进行拼接,即在特征的通道维度进行拼接,其他维度必须保持一致,即w1=w2,h1=h2。torch.cat(a,b,1)表示在第二维进行拼接,即在列方向拼接,必须保证w1=w2,c1=c2;torch.cat(a,b,2)表示在第三维进行拼接,即在行方向拼接,必须保证h1=h2,c1=c2;
6 torch.stack()
该函数在维度上连接若干个形状相同的张量,最终结果会升维;即若干个张量在某一维度上连接生成一个扩维的张量。 堆叠的感觉。

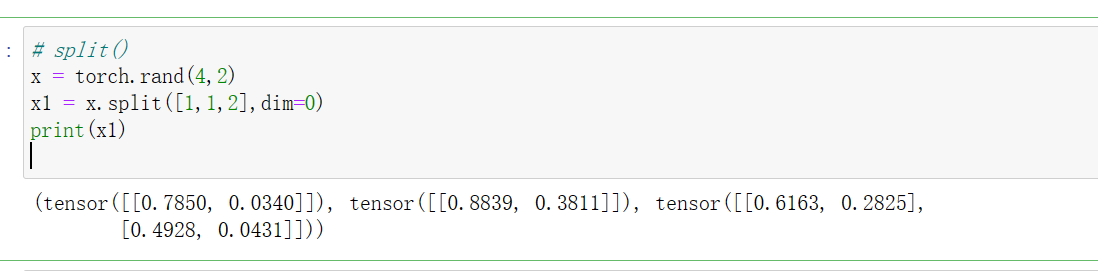
7 torch.chunk()和torch.split()
torch.chunk(input, chunks, dim)
**torch.chunk()**的作用是把一个tensor均匀分成若干个小tensor。input是被分割的tensor。chunks是均匀分割的份数,如果在进行分割的维度上的size不能被chunks整除,则最后一份tensor会略小(也可能为空)。dim是确定在某个维度上进行分割。该函数返回的是由小tensor组成的tuple。

**torch.split()**可以说是torch.chunk()的升级版,它不仅可以按份数均匀分割,还可以按特定的方案进行分割。
torch.split(input, split_size_or_sections, dim=0)
与torch.chunk()的区别就在于第二个参数上面。如果第二个参数是分割份数,这就和torch.chunk()一样了;第二种是分割方案,是一个list类型的数据,待分割的张量将会被分割为len(list)份,每一份的大小取决于list中的元素。
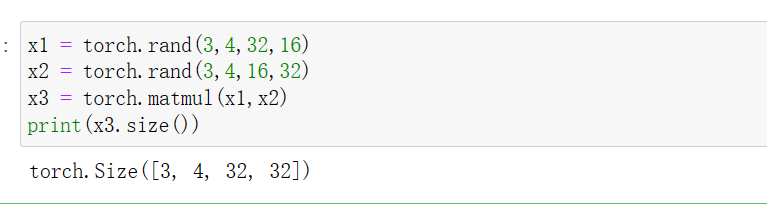
8 与tensor相乘运算
- 元素积(element-wise),即相同形状的矩阵对应元素相乘,得到的元素为结果矩阵中各个元素的值,对应函数为torch.mul()(和*的效果一样)。

- 矩阵乘法,对应函数为torch.mm()(只能用于2d的tensor)或者torch.matmul()(和符号@效果一样)。对于torch.matmul(),定义其矩阵乘法仅在最后的两个维度上,前面的维度需要保持一致。如果前面的维度符合broadcast_tensor机制,也会自动扩展维度,保证两个矩阵前面的维度一致。

9 与tensor相加运算
遵循下面两点:
- 当两个tensor的维度相同时,对应轴的值要一样(每个维度的大小相等),或者某些维度大小为1。相加时把所有为1的轴进行复制扩充得到两个维度完全相同的张量,然后对应位置相加即可。
- 当两个相加的tensor维度不一致时,首先要把维度低的那个张量从右边和维度高的张量对齐,用1扩充维度至和高维度张量的维度一致,然后进行<1>的操作。

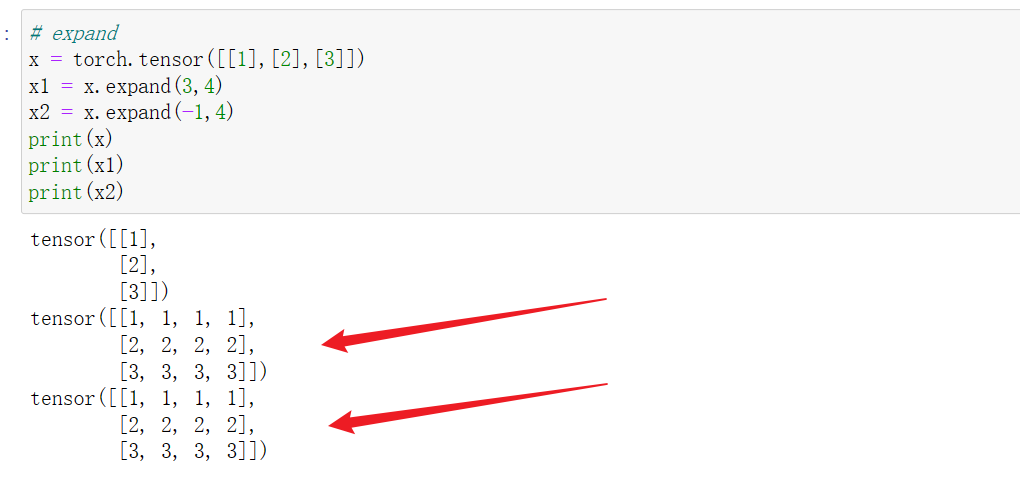
10 tensor.expand()
扩展张量,通过值复制的方式,将单个维度扩大为更大的尺寸。使用expand()函数不会使原tensor改变,需要将结果重新赋值。下面是具体的实例:
以二维张量为例:tensor是1n或n1维的张量,分别调用tensor.expand(s, n)或tensor.expand(n, s)在行方向和列方向进行扩展。
expand()的填入参数是size
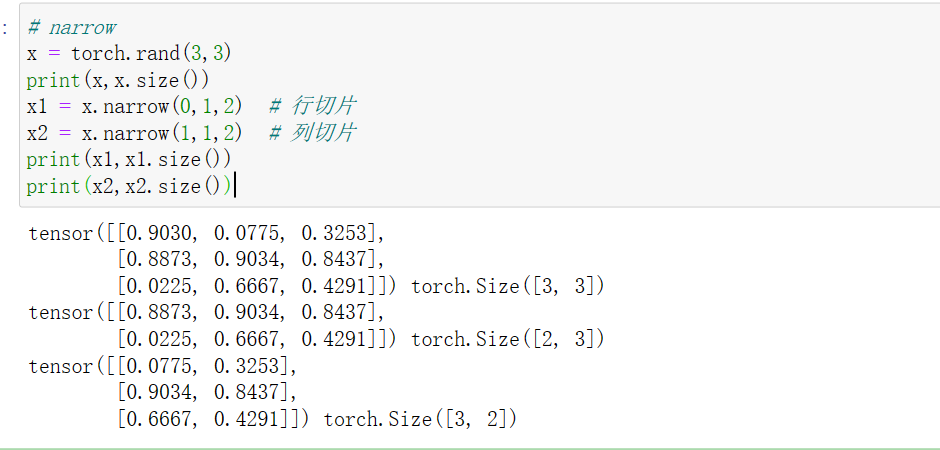
11 tensor.narrow(dim, start, len)
narrow()函数起到了筛选一定维度上的数据作用.
torch.narrow(input, dim, start, length)->Tensor
input是需要切片的张量,dim是切片维度,start是开始的索引,length是切片长度,实际应用如下:
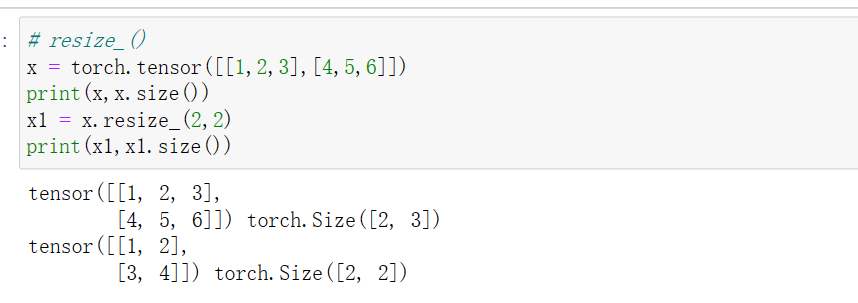
12 tensor.resize_()
尺寸变化,将tensor截断为resize_后的维度.
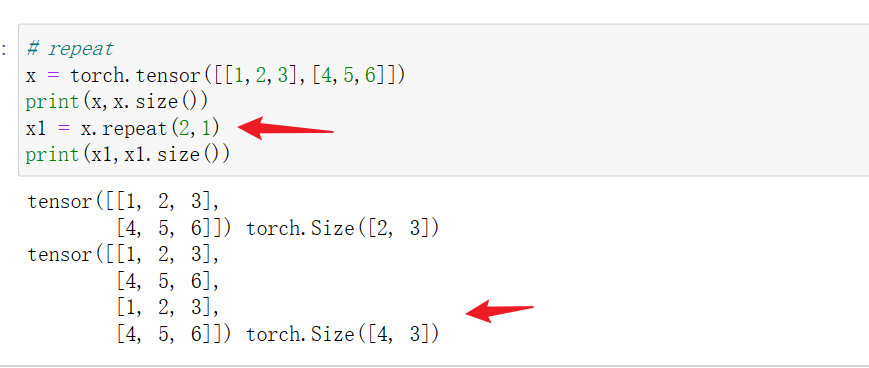
13 tensor.repeat()
tensor.repeat(a,b)将tensor整体在行方向复制a份,在列方向上复制b份
14 unbind()
torch.unbind()移除指定维后,返回一个元组,包含了沿着指定维切片的各个切片。
torch.unbind(input, dim=0)->seq

参考:
pytorch中与tensor维度变化相关的函数(持续更新) - weili21的文章 - 知乎
https://zhuanlan.zhihu.com/p/438099006
【pytorch tensor张量维度转换(tensor维度转换)】
https://blog.csdn.net/x_yan033/article/details/104965077