【数据结构】单链表OJ题

在这里插入图片描述

前言:
本节博客将讲解单链表的反转，合并有序链表，寻找中间节点及约瑟夫问题

文章目录

一、反转链表
二、合并有序链表
三、链表的中间结点
四、环形链表的约瑟夫问题

一、反转链表

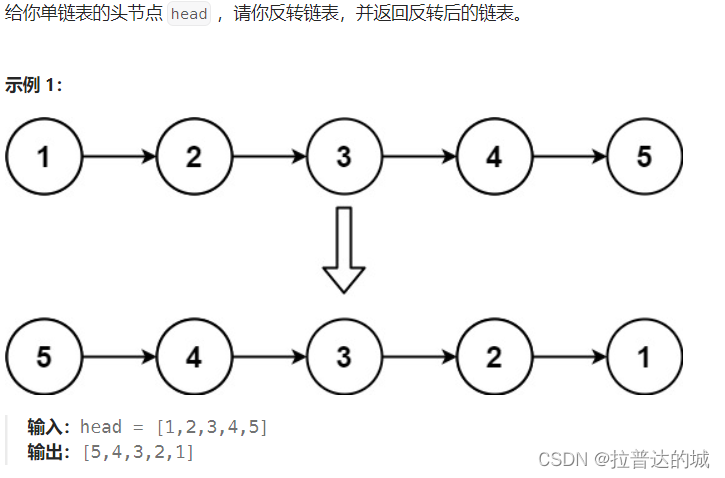
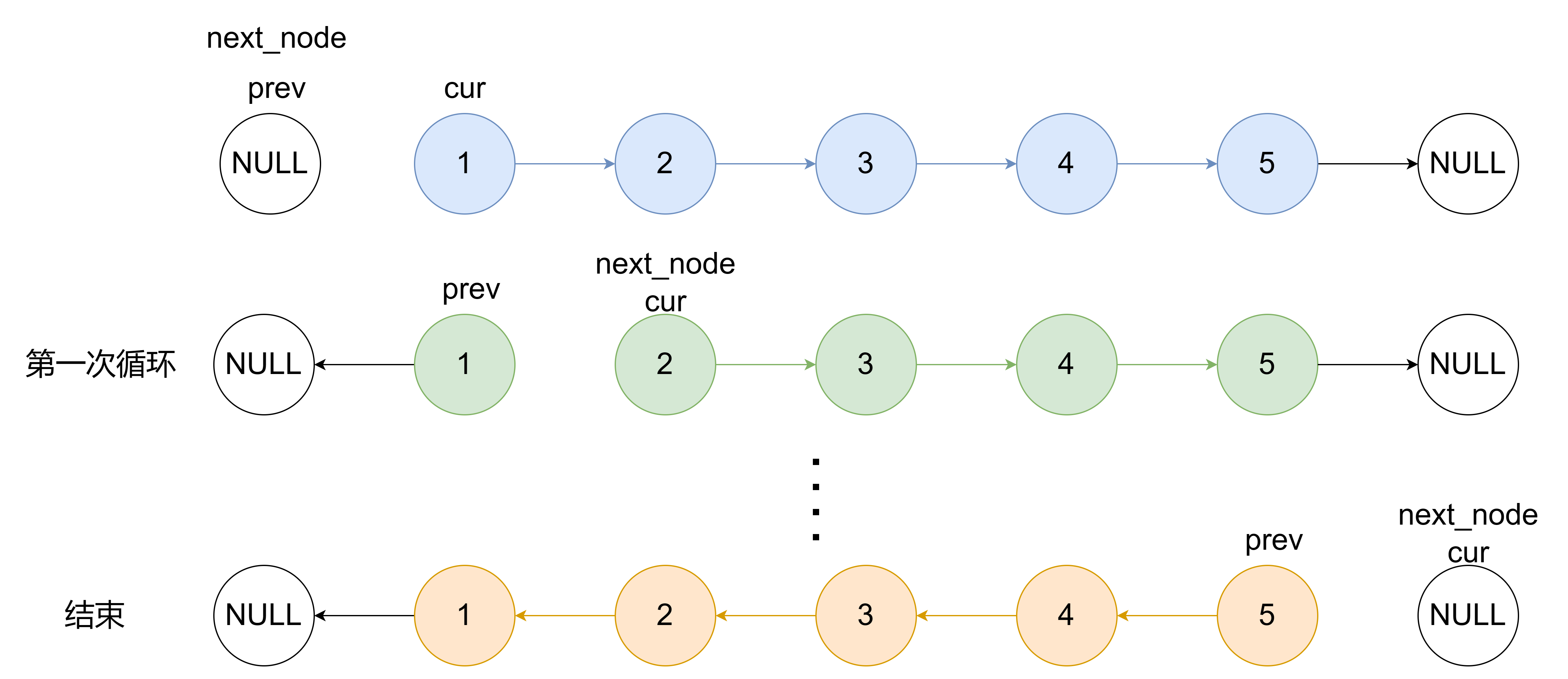
在这里插入图片描述

要反转链表，我们需要遍历链表并改变每个节点的 next 指针，使其指向其前一个节点。为了完成这个任务，我们需要三个指针：prev、cur和 next_node。

prev：保存当前节点的前一个节点。初始化为 NULL，因为链表的新头部（原始链表的尾部）的 next 指针将指向 NULL。
cur：表示当前正在处理的节点。
next_node：保存当前节点的下一个节点。

struct ListNode* reverseList(struct ListNode* head) {typedef struct ListNode ListNode;ListNode* prev = NULL;ListNode* cur = head;ListNode* next_node = NULL;while (cur != NULL) {next_node = cur->next;  // 保存当前节点的下一个节点cur->next = prev;       // 更新当前节点的next指针prev = cur;             // 将prev移动到当前节点cur = next_node;        // 移动到下一个节点}return prev;  // 返回新的头部
}

二、合并有序链表

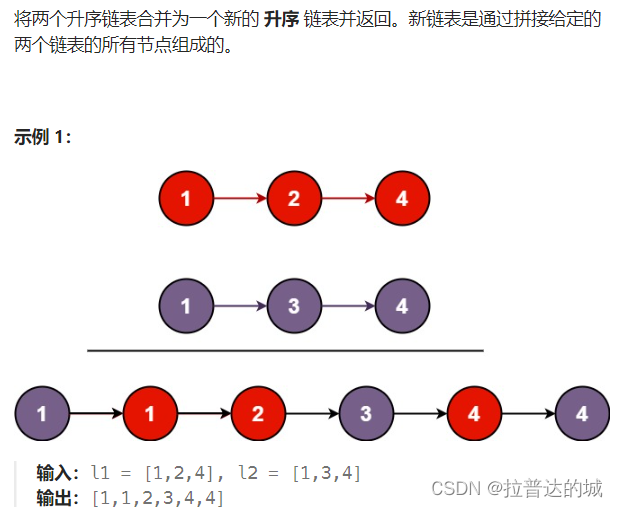
在这里插入图片描述
分为四个步骤：

开始阶段: 首先，函数检查两个列表是否为空。如果其中一个为空，则直接返回另一个列表，因为没有合并的必要。
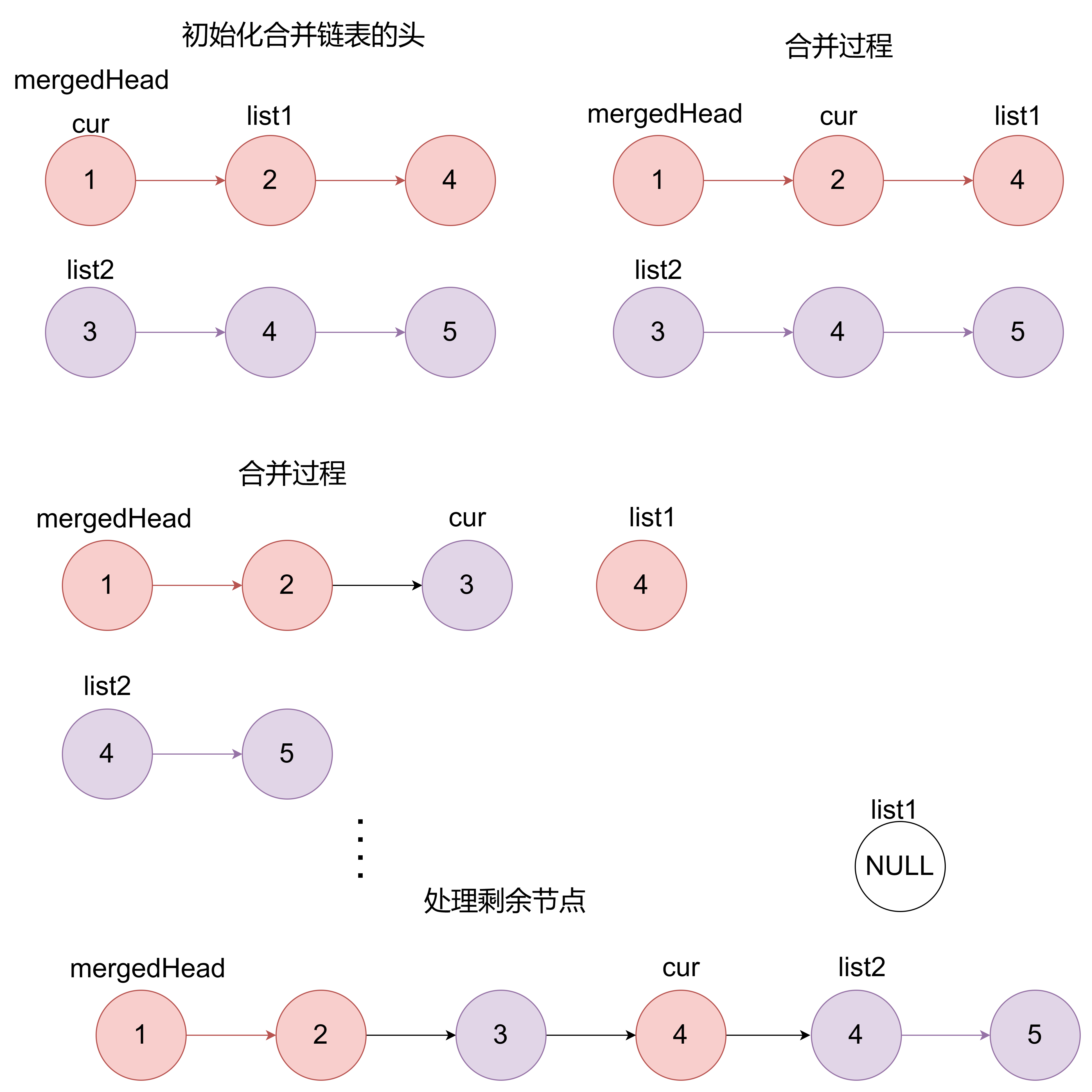
初始化合并链表的头: 函数接着检查list1和list2的首个节点，看哪一个的值较小。较小的那个节点将成为新的合并链表的首个节点。
合并过程: 使用一个while循环来遍历list1和list2，每次循环会从这两个列表中选择一个较小的节点，并将其添加到合并列表的末尾。
处理剩余节点: 循环结束后，list1和list2可能还有未处理的节点。以下的代码将剩余的节点添加到合并列表的末尾。

typedef struct ListNode ListNode;
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2) {//开始阶段if (!list1) return list2;if (!list2) return list1;//初始化合并链表的头ListNode* mergedHead = NULL;  // 合并后的链表头if (list1->val < list2->val) {mergedHead = list1;list1 = list1->next;} else {mergedHead = list2;list2 = list2->next;}ListNode* cur = mergedHead;  // 指向合并后链表的当前节点//合并过程while (list1 && list2) {if (list1->val <= list2->val) {cur->next = list1;list1 = list1->next;} else {cur->next = list2;list2 = list2->next;}cur = cur->next;}//处理剩余节点// 如果list1还有剩余节点if (list1) {cur->next = list1;}// 如果list2还有剩余节点if (list2) {cur->next = list2;}return mergedHead;
}

在这里插入图片描述

三、链表的中间结点

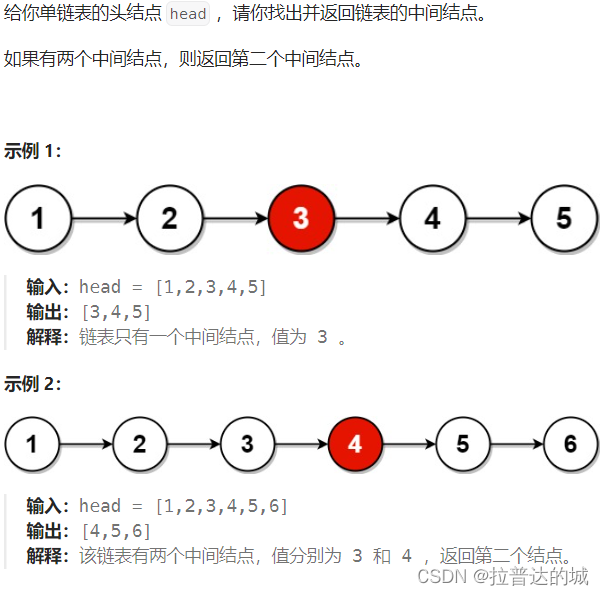
在这里插入图片描述
这题我们可以使用快慢指针，在循环中，fast 指针每次移动两个节点，而 slow 指针每次只移动一个节点。这意味着，当 fast 指针到达链表的末尾时，slow 指针将位于链表的中间位置。

 typedef struct ListNode ListNode;
struct ListNode* middleNode(struct ListNode* head) {ListNode* fast = head;ListNode* slow = head;while(fast && fast->next){slow = slow->next;fast = fast->next->next;}return slow;
}

四、环形链表的约瑟夫问题

在这里插入图片描述
以下是代码的主要思路：

数据结构选择：
使用单向循环链表来模拟这个问题。循环链表是一个适合此问题的数据结构，因为当链表到达末尾时，它可以自动回到头部。
链表节点创建：
ListBuyNode(int x)：这个函数用于创建一个新的链表节点，它接受一个整数值 x 作为参数，并返回一个新的链表节点。
循环链表创建：
CreateList(int n)：这个函数用于创建一个有 n 个节点的单向循环链表。链表的节点值从 1 到 n。链表的最后一个节点指向头节点，使其形成一个循环。
约瑟夫环算法：

ysf(int n, int m)：这个函数实现了约瑟夫环的主要算法。
首先，它调用 CreateList(n) 来创建一个 n 个节点的单向循环链表。
使用两个指针，prev 和 cur，分别表示当前节点的前一个节点和当前节点。
使用一个计数器 count 从 1 开始计数，每次循环增加计数器的值。
当 count 达到 m 时，当前的 cur 节点将被删除（淘汰），并释放其内存。然后，cur 指向下一个节点，并且计数器重置为 1。
如果 count 不等于 m，prev 和 cur 都向前移动一个节点，继续循环。
当链表只剩下一个节点时（即 cur->next 等于 cur 时），循环结束。
返回最后一个剩下的节点的值，即最后一个被淘汰的人的位置。

// 定义链表节点结构
typedef struct ListNode ListNode;// 分配内存并创建一个链表节点，值为x
ListNode* ListBuyNode(int x){ListNode* node = (ListNode*)malloc(sizeof(ListNode)); // 分配内存if(node == NULL){ // 检查内存分配是否成功perror("Malloc fail;");exit(1); // 分配失败，退出程序}node->val = x; // 设置节点的值node->next = NULL; // 初始化下一个节点为NULLreturn node; // 返回创建的节点
}// 创建一个包含n个节点的单向循环链表
ListNode* CreateList(int n){ListNode* phead = ListBuyNode(1); // 创建头节点，值为1ListNode* pTail = phead; // 初始化尾节点为头节点for(int i = 2; i <= n; i++){ // 从2到n循环创建节点ListNode* node = ListBuyNode(i); // 创建新节点pTail->next = node; // 把新节点连接到链表的尾部pTail = pTail->next; // 更新尾节点为新创建的节点}pTail->next = phead; // 将链表的尾部连接到头部，使其成为一个循环链表return pTail; // 返回链表的尾节点
}// 约瑟夫环问题的解决函数
int ysf(int n, int m ) {ListNode* prev = CreateList(n); // 创建一个单向循环链表，并返回尾节点ListNode* cur = prev->next; // 当前节点从头节点开始int count = 1; // 计数器初始化为1while(cur->next != cur){ // 当链表只剩下一个节点时停止循环if(count == m){ // 当计数器达到m时prev->next = cur->next; // 删除当前节点free(cur); // 释放当前节点的内存cur = prev->next; // 更新当前节点为下一个节点count = 1; // 重置计数器}else{prev = cur; // 否则，移动到下一个节点cur = cur->next;count++; // 增加计数器}}return cur->val; // 返回最后剩下的节点的值
}