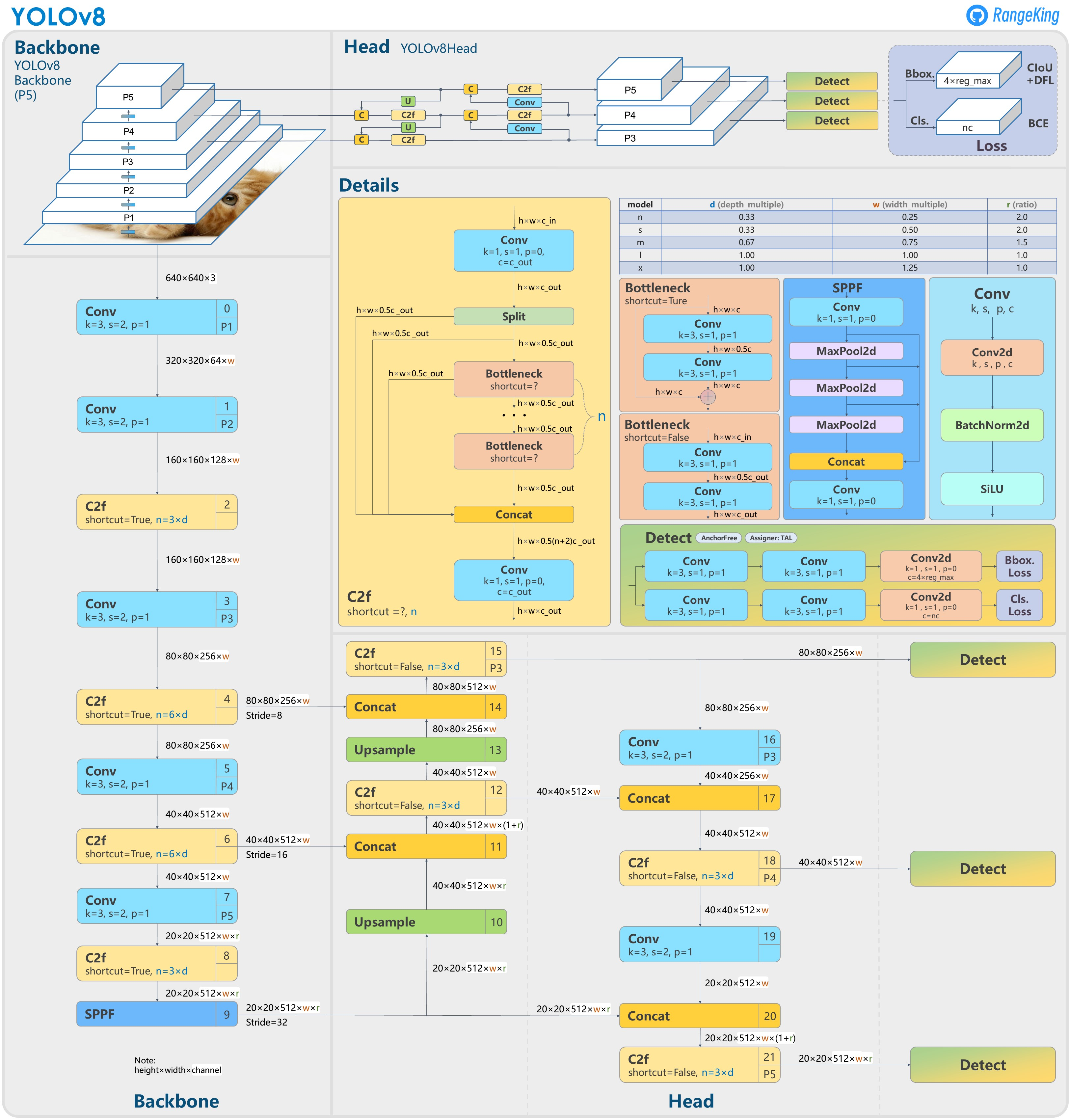
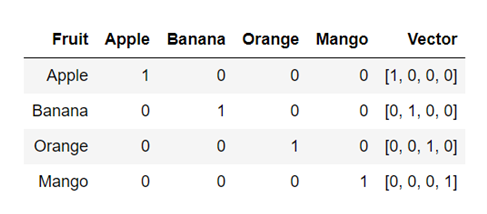
B、5286. 翻倍(思维+推导)
一、题目要求
给定两个正整数,初始时两数均为 1。
你可以进行任意次(也可以不进行)翻倍操作,每次操作任选一个非负整数 k,令两数中的一个数乘以 k,另一个数乘以 k^2。
请你计算,是否能够通过一系列操作,使得最终第一个数变为 a,第二个数变为 b。
输入格式
第一行包含整数 T,表示共有 T�组测试数据。
每组数据占一行,包含两个整数 a,b。
输出格式
每组数据输出一行结果,如果任务可以达成,则输出 Yes,否则输出 No。
数据范围
前 33 个测试点满足 1≤T≤5。
所有测试点满足 1≤T≤350000,1≤a,b≤10^9。
输入样例:
4
2 4
75 45
8 8
16 16
输出样例:
Yes
Yes
Yes
No二、思路(推导)
根据算术基本定理 :每个正整数都可以唯一地分成若干质数的乘积
考虑k>=2范围 ,且只需考虑k为质数的情况
p1 p2 p3 ... pn
假设用了x1个p1,x2个p2 ...xn个pn
总的操作次数=x1+x2+..+xn
次数 a b c
1 1 1
x1 p1^2 p1 p1^3 相当于有x1个p1的3次方相乘,即p1^(3*x1),以此类推
x2 p2 p2^2 p2^3
xn pn pn^2 pn^3
a*b=p1^(3x1)+p2^(3x2)+...+pn^(3xn);
1.x1<=x等价p1^x1能够整除a p1^(x1)|a x1(全分1次) <=x<=2x1(全分两次)
2.x1<=y等价p1^x1能够整除b p2^(x2)|b x1(全分1次) <=y<=2x1(全分两次)
3.x+y=3x1 x1=(x+y)/3
x:代表1变换到a所用的次数,y:代表1变换到b所用次数
若x,y在x1~2x1之间,且满足(x+y)能整除3,则说明x1有解,代表它满足条件
t=p1^(x1/3) p2(x2/3)…p3(xn/3);(pi与pj之间两两互质且独立) t就相当ab开三次方根
x1=(x+y)/3;
t=p1^(x1/3) *p2(x2/3)*...*p3(xn/3);(pi与pj之间两两互质且独立)
等价于 p1^(x1/3)|a p1^(x1/3)|b(x|y代表x能y整除,即y%x==0)
等价于 a能够被t整数 t|a t|b
即:如果 t为整数,且a%t==0&&b%t==0,则一定有解
三、代码
#include<bits/stdc++.h>
#define endl '\n'
typedef long long ll;
#define IOS ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
using namespace std;
const int N=2e5+10;
const int inf=0x3f3f3f3f;
int a,b;
void solve()
{cin>>a>>b;//int t=round(pow((LL)a*b,1.0/3));/*round(),将一个浮点数四舍五入到最接近的整数 3.4=3 3.6=4
如果参数x的小数部分>=0.5,则返回大于x的最小整数,否则返回小于x的最大整数 */ int t=pow((ll)a*b,1.0/3)+1e-8;//可能会有精度问题 if(t*(ll)t*t==(ll)a*b&&a%t==0&&b%t==0){cout<<"YES"<<endl;} else{cout<<"NO"<<endl;}
}
signed main()
{int t;cin>>t;while(t--){solve();}return 0;
} C、5287. 数量(组合数+dfs或者组合数+手动模拟)
一、题目要求
给定两个整数 n,k。
请你计算,一共有多少个长度为 n 的整数数组 a1,a2,…,an 能够同时满足:
- 数组 a 恰好是一个 1∼n的排列。
- 至少有 n−k个索引 i(1≤i≤n)满足 ai=i。
输入格式
共一行,包含两个整数 n,k。
输出格式
一个整数,表示满足条件的整数数组数量。
数据范围
前 44 个测试点满足 4≤n≤5,1≤k≤4。
所有测试点满足 4≤n≤1000,1≤k≤4。
输入样例1:
4 1
输出样例1:
1
输入样例2:
4 2
输出样例2:
7
输入样例3:
5 3
输出样例3:
31
输入样例4:
5 4
输出样例4:
76二、思路
1.思路
给出n个位置,只允许k个人不在自己的位置上,又因为k<=4,所以进行考虑的情况有k=0,2,3,4,可以手动模拟,也可以利用错排列公式。
2.错排列公式:
1.定义:考虑一个有n个元素的排列,若一个排列中所有的元素都不在自己原来的位置上,
那么这样的排列就称为原排列的一个错排。 n个元素的错排数记为D(n)
2.公式:
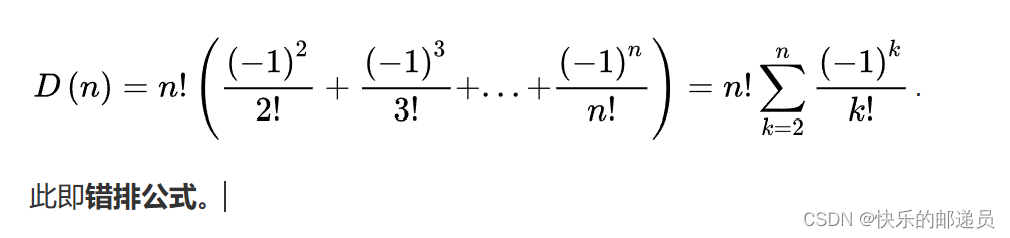


3.推导过程
ans=c(n,k)*dfs(1,k) (组合数(o(1))*dfs(o(1)))
1.k=0,则说明每个人都在自己的座位上说明只有一种情况
2.k=1,不可能只有1个人不在自己的座位上
3.k=2,c(n,2)*1
4.k=3,c(n,3)*2
1 2 3
a.2 3 1
b.3 1 2
5.k=4 c(n,4)*9
1 2 3 4
a.2 1 4 3
b.2 4 1 3
c.2 3 4 1
d.3 1 4 2
e.3 4 1 2
f.3 4 2 1
g.4 1 2 3
h.4 3 1 2
i.4 3 2 1
三、代码
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
#define IOS ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
using namespace std;
const int N=1100;
const int inf=0x3f3f3f3f;
int a[N];
int n,k;
//int path[5];
bool st[5];
int dfs(int u,int n)
{if(u>n)return 1;int res=0;for(int i=1;i<=n;i++){if(i!=u&&!st[i])//不能填自己,并且这个数没有被访问过{// patu[u]=i; st[i]=true;res+=dfs(u+1,n);//加上递归下一层的结果 st[i]=false;} }return res;
}
int c(int a,int b)
{int res=1,i,j;for(i=a,j=1;j<=b;i--,j++){res=res*i/j;}return res;
}
void solve()
{cin>>n>>k;int res=1;//c(n,0)=1 for(int i=2;i<=k;i++)//最多有k个索引不满足所以进行累加 {res+=c(n,i)*dfs(1,i);}cout<<res<<endl;
}
signed main()
{int t=1;while(t--){solve();}return 0;
}