文章目录

• 1、第 N 个泰波那契数
• 2、三步问题
• 3、使用最小花费爬楼梯
• 4、解码方法
• 5、不同路径
• 6、不同路径 II

1、第 N 个泰波那契数

泰波那契序列 Tn 定义如下：
T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2
给你整数 n，请返回第 n 个泰波那契数 Tn 的值。

class Solution {
public:int tribonacci(int n) {//状态表示vector<int> dp(n+1);//特殊情况if(n==0)return 0;if(n==1||n==2)return 1;//初始化dp[0]=0;dp[1]=dp[2]=1;for(int i=3;i<=n;i++){//状态转移方程dp[i]=dp[i-1]+dp[i-2]+dp[i-3];}return dp[n];// //空间优化// //创建三个值//     int a=0;//     int b=1;//     int c=1;//     int d=0;//     if(n==0)//         return 0;//     if(n==1||n==2)//         return 1;//     for(int i=3;i<n+1;i++)//     {//         d=a+b+c;//         a=b;//         b=c;//         c=d;//     }//     return d;}
};

2、三步问题

三步问题。有个小孩正在上楼梯，楼梯有n阶台阶，小孩一次可以上1阶、2阶或3阶。实现一种方法，计算小孩有多少种上楼梯的方式。结果可能很大，你需要对结果模1000000007。

class Solution {
public:int waysToStep(int n) {//状态表示vector<int> dp(n+1);//特殊情况处理if(n==1||n==2)return n;if(n==3)return 4;//初始化dp[1]=1,dp[2]=2,dp[3]=4;for(int i=4;i<=n;i++){dp[i]=((dp[i-1]+dp[i-2])%1000000007+dp[i-3])%1000000007;}//返回return dp[n];}
};

3、使用最小花费爬楼梯

数组的每个下标作为一个阶梯，第 i 个阶梯对应着一个非负数的体力花费值 cost[i]（下标从 0 开始）。
每当爬上一个阶梯都要花费对应的体力值，一旦支付了相应的体力值，就可以选择向上爬一个阶梯或者爬两个阶梯。
请找出达到楼层顶部的最低花费。在开始时，你可以选择从下标为 0 或 1 的元素作为初始阶梯。

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {//创建dpint n=cost.size();vector<int> dp(n+1);//初始化for(int i=2;i<=n;i++){dp[i]=min(cost[i-1]+dp[i-1],cost[i-2]+dp[i-2]);}return dp[n];}   
};

4、解码方法

class Solution {
public:int numDecodings(string s) {//创建dpint n=s.size();vector<int> dp(n);//初始化dp[0]=s[0]!='0';//处理特殊if(n==1)return dp[0];if(s[0]!='0'&&s[1]!='0') dp[1]+=1;int com=(s[0]-'0')*10+s[1]-'0';if(com>9&&com<27)dp[1]+=1;for(int i=2;i<n;i++){if(s[i]!='0') dp[i]=dp[i-1];int com=(s[i-1]-'0')*10+s[i]-'0';if(com>9&&com<27)dp[i]+=dp[i-2];   }return dp[n-1];}
};
//简化
class Solution {
public:int numDecodings(string s) {//创建dpint n=s.size();vector<int> dp(n+1);//初始化dp[0]=1;dp[1]=s[0]!='0';for(int i=2;i<=n;i++){if(s[i-1]!='0') dp[i]=dp[i-1];int com=(s[i-2]-'0')*10+s[i-1]-'0';if(com>9&&com<27)dp[i]+=dp[i-2];   }return dp[n];}
};

5、不同路径

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。
问总共有多少条不同的路径？

class Solution {
public:int uniquePaths(int m, int n) {//状态,创建dpvector<vector<int>> dp(m+1,vector<int>(n+1));//初始化dp[0][1]=1;for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){//状态转移方程dp[i][j]=dp[i-1][j]+dp[i][j-1];}}return dp[m][n];}
};

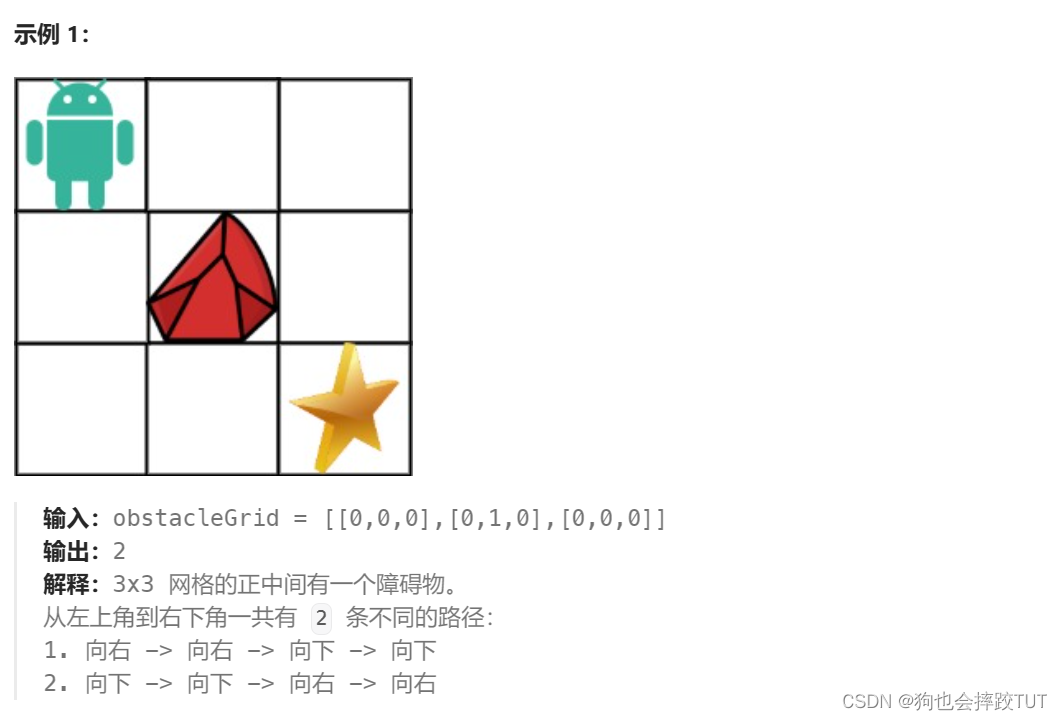
6、不同路径 II

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？
网格中的障碍物和空位置分别用 1 和 0 来表示。

class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& ob) {//创建dpint row=ob.size();int col=ob[0].size();vector<vector<int>> dp(row+1,vector<int>(col+1));//初始化dp[0][1]=1;for(int i=1;i<=row;i++){for(int j=1;j<=col;j++){if(ob[i-1][j-1]==0)dp[i][j]=dp[i-1][j]+dp[i][j-1];}}return dp[row][col];}
};